Cubic-bezier 曲线
cubic-bezier又称三次贝塞尔，主要是为animation生成速度曲线函数。
cubic-bezier(x1,y1,x2,y2)
此图中:
P0:(0,0) P1:(x1,y1) P2:(x2,y2) P3:(1,1)
（x1,x2 范围为 0-1） （y1,y2没规定，但是过大没必要也没意义。）
我对此曲线是这么理解的：假设P1，P2两个点为吸铁石，曲线是薄铁条（可以被吸铁石影响形状的那种）
那么这个曲线则是被 P1，P2两个吸铁石点拉扯形成的。
有一点需要注意，当这个点距离曲线越远，则拉扯力越大，曲线弧度越大。距离曲线越近，拉扯力越小，曲线弧度越小（这里和吸铁石相反。）
<!DOCTYPE html>
<html lang="zh-cn">
<head>
<meta charset="UTF-8">
<title>Document</title> <style>
.animation {
width: 50px;
height: 50px;
background-color: #ed3;
-webkit-transition: all 2s cubic-bezier(.17, .86, .73, .14);
-o-transition: all 2s cubic-bezier(.17, .86, .73, .14);
transition: all 2s cubic-bezier(.17, .86, .73, .14);
}
.animation:hover {
-webkit-transform: translateX(400px);
-ms-transform: translateX(400px);
-o-transform: translateX(400px);
transform: translateX(400px);
}
</style>
</head>
<body>
<div class="animation"></div>
</body>
</html>
这段代码中 (x1=0.17 y1=0.86) (x2=0.73 y2=0.14) 可以画出此运动曲线为
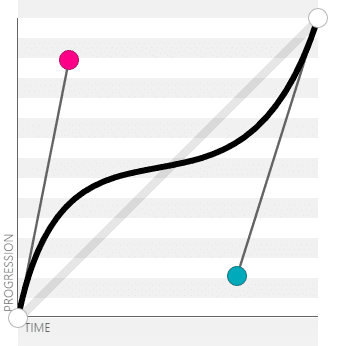
图片看不懂没关系，我教你，简单来讲可以把（0，0）当做物体的初始点，（0，1）当做物体的终点 注意这里不是（1，1），X轴从0到1为这个物体从初始点到终点的时间。
中间有段曲线大约在1/2路程的时候，发现随着时间的推移增加的很缓慢。那就说明这个物体在这段时间移动的慢。
好了，继续。下边有几个常用的曲线
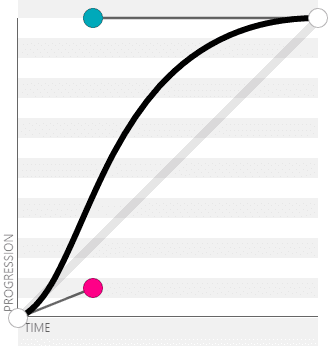
ease： cubic-bezier(.25, .1, .25, 1);
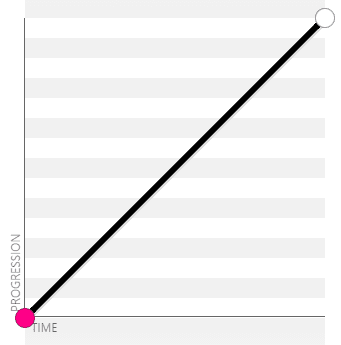
liner：cubic-bezier(0, 0, 1, 1) / cubic-bezier(1, 1, 0, 0)
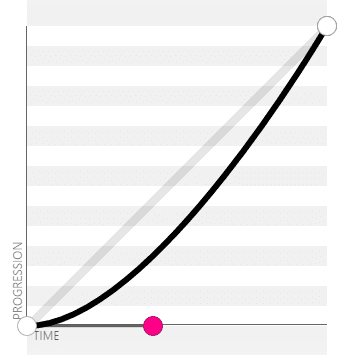
ease-in：cubic-bezier(.42, 0, 1, 1)
ease-out：cubic-bezier(0, 0, .58, 1)
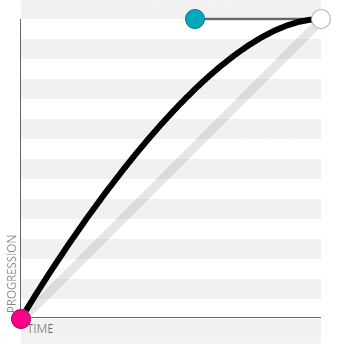
ease-in-out：cubic-bezier(.42, 0, .58, 1)
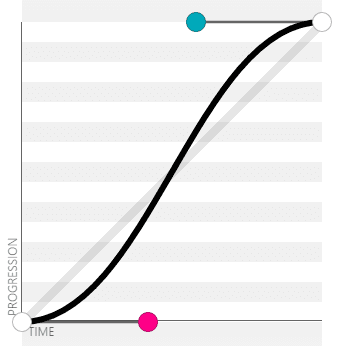
In Out . Back（来回的缓冲效果）：cubic-bezier(0.68, -0.55, 0.27, 1.55)
参考：https://www.jianshu.com/p/d999f090d333
one more thing： 这个网址可以在线创作Cubic-bezier，蛮有意思的
Cubic-bezier 曲线的更多相关文章
- Bezier曲线的原理 及 二次Bezier曲线的实现
原文地址:http://blog.csdn.net/jimi36/article/details/7792103 Bezier曲线的原理 Bezier曲线是应用于二维图形的曲线.曲线由顶点和控制点组成 ...
- [摘抄] Bezier曲线、B样条和NURBS
Bezier曲线.B样条和NURBS,NURBS是Non-Uniform Rational B-Splines的缩写,都是根据控制点来生成曲线的,那么他们有什么区别了?简单来说,就是: Bezier曲 ...
- C# 实现Bezier曲线（vs2008）
using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; usin ...
- 连续bezier曲线的实现
需求场景 一系列的坐标点,划出一条平滑的曲线 3次Bezier曲线 基本上大部分绘图工具都实现了3次Bezier曲线,4个点确定一条3次Bezier曲线.以html5中的canvas为例 let ct ...
- 7.5.5编程实例－Bezier曲线曲面绘制
(a)Bezier曲线 (b) Bezier曲面 1. 绘制Bezier曲线 #include <GL/glut.h> GLfloat ct ...
- 实验6 Bezier曲线生成
1．实验目的: 了解曲线的生成原理,掌握几种常见的曲线生成算法,利用VC+OpenGL实现Bezier曲线生成算法. 2．实验内容: (1) 结合示范代码了解曲线生成原理与算法实现,尤其是Bezier ...
- 简单而粗暴的方法画任意阶数Bezier曲线
简单而粗暴的方法画任意阶数Bezier曲线 虽然说是任意阶数,但是嘞,算法原理是可以到任意阶数,计算机大概到100多阶就会溢出了 Bezier曲线介绍] [本文代码] 背景 在windows的Open ...
- python bezier 曲线
1.手写bezier公式,生成bezier代码, 如果给的点数过多,则会生成一半bezier曲线,剩下的一半就需要进行拼接: import numpy as np import matplotlib. ...
- iOS Bezier曲线
https://www.jianshu.com/p/2316f0d9db65 1. Bezier曲线 相关软件:PaintCode:可以直接画图,软件根据图像生产Bezier曲线 相关概念:UIBez ...
- Bezier曲线的实现——de Casteljau算法
这学期同时上了计算机图形学和计算方法两门课,学到这部分的时候突然觉得de Casteljau递推算法特别像牛顿插值,尤其递推计算步骤很像牛顿差商表. 一开始用伯恩斯坦多项式计算Bezier曲线的时候, ...
随机推荐
- iOS - 苹果官方Apple Pay开发文档（中文版）- Apple Pay（1）
翻译自苹果官方Apple Pay开发文档.目前版本为1.0 概览: Apple Pay为用户从你的App里购买实际的物品和服务提供简单而安全的方法.通过Touch ID,用户可使用储存在iPhone ...
- iOS CGContextRef/UIBezierPath（绘图）
绘图的底层实现方法 注意:在drawRect方法中系统会默认创建一个上下文(C语言类型)在其他方法中不会有这样一个上下文(可以自己测试) @implementation DrawView //注意,在 ...
- BKP和RTC
Stm32内部有多个BKP寄存器,在主电源被切断或者系统产生复位的时候,BKP寄存器仍然可以利用备用电源的支持保持其重要内容. BKP在实际应用中可以存入重要数据,防止被恶意查看. BKP有入侵检测, ...
- awk 条件及循环语句和字符串函数
条件语句 if(条件表达式) 动作1 else if(条件表达式) 动作2 else 动作3 循环语句: while循环: while(条件表达式) 动作 do while循环: do 动作 whil ...
- Typora数学公式
LaTeX编辑数学公式基本语法元素 LaTeX中的数学模式有两种形式: inline 和 display. 前者是指在正文插入行间数学公式,后者独立排列,可以有或没有编号. 行间公式(inline) ...
- OAuth2在微服务架构中的应用
首先是为什么要在微服务场景使用OAuth2,这是因为使用了OAuth2后,就能向第三方系统提供授权. 其次是如何使用,见下图: 在微服务架构中使用OAuth2,有几个问题需要我们思考: 1. toke ...
- P1330 封锁阳光大学[搜索+染色]
题目来源:洛谷 题目描述 曹是一只爱刷街的老曹,暑假期间,他每天都欢快地在阳光大学的校园里刷街.河蟹看到欢快的曹,感到不爽.河蟹决定封锁阳光大学,不让曹刷街. 阳光大学的校园是一张由N个点构成的无向图 ...
- java.sql.SQLException: Access denied for user 'root'@'localhost' (using password: YES)解决方案
java.sql.SQLException: Access denied for user 'root'@'localhost' (using password: YES) at com.mysql. ...
- 小技巧：with用法 pycharm控制台输出带颜色的文字 打印进度条的
with用法 with用法在python中是一个很独特的用法,因为别的语言的中没有这个用法.所以针对这个特点我们来做一次总结,什么样的情况下可以同with 我们学到的有文件的操作,和acquire ...
- seo与python大数据结合给文本分词并提取高频词
最近研究seo和python如何结合,参考网上的一些资料,写的这个程序. 目的:分析某个行业(例如:圆柱模板)用户最关心的一些词,根据需求去自动调整TDK,以及栏目,内容页的规划 使用方法: 1.下载 ...