集成学习之Adaboost算法原理

在boosting系列算法中，Adaboost是最著名的算法之一。Adaboost既可以用作分类，也可以用作回归。

1. boosting算法基本原理

集成学习原理中，boosting系列算法的思想：

Boosting算法首先对训练集用初始权重训练一个弱学习器1，根据弱学习1的学习误差率更新训练样本点的权重，使学习误差率高的点权重变高，从而在弱学习器2得到更多重视。然后训练弱学习器2。如此重复进行，直到弱学习器到达到指定数目T，最后将T个弱学习通过集合策略整合成强学习器。

2. Adaboost算法原理

这里讲解Adaboost算法中如何解决下面4个问题：

1. 如何计算学习误差率e
2. 如何得到弱学习器权重系数α
3. 如何更新样本权重D
4. 结合策略

假设训练样本是

训练集第k个弱学习器的输出权重为

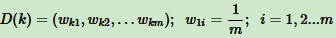
Adaboost分类问题

多元分类是二元分类的推广，假设我们是二元分类，输出为 {-1, 1}，

则第k个弱分类器 G_k(x) 在训练集上的加权误差率为

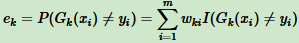
对于二分类问题，第k个弱分类器 G_k(x) 的权重系数为

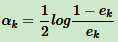
从上式看出，分类误差率 e_k 越大，对应的弱分类器权重系数 α_k 越小。即误差率小的弱分类器权重系数越大。

更新样本权重D。假设第 k 个弱分类器的样本集权重系数为 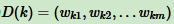，对应的第 k+1 个弱分类器的样本集权重系数为

这里 Z_k 是规范化因子

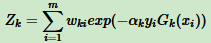
从 w_k+1,i 公式看出，如果第 i 个分类样本错误，则 ，导致样本权重在第 k+1 个弱分类器中增大，如果分类正确，则权重在第 k+1 个弱分类器中减少。