Luogu4191 [CTSC2010]性能优化【多项式，循环卷积】

题目描述：设$A,B$为$n-1$次多项式，求$A*B^C$在系数模$n+1$，长度为$n$的循环卷积。

数据范围：$n\leq 5*10^5,C\leq 10^9$，且$n$的质因子不超过7，$n+1$为质数。

---

这就是一个循环卷积，在$n=2^k$的情况下可以直接使用FFT/NTT，但是这里不行。

由于$n$的质因子很小，设$n=2^{k_1}*3^{k_2}*5^{k_3}*7^{k_4}$，我们考虑将$n$分治为$p$份（NTT就是$p=2$的情况，这里$p=2,3,5,7$）

$$F(\omega_n^i)=\sum_{i=0}^{p-1}\omega_n^iF_i(\omega_{\frac{n}{p}}^i)$$

设$a_i=F(x)[x^i]$

$$F_r(x)=\sum_{i}a_{ip+r}x^i$$

而$rev$数组其实就是把模$p$同余的放在一起。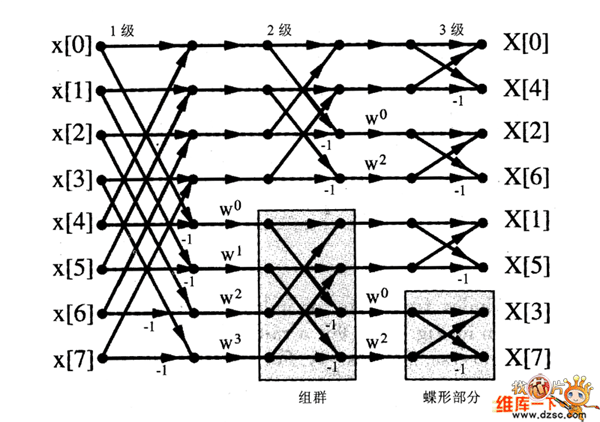

NTT的逆变换就是把次数上的$i$改成$-i$，不过代码实现里面我直接写了对$A[1:n-1]$进行reverse（这里说的就是反序）

 #include<bits/stdc++.h>
 #define Rint register int
 using namespace std;
 typedef long long LL;
 const int N = ;
 int n, C, mod, pri[N], tot, Wn[N];
 inline void add(int &a, int b){a += b; if(a >= mod) a -= mod;}
 inline int kasumi(int a, int b){
     int res = ;
     while(b){
         if(b & ) res = (LL) res * a % mod;
         a = (LL) a * a % mod;
         b >>= ;
     }
     return res;
 }
 inline void factor(int n){
     for(Rint i = ;i * i <= n;i ++)
         if(!(n % i)) pri[++ tot] = i, n /= i, -- i;
     if(n > ) pri[++ tot] = n;
 }
 inline int primitive(){
     for(Rint i = ;;i ++){
         bool flag = true;
         for(Rint j = ;j <= tot && flag;j ++)
             if(kasumi(i, n / pri[j]) == ) flag = false;
         if(flag) return i;
     }
 }
 int a[N], b[N], tmp[N];
 inline void Rev(int *A){
     for(Rint i = tot, block = n;i;block /= pri[i], i --){
         for(Rint num = , j = ;j < n;j += block)
             for(Rint k = ;k < pri[i];k ++)
                 for(Rint l = ;l < block;l += pri[i])
                     tmp[num ++] = A[j + k + l];
         for(Rint i = ;i < n;i ++) A[i] = tmp[i];
     }
 }
 inline void NTT(int *A, int type){
     Rev(A);
     for(Rint i = , block = ;i <= tot;i ++){
         int mid = block, wi = Wn[n / (block *= pri[i])];
         for(Rint j = ;j < n;j ++) tmp[j] = ;
         for(Rint j = ;j < n;j += block){
             int wk = ;
             for(Rint k = ;k < block;k ++){
                 for(Rint l = k % mid, w = ;l < block;l += mid, w = (LL) w * wk % mod)
                     add(tmp[j + k], (LL) w * A[j + l] % mod);
                 wk = (LL) wk * wi % mod;
             }
         }
         for(Rint j = ;j < n;j ++) A[j] = tmp[j];
     }
     if(type == -){
         std :: reverse(A + , A + n);
         for(Rint i = ;i < n;i ++)
             A[i] = (LL) A[i] * n % mod;
     }
 }
 int main(){
     scanf("%d%d", &n, &C); mod = n + ;
     for(Rint i = ;i < n;i ++) scanf("%d", a + i);
     for(Rint i = ;i < n;i ++) scanf("%d", b + i);
     factor(n);
     Wn[] = ; Wn[] = primitive();
     for(Rint i = ;i <= n;i ++) Wn[i] = (LL) Wn[i - ] * Wn[] % mod;
     NTT(a, ); NTT(b, );
     for(Rint i = ;i < n;i ++)
         a[i] = (LL) a[i] * kasumi(b[i], C) % mod;
     NTT(a, -);
     for(Rint i = ;i < n;i ++)
         printf("%d\n", a[i]);
 }

Luogu4191