GBDT笔记

GBDT笔记

GBDT是Boosting算法的一种，谈起提升算法我们熟悉的是Adaboost，它和AdaBoost算法不同；

区别如下： AdaBoost算法是利用前一轮的弱学习器的误差来更新样本权重值，然后一轮一轮的迭代；

GBDT也是迭代，但是GBDT要求弱学习器必须是CART模型，

而且GBDT在模型训练的时候，是要求模型预测的样本损失尽可能的小。

 

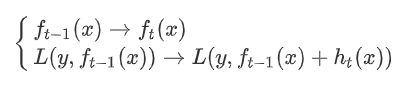
GBDT由三部分构成：

DT(Regression Decistion Tree)、GB(Gradient Boosting)和Shrinkage(衰减)

GBD是由多棵决策树组成，所有树的结果累加起来就是最终结果 迭代决策树和随机森林的区别： 随机森林使用抽取不同的样本构建不同的子树，也就是说第m棵树的构建和前m-1棵树的 结果是没有关系的 迭代决策树在构建子树的时候，使用之前子树构建结果后形成的残差作为输入数据构建下 一个子树；然后最终预测的时候按照子树构建的顺序进行预测(串行)，并将预测结果相加.

训练过程

希望损失函数能够不断的减小，并且能够尽可能快的减小。 1.让损失函数沿着梯度方向的下降。这个就是gb。 2.利用损失函数的负梯度在当前模型的值作为回归问题提升树算法中的残差的近似值去拟合一个回归树。这个是dt。 3.这样每轮训练的时候都能够让损失函数尽可能快的减小，尽快的收敛达到局部最优解或者全局最优解。

特征选择

gbdt选择特征的细节其实就是CART树生成的过程。 gbdt的弱分类器默认选择的是CART树。其实也可以选择其他弱分类器的（前提是低方差和高偏差。框架服从boosting 框架即可） CART树(是一种二叉树) 的生成：

CART树生成的过程其实就是一个选择特征的过程

1. 假设我们目前总共有 M 个特征。

2. 从中选择出一个特征 j，做为二叉树的第一个节点（选择量度为基尼系数）。

3. 对特征 j 的值选择一个切分点 m.

4. 一个样本的特征j的值如果小于m则分为一类，如果大于m则分为另外一类,如此便构建了CART 树的一个节点。

5. 其他节点的生成过程和这个是一样的迭代生成。

对于每轮选择的时候，如何选择这个特征 j,以及如何选择特征 j 的切分点 m,原始的gbdt的做法非常的暴力，首先遍历每个特征，然后对每个特征遍历它所有可能的切分点，找到最优特征 m 的最优切分点 j。

算法原理

首先给定输入向量X和输出变量Y组成的若干训练样本(X1,Y1),(X2,Y2)......(Xn,Yn)，目标是找到近似函数F(X)，使得损失函数L(Y,F(X))的损失值最小。 L损失函数一般采用最小二乘损失函数或者绝对值损失函数:

 

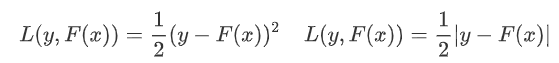
求最优解:

 

假定最终模型F(x) 是一组最优基函数f(x)的加权和:

 

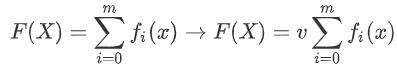
使用贪心算法的思想扩展得到Fm(X),求解最优f:

 

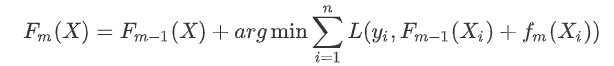
但是贪心法在每次选择最优基函数f时仍然困难，使用梯度下降的方法近似计算

给定常数函数F0(X):

 

根据梯度下降求解学习率:

 

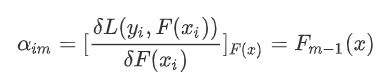
使用数据(x_i,α_im) (i=1……n )计算拟合残差找到一个CART回归树，得到第m棵树:

 

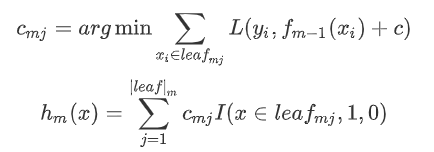
更新模型:

 

缺点:GBDT在sklearn中执行速度是最慢的

from sklearn.ensemble import GradientBoostingRegressor
​
# 使用AdaBoostRegressor; GBDT模型只支持CART模型
gbdt = GradientBoostingRegressor(n_estimators=100, learning_rate=0.01, random_state=14)
gbdt.fit(x_train, y_train)
print("训练集上R^2:%.5f" % gbdt.score(x_train, y_train))
print("测试集上R^2:%.5f" % gbdt.score(x_test, y_test))