数据结构：BF算法

贴上源代码：

#include<iostream>
using namespace std;
int BF(char S[],char T[])
{
    int i,j;
    i = j = 0;
    while(S[i]!='\0'&&T[j]!='\0'){
        if(S[i]==T[i]){
            i++;
            j++;
        }
        else{
            j = 0;
            i = i-j+1;
        }
    }
    if(T[j]=='\0')
        return i -j+1;
    else
        return 0;
}

int main()
{
    //BF
    cout<<BF("abcabcccc","abc");

    return 0;
}

这是一种低效的模式匹配算法。叫做BF算法。

主要思想十分简单：

• 给出两个字符串，分别为主串S和子串T，记下标为i，j。分别从第一个字符开始比较（即i=j=0）。当S[i]T[j]时，继续比较下一个；当S[i]!=T[j]时，j=0（重新从头开始比较子串），i的值赋为i-j+1。（关于为什么，我们接下来说）。如果S[i]'\0'了，证明主串比较完毕了，但是没有找到匹配的，即S不含有T，那么返回0；如果T[j]=='\0'了，证明子串比较完毕了，也就是主串S中含有子串T。此时返回子串T在主串S中出现的第一个字符的位置，即返回i-j+1

图示如下：

画图的时候两个串的最后都有‘\0’！！！！因为字符串的最后一位不是‘\0’么 但是我一个不小心忘了画了 也懒得改图了。。你们知道就行。。。。











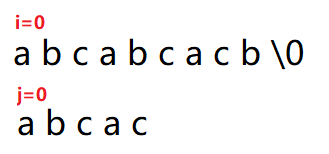
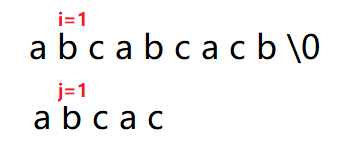
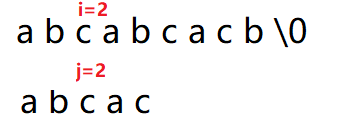
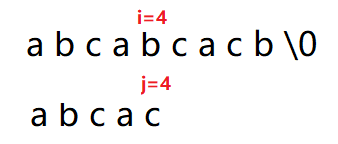
此时S[i]!=T[j]

进行“回溯”。

子串从头开始比较，主串往后挪一位开始比较。



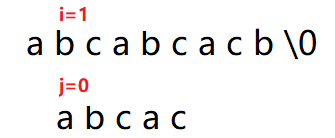
此时还是S[i]!=T[j]

进行“回溯”。

子串从头开始比较，主串往后挪一位开始比较



以此类推。。。。

即，

        if(S[i]==T[i]){
            i++;
            j++;
        }
        else{
            j = 0;
            i = i-j+1;
        }

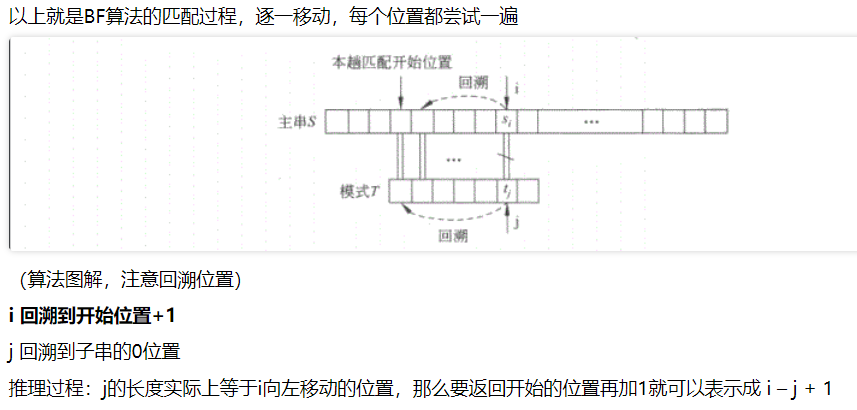
其中，i-j+1算的是i开头在的位置和j开头在的位置的差（即使i和j代表的字符相等时，同时++，也不会改变这个差）。再加上1就是再往后移一位。

依靠String实现的BF算法 C++

int BFstring(string MotherStr, string SonStr){
    int i = 0, j = 0;
    for(;(i != MotherStr.size()) && (j != SonStr.size());){
        if(MotherStr[i] == SonStr[j]){
            i++, j++;
        }
        else{
            i = i - j + 1;
            j = 0;
        }
        if(j == SonStr.size()){
            return i - j + 1;
        }

    }
    return 0;
}