PID程序实现
传统PID(位置式PID控制)调节:
这种算法的缺点是,由于全量输出,每次输出均与过去的状态有关,计算时要对
e(k) 进行累加,计算机运算工作量大。而且,因为计算机输出的 u(k) 对应的是执行机构的实际位置,如计算机出现故障, u(k) 的大幅度变化,会引起执行机构位置的大幅度变化,这种情况往往是生产实践中不允许的,在某些场合,还可能造成重大的生产事故,因而产生了增量式
PID 控制算法。
代码如下:
import matplotlib.pyplot as plt
class Pid:
def __init__(self,set_value = 100,now_value = 0,error_sum = 0,error_value = 0,error_last = 0,kp = 0,ki = 0,kd = 0):
self.set_value = set_value
self.now_value = now_value
self.error_sum = error_sum
self.error_value = error_value
self.error_last = error_last
self.kp = kp
self.ki = ki
self.kd = kd
pid = Pid(100,100,0,0,0,0.7,0.1,0.1)
data = []
i = 100
while i:
pid.error_value = pid.set_value - pid.now_value
pid.error_sum += pid.error_value
pid.now_value = pid.kp * (pid.error_value + pid.ki * pid.error_sum + pid.kd * (pid.error_value - pid.error_last))
print(pid.now_value)
data.append(pid.now_value)
pid.error_last = pid.error_value
i = i - 1
#打印输出图表的部分
plt.plot(data)
plt.title("kp=" + (str)(pid.kp) + " ki=" + (str)(pid.ki) + " kd=" + (str)(pid.kd))
plt.ylabel('output')
plt.xlabel('i')
plt.show()
波形如下(kp,ki,kd的参数需自行调节):
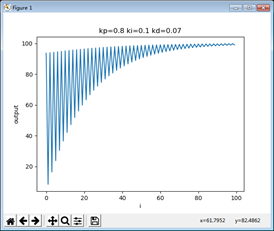
增量式PID控制调节:
代码如下:
import matplotlib.pyplot as plt
class Pid:
def __init__(self,set_value = 100,now_value = 0,add_value = 0,last_value = 0,error_value = 0,error_last = 0,error_last_last = 0,kp = 0,ki = 0,kd = 0):
self.set_value = set_value
self.now_value = now_value
self.add_value = add_value
self.last_value = last_value
self.error_value = error_value
self.error_last = error_last
self.error_last_last = error_last_last
self.kp = kp
self.ki = ki
self.kd = kd
pid = Pid(100,100,0,0,0,0,0,0.9,0.07,0.02)
data = []
i = 100
while i:
pid.error_value = pid.set_value - pid.now_value
pid.add_value = pid.kp * (pid.error_value - pid.error_last) + pid.ki * pid.error_value + pid.kd * (pid.error_value - 2 * pid.error_last + pid.error_last_last)
pid.now_value += pid.add_value
print(pid.now_value)
data.append(pid.now_value)
pid.error_last = pid.error_value
pid.error_last_last = pid.error_last
i = i - 1 plt.plot(data)
plt.title("kp=" + (str)(pid.kp) + " ki=" + (str)(pid.ki) + " kd=" + (str)(pid.kd))
plt.ylabel('output')
plt.xlabel('i')
plt.show()
波形如下((kp,ki,kd的参数需自行调节)):
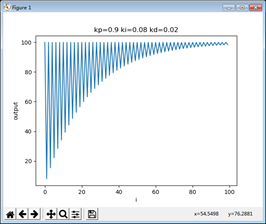
PID程序实现的更多相关文章
- 增量式PID计算公式4个疑问与理解
一开始见到PID计算公式时总是疑问为什么是那样子?为了理解那几道公式,当时将其未简化前的公式“活生生”地算了一遍,现在想来,这样的演算过程固然有助于理解,但假如一开始就带着对疑问的答案已有一定看法后再 ...
- PID控制器的数字实现及C语法讲解
PID控制器的数字实现及C语法讲解 概述 为方便学习与交流,根据自己的理解与经验写了这份教程,有错误之处请各位读者予以指出,具体包含以下三部分内容: (1) PID数字化的推导过程(实质:微积分的近 ...
- android 卸载程序、清除数据、停止服务用法
要实现卸载程序.清除数据.停止正在执行的服务这几大模块,如今将代码粗略总结例如以下: 主要运用到的类有 PackageManager ActivityManager ApplicationInfo R ...
- Android学习-应用程序管理
在前段时间,公司要求做一个Android系统的应用程序管理,要实现卸载程序.清除数据.停止正在运行的服务这几大模块,现在将代码粗略总结如下: 主要运用到的类有 PackageManager Activ ...
- linux 之程序管理
一个程序的父进程可以用PPID来判断 命令ps -l 可以用来观察程序相关的输出信息 被关闭的程序又产生:crontab或者父进程产生的 我们将常驻在系统中的程序称为:服务(daemon) ...
- Python编写守护进程程序
Python编写守护进程程序思路 1. fork子进程,父进程退出通常,我们执行服务端程序的时候都会通过终端连接到服务器,成功连接后会加载shell环境,终端和shell都是进程,shell进程是终端 ...
- perf + Flame Graph火焰图分析程序性能
1.perf命令简要介绍 性能调优时,我们通常需要分析查找到程序百分比高的热点代码片段,这便需要使用 perf record 记录单个函数级别的统计信息,并使用 perf report 来显示统计结果 ...
- [转]perf + 火焰图分析程序性能
1.perf命令简要介绍 性能调优时,我们通常需要分析查找到程序百分比高的热点代码片段,这便需要使用 perf record 记录单个函数级别的统计信息,并使用 perf report 来显示统计结果 ...
- SIMATIC PID温度控制
SIMATIC PID温度控制 // VAR_INPUT ------------------------------------------------------------------- #if ...
随机推荐
- Spark(二)CentOS7.5之Spark2.3.1HA安装
一 下载安装包 1 官方下载 官方下载地址:http://spark.apache.org/downloads.html 2 安装前提 Java8 安装成功 zookeeper 安装成功 had ...
- Python 不覆盖输入txt 读取txt
不覆盖输入: with open('1.txt','rt')as f: data=f.read() print(data+"\n") 读取txt: with open('1.txt ...
- CF1206A
CF1206A 题意: 给你 $ a , b $ 两个数组,要求从两个数组中各选一个数,使得它们的和不存在于任何一个数组. 解法: 一道极端签到的题. 因为是要构建一个不存于两个数组的数,所以直接将两 ...
- mlflow ui 启动报错No such file or directory: 'gunicorn': 'gunicorn'
1.mlflow ui 启动报错,信息如下: [root@localhost mlflow]# mlflow ui /usr/local/python3/lib/python3./importlib/ ...
- QThreadPool类和QtConcurrent命名空间
一.QThreadPool类 QThreadPool管理一组线程.它负责管理和回收单个QThread对象以减少程序中线程创建的开销.每个Qt应用程序都有一个全局的QThreadPool对象,可通过方 ...
- sqlplus 导出一张表数据
内网只让用sql developer 这软件搓的不行,数据加载到51行就黑了,没法法用sqlplus. 打开cmd, sqlplus user/passwd@ip:port/库名set colsep ...
- Java-ZipUtil
Zip 压缩工具类,不支持压缩空文件夹. 简单版 import java.io.FileOutputStream; import java.io.IOException; import java.ni ...
- MySQL中information_schema数据库是干啥的
大家在安装或使用MYSQL时,会发现除了自己安装的数据库以外,还有一个 information_schema数据库.information_schema数据库是做什么用的呢,使用WordPress博客 ...
- react hook的todolist
感觉好长时间没写博客一样,app.js代码 import React from 'react'; import { useState } from 'react'; function App() { ...
- Handler常见两种用法
1.Handler在Android的两个功能 1.1表示未来某时做某事 1.2线程间通信 2.演示源码如下: package com.example.datastrorage; import andr ...
