054. Spiral Matrix

题目链接：https://leetcode.com/problems/spiral-matrix/description/

Given a matrix of m x n elements (m rows, n columns), return all elements of the matrix in spiral order.

Example 1:

Input:
[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]
Output: [1,2,3,6,9,8,7,4,5]

Example 2:

Input:
[
  [1, 2, 3, 4],
  [5, 6, 7, 8],
  [9,10,11,12]
]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]

思路：

• 题目要求给定一个m * n的矩阵，按螺旋式的方式将其存入一个容器中
• 针对此类型的题目，其实就是找规律，最好的方法还是：观察！观察！观察！重要的事说三遍！！！
• 下面说下思路：
  • 

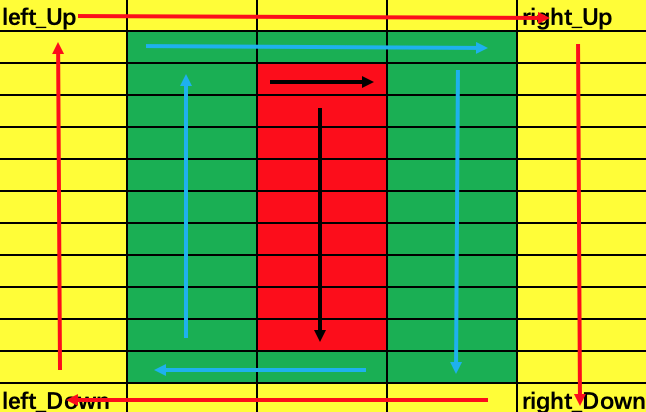
• 为了便于分析，将每次扫描矩阵边的四个角分别命名为：left_Up、right_Up、right_Down、left_Down;

• 观察可知一个完整的遍历顺序为：left_Up->right_Up->right_Down->left_Down->left_Up......，依次类推，只不过下一次遍历的范围变小了；
• 当前要解决的问题主要有如下两个：
  1. 是如何控制遍历的次数（即需要遍历几次即可遍历完整个m*n矩阵）；
  2. 每一次遍历的各个遍历方向的遍历范围如何控制。
• 通过观察发现，遍历的次数 loop = min(m, n) / 2 + min(m, n) % 2; 因为每次遍历都会遍历完成整个矩阵的两行、两列（这里的两行、两列仅仅只是指范围），而决定循环次数loop的是矩阵行数、列数中较小的那一个。
• 用（i, j）的形式表示矩阵上每一个元素的坐标（i:表示行数; j:表示列数）；i = 0， j = 0（i, j初始化为0）, m: 表示矩阵的行数，n：表示矩阵的列数 。
• 初始化：left_Up = 0, right_Up = n - j, right_Down = m - i, left_Down = 0; 矩阵从左上角left_Up开始出发
• left_Up -> right_Up的遍历过程中，即从坐标（i, left_Up）-> (i, right_Up)的过程；i不变，left_Up在变化, 令left_Up = j,  left_Up < right_Up即为循环终止条件；
• right_Up -> right_Down的遍历过程中，即从坐标(i+1, left_Up) -> (right_Down, left_Up)的过程；left_Up不变，令right_Up = i + 1, right_Up < right_Down即为循环终止条件；
• right_Down -> left_Down的遍历过程中，即从坐标(right_Up, left_Up-1) -> (right_Up, left_Down)的过程；right_up不变，令right_Down = left_Up-1, right_Dwon >= j即为循环终止条件；
• left_Down -> left_Up的遍历过程中， 即从坐标(right_Up-1, right_Down) -> (++i, right_Down)的过程；right_Down不变，令left_Down = right_Up-1, left_Down >= i即为循环终止条件；

　　注意：在循环遍历过程中也要判断元素个数，确定是否遍历完成；因为可能最后一次遍历只有四个方向的遍历（left_Up->right_Up->right_Down->left_Down->left_Up......）中的某几个方向，即一次不完整的遍历。

编码如下：

 class Solution {
 public:
     vector<int> spiralOrder(vector<vector<int>>& matrix) {
         vector<int> ivtr;
         if (matrix.size() == )
         {
             return ivtr;
         }

         int m = matrix.size();           // 矩阵行
         int n = matrix[].size();       // 矩阵列

         int i = , j = ;       // (i, j)
         int loop = min(m, n) /  + min(m, n) % ;

         while (loop-- > )
         {
             int left_Up = , right_Up = n - j, right_Down = m - i, left_Down = ;
             // 左上角到右上角遍历
             for (left_Up = j; left_Up < right_Up && ivtr.size() < m * n; ++left_Up)
             {
                 ivtr.push_back(matrix[i][left_Up]);
             }
             left_Up--;

             // 右上角到右下角遍历
             for (right_Up = i + ; right_Up < right_Down && ivtr.size() < m * n; ++right_Up)
             {
                 ivtr.push_back(matrix[right_Up][left_Up]);
             }
             right_Up--;

             // 从右下角到左下角遍历
             for (right_Down = left_Up - ; right_Down >= j && ivtr.size() < m * n; --right_Down)
             {
                 ivtr.push_back(matrix[right_Up][right_Down]);
             }
             right_Down++;

             // 从左下角到左上角遍历
             ++i;
             for (left_Down = right_Up - ; left_Down >= i && ivtr.size() < m * n; --left_Down)
             {
                 ivtr.push_back(matrix[left_Down][right_Down]);
             }
             ++j;

         }

         return ivtr;
     }
 };