数据结构-平衡二叉树 旋转过程平衡因子分析 c和java代码实现对比

平衡二叉搜索树（Self-balancing binary search tree）又被称为AVL树（有别于AVL算法），且具有以下性质：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树，同时，平衡二叉树必定是二叉排序树。

高度差可以用平衡因子bf来定义，我们用左子树的高度减去右子树的高度来表示bf，即-1<|bf|<1。

引入平衡二叉树是由于二叉排序树，在某些情况会导致树的高度一直的增加，比如一组有序的数据，在查找或创建时递归层级会很深，导致方法栈容易溢出。

平衡二叉树是通过旋转来缓解树高度增加过快的情况。

先介绍下最小不平衡节点的概念：插入一个节点之后，距离这个插入节点最近的不平衡节点就是最小不平衡节点。就是说在递归插入节点后，开始回溯，碰到的第一个不平衡的节点就是最小不平衡节点。

当最小不平衡节点右子树高则需要左旋，左子树高则需要右旋（还有些情况需要先对其左/右子树旋转）。

思考：

1、既然旋转是通过平衡因子|bf|>1来决定怎么旋转的，那么在旋转前这些平衡因子是什么时候赋值的呢？

2、旋转之后，哪些节点需要调整？，平衡因子又改如何调整呢？

下图只列出左子树高的几种情况，T表示最小不平衡节点，L表示其左子树，LR表示L的右子树，

为了形象用EH(0)，LH(1)，RH(-1)分别表示某一节点 左右子树相等、左子树高、右子树高三种情况。

根据L节点的左右子树高度差来确定直接右旋还是先左旋再右旋，因为L为最小不平衡子树的左子树，故不会出现L.bf=EH的情况。

一、L.bf=LH

右旋：

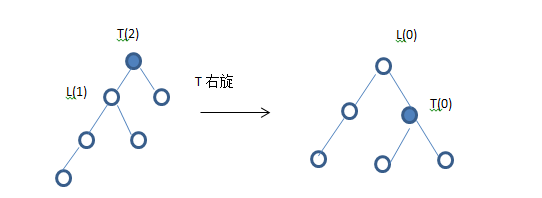
旋转之后T.bf=L.bf=EH

二、L.bf=RH

先左旋再右旋：

当L的平衡因子为-1时则需要先对L进行右旋，然后再对T进行左旋。根据LR的情况再分为下面三种（因为旋转两次，那么最后最小不平衡子树的根节点为LR，并且LR.bf=EH）

1、 LR=EH

旋转之后T.bf=L.bf=EH

2、 LR=LH

　　　　

旋转之后T.bf=RH, L.bf=EH

3、 LR=RH

　　

旋转之后T.bf=EH, L.bf=LH

我认为网上最容易懂的C语言版代码入下：

    . #include "stdio.h"
    . #include "stdlib.h"
    . #include "io.h"
    . #include "math.h"
    . #include "time.h"
    .
    . #define OK 1
    . #define ERROR 0
    . #define TRUE 1
    . #define FALSE 0
    . #define MAXSIZE 100 /* 存储空间初始分配量 */
    .
    . typedef int Status; /* Status是函数的类型,其值是函数结果状态代码，如OK等 */
    .
    .
    . /* 二叉树的二叉链表结点结构定义 */
    . typedef  struct BiTNode /* 结点结构 */
    . {
    .     int data;   /* 结点数据 */
    .     int bf; /*  结点的平衡因子 */
    .     struct BiTNode *lchild, *rchild;    /* 左右孩子指针 */
    . } BiTNode, *BiTree;
    .
    .
    . /* 对以p为根的二叉排序树作右旋处理， */
    . /* 处理之后p指向新的树根结点，即旋转处理之前的左子树的根结点 */
    . void R_Rotate(BiTree *P)
    . {
    .     BiTree L;
    .     L=(*P)->lchild; /*  L指向P的左子树根结点 */
    .     (*P)->lchild=L->rchild; /*  L的右子树挂接为P的左子树 */
    .     L->rchild=(*P);
    .     *P=L; /*  P指向新的根结点 */
    . }
    .
    . /* 对以P为根的二叉排序树作左旋处理， */
    . /* 处理之后P指向新的树根结点，即旋转处理之前的右子树的根结点0  */
    . void L_Rotate(BiTree *P)
    . {
    .     BiTree R;
    .     R=(*P)->rchild; /*  R指向P的右子树根结点 */
    .     (*P)->rchild=R->lchild; /* R的左子树挂接为P的右子树 */
    .     R->lchild=(*P);
    .     *P=R; /*  P指向新的根结点 */
    . }
    .
    . #define LH +1 /*  左高 */
    . #define EH 0  /*  等高 */
    . #define RH -1 /*  右高 */
    .
    . /*  对以指针T所指结点为根的二叉树作左平衡旋转处理 */
    . /*  本算法结束时，指针T指向新的根结点 */
    . void LeftBalance(BiTree *T)
    . {
    .     BiTree L,Lr;
    .     L=(*T)->lchild; /*  L指向T的左子树根结点 */
    .     switch(L->bf)
    .     { /*  检查T的左子树的平衡度，并作相应平衡处理 */
    .          case LH: /*  新结点插入在T的左孩子的左子树上，要作单右旋处理 */
    .             (*T)->bf=L->bf=EH;
    .             R_Rotate(T);
    .             break;
    .          case RH: /*  新结点插入在T的左孩子的右子树上，要作双旋处理 */
    .             Lr=L->rchild; /*  Lr指向T的左孩子的右子树根 */
    .             switch(Lr->bf)
    .             { /*  修改T及其左孩子的平衡因子 */
    .                 case LH: (*T)->bf=RH;
    .                          L->bf=EH;
    .                          break;
    .                 case EH: (*T)->bf=L->bf=EH;
    .                          break;
    .                 case RH: (*T)->bf=EH;
    .                          L->bf=LH;
    .                          break;
    .             }
    .             Lr->bf=EH;
    .             L_Rotate(&(*T)->lchild); /*  对T的左子树作左旋平衡处理 */
    .             R_Rotate(T); /*  对T作右旋平衡处理 */
    .     }
    . }
    .
    . /*  对以指针T所指结点为根的二叉树作右平衡旋转处理， */
    . /*  本算法结束时，指针T指向新的根结点 */
    . void RightBalance(BiTree *T)
    . {
    .     BiTree R,Rl;
    .     R=(*T)->rchild; /*  R指向T的右子树根结点 */
    .     switch(R->bf)
    .     { /*  检查T的右子树的平衡度，并作相应平衡处理 */
    .      case RH: /*  新结点插入在T的右孩子的右子树上，要作单左旋处理 */
    .               (*T)->bf=R->bf=EH;
    .               L_Rotate(T);
    .               break;
    .      case LH: /*  新结点插入在T的右孩子的左子树上，要作双旋处理 */
    .               Rl=R->lchild; /*  Rl指向T的右孩子的左子树根 */
    .               switch(Rl->bf)
    .               { /*  修改T及其右孩子的平衡因子 */
    .                 case RH: (*T)->bf=LH;
    .                          R->bf=EH;
    .                          break;
    .                 case EH: (*T)->bf=R->bf=EH;
    .                          break;
    .                 case LH: (*T)->bf=EH;
    .                          R->bf=RH;
    .                          break;
    .               }
    .               Rl->bf=EH;
    .               R_Rotate(&(*T)->rchild); /*  对T的右子树作右旋平衡处理 */
    .               L_Rotate(T); /*  对T作左旋平衡处理 */
    .     }
    . }
    .
    . /*  若在平衡的二叉排序树T中不存在和e有相同关键字的结点，则插入一个 */
    . /*  数据元素为e的新结点，并返回1，否则返回0。若因插入而使二叉排序树 */
    . /*  失去平衡，则作平衡旋转处理，布尔变量taller反映T长高与否。 */
    . Status InsertAVL(BiTree *T,int e,Status *taller)
    . {
    .     if(!*T)
    .     { /*  插入新结点，树“长高”，置taller为TRUE */
    .          *T=(BiTree)malloc(sizeof(BiTNode));
    .          (*T)->data=e; (*T)->lchild=(*T)->rchild=NULL; (*T)->bf=EH;
    .          *taller=TRUE;
    .     }
    .     else
    .     {
    .         if (e==(*T)->data)
    .         { /*  树中已存在和e有相同关键字的结点则不再插入 */
    .             *taller=FALSE; return FALSE;
    .         }
    .         if (e<(*T)->data)
    .         { /*  应继续在T的左子树中进行搜索 */
    .             if(!InsertAVL(&(*T)->lchild,e,taller)) /*  未插入 */
    .                 return FALSE;
    .             if(*taller) /*   已插入到T的左子树中且左子树“长高” */
    .                 switch((*T)->bf) /*  检查T的平衡度 */
    .                 {
    .                     case LH: /*  原本左子树比右子树高，需要作左平衡处理 */
    .                             LeftBalance(T); *taller=FALSE; break;
    .                     case EH: /*  原本左、右子树等高，现因左子树增高而使树增高 */
    .                             (*T)->bf=LH; *taller=TRUE; break;
    .                     case RH: /*  原本右子树比左子树高，现左、右子树等高 */
    .                             (*T)->bf=EH; *taller=FALSE; break;
    .                 }
    .         }
    .         else
    .         { /*  应继续在T的右子树中进行搜索 */
    .             if(!InsertAVL(&(*T)->rchild,e,taller)) /*  未插入 */
    .                 return FALSE;
    .             if(*taller) /*  已插入到T的右子树且右子树“长高” */
    .                 switch((*T)->bf) /*  检查T的平衡度 */
    .                 {
    .                     case LH: /*  原本左子树比右子树高，现左、右子树等高 */
    .                             (*T)->bf=EH; *taller=FALSE;  break;
    .                     case EH: /*  原本左、右子树等高，现因右子树增高而使树增高  */
    .                             (*T)->bf=RH; *taller=TRUE; break;
    .                     case RH: /*  原本右子树比左子树高，需要作右平衡处理 */
    .                             RightBalance(T); *taller=FALSE; break;
    .                 }
    .         }
    .     }
    .     return TRUE;
    . }
    .
    . int main(void)
    . {
    .     int i;
    .     int a[]={,,,,,,,,,};
    .     BiTree T=NULL;
    .     Status taller;
    .     for(i=;i<;i++)
    .     {
    .         InsertAVL(&T,a[i],&taller);
    .     }
    .     printf("本样例建议断点跟踪查看平衡二叉树结构");
    .     return ;
    . }  

首先整体看一遍InsertAVL函数代码，结合上面的图，我想之前两个问题都会有答案了，再重复下。

1、既然旋转是通过平衡因子|bf|>1来决定怎么旋转的，那么在旋转前这些平衡因子是什么时候赋值呢？

在元素插入之后，首先认为该元素就是一个子树，从无到有，故高度增加taller=true，然后开始回溯到上一个节点根据元素插入后，对其的三种影响来调整平衡因子，同时重新赋值taller。

2、旋转之后，哪些节点需要调整？平衡因子又改如何调整呢？

因为平衡二叉树本身也是排序树，就上图以左子树高为列，若能直接右旋，影响的节点有T、L，最后会为T.bf=L.bf=EH。

若要先左旋再右旋，则根据LR的取值再分三种情况(最后会变成LR为根，LR.bf=EH)

1、 LR.bf=EH：旋转后 T.bf=L.bf=EH

2、 LR.bf=LH：旋转后 T.bf=RH,L.bf=EH

3、 LR.bf=RH：旋转后 T.bf=EH,L.bf=LH

右子树高的情况同理。

要是你对java实现不兴趣，可以不用往下看了，数据结构主要是其思想，实现只需要根据语言特性来稍作改变。

java代码：

思路跟上面代码一样（原谅我偷懒不写注释...），主要是多了个rootAVL和preNode。原因是c语言函数传值可以直接传指针，这样对于参数的修改会反应到被调函数外面。而java都是值传递，方法内操作的只是引用的一个副本，他们指向的地址相同而已，只能修改引用所指向的内存，修改引用副本是不会影响引用本身的。

故需要单独处理节点的前驱和根节点，  rootAVL用来保存最后的根节点，因为每次插入都需要从根节点开始递归。

preNode表示每次回溯时的前面一个节点。

public class AVL {

    private boolean taller=false;
    private Node root =null;
    private static final int EH=0;
    private static final int LH=1;
    private static final int RH=-1;

    private class Node{
        public int data;
        public Node leftChild;
        public Node rightChild;
        public int balanceFactor;

        public Node(int data){
            this.data=data;
            balanceFactor=0;
        }
    }

    public  Node RRotate(Node T){
        Node temp=T.leftChild;
        T.leftChild=temp.rightChild;
        temp.rightChild=T;
        return temp;
    }

    public  Node LRotate(Node T){
        Node temp=T.rightChild;
        T.rightChild=temp.leftChild;
        temp.leftChild=T;
        return  temp;
    }

    public  Node leftBalance(Node node,Node preNode){
        Node child=node.leftChild;
        Node root=null;
        switch (child.balanceFactor){
            case LH:
                node.balanceFactor=child.balanceFactor=EH;
                root=RRotate(node);
                if(preNode!=null && node.data< preNode.data){
                    preNode.leftChild=root;
                }
                if(preNode!=null && node.data> preNode.data){
                    preNode.rightChild=root;
                }
                break;
            case RH:
                Node rchild=child.rightChild;
                switch (rchild.balanceFactor){
                    case EH:
                        node.balanceFactor=child.balanceFactor=EH;
                        break;
                    case LH:
                        node.balanceFactor=RH;
                        child.balanceFactor=EH;
                        break;
                    case RH:
                        node.balanceFactor=EH;
                        child.balanceFactor=LH;
                        break;
                    default:break;
                }
                rchild.balanceFactor=EH;
                node.leftChild=LRotate(child);
                root=RRotate(node);
                if(preNode!=null && node.data<preNode.data){
                    preNode.leftChild=root;
                }
                if(preNode!=null && node.data>preNode.data){
                    preNode.rightChild=root;
                }
                break;
            default:break;
        }
        return root;
    }

    public  Node rightBalance(Node node,Node preNode){
        Node child=node.rightChild;
        Node root=null;
        switch (child.balanceFactor){
            case RH:
                node.balanceFactor=child.balanceFactor=EH;
                root=LRotate(node);
                if(preNode!=null && node.data<preNode.data){
                    preNode.leftChild=root;
                }
                if(preNode!=null && node.data>preNode.data){
                    preNode.rightChild=root;
                }
                break;
            case LH:
                Node lchild=child.leftChild;
                switch (lchild.balanceFactor){
                    case EH:
                        node.balanceFactor=child.balanceFactor=EH;
                        break;
                    case RH:
                        node.balanceFactor=LH;
                        child.balanceFactor=EH;
                        break;
                    case LH:
                        node.balanceFactor=EH;
                        child.balanceFactor=RH;
                        break;
                    default:break;
                }
                lchild.balanceFactor=EH;
                node.rightChild=RRotate(child);
                root=LRotate(node);
                if(preNode!=null && node.data<preNode.data){
                    preNode.leftChild=root;
                }
                if( preNode!=null && node.data>preNode.data){
                    preNode.rightChild=root;
                }
                break;
            default:break;
        }
        return root;
    }

    public boolean insertNode(int value){
       return insertNode(root,value,null);
    }

    public  boolean insertNode(Node node, int value, Node preNode){
        if(node==null){
            node=new Node(value);
            node.balanceFactor=EH;
            taller=true;
            if(preNode!=null && node.data< preNode.data){
                preNode.leftChild=node;
            }
            if(preNode!=null && node.data> preNode.data){
                preNode.rightChild=node;
            }
            root =node;
            return true;
        }else{
            if(value==node.data){
                root =node;
                return false;
            }
            if (value<node.data){
                if (!insertNode(node.leftChild, value, node)) {
                    root =node;
                    return false;
                }
                if(taller){
                    switch (node.balanceFactor){
                        case EH:taller=true;node.balanceFactor=LH;break;
                        case RH:taller=false;node.balanceFactor=EH;break;
                        case LH:
                            taller=false;
                            node=leftBalance(node,preNode);
                            if(preNode!=null){
                                node=preNode;
                            }
                            break;
                        default:break;
                    }
                }
            }
            if (value>node.data){
                if (!insertNode(node.rightChild, value,node)) {
                    root =node;
                    return false;
                }
                if(taller){
                    switch (node.balanceFactor){
                        case EH:taller=true;node.balanceFactor=RH;break;
                        case LH:taller=false;node.balanceFactor=EH;break;
                        case RH:
                            taller=false;
                            node=rightBalance(node,preNode);
                            if(preNode!=null){
                                node=preNode;
                            }
                            break;
                        default:break;
                    }
                }
            }
        }
        root =node;
        return true;
    }

    public void inorderTraversal(){
        inorderTraversal(root);
    }

    public  void inorderTraversal(Node root){
        if(root!=null){
            inorderTraversal(root.leftChild);
            System.out.println("节点："+root.data+"  平衡因子："+root.balanceFactor);
            inorderTraversal(root.rightChild);
        }
        return ;
    }

    public static void main(String[] args) {
        //int[] data={8,6,4};
        //int[] data={8,6,9,5,7,3};
        //int[] data={8,6,7};
        //int[] data={8,5,9,4,6,7};
        //int[] data={8,5,9,4,7,6};
        int[] data={8,5,9,7,6};
        AVL avl=new AVL();
        for(int i=0;i<data.length;i++){
            avl.insertNode(data[i]);
        }
        avl.inorderTraversal();
    }
}