[POJ 2559]Largest Rectangle in a Histogram 题解（单调栈）

[POJ 2559]Largest Rectangle in a Histogram

Description

A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

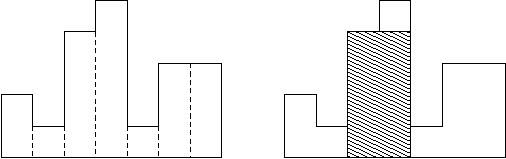
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

Input

The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1<=n<=100000. Then follow n integers h1,...,hn, where 0<=hi<=1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

Output

For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

Solution

方法一：记录左、右第一个比每个元素低的元素

1.从左往右做单增栈，弹栈时r[stack[top--]]=当前元素地址，即各个元素右侧第一个比其低的元素地址；最后清栈时站内元素的r为n+1;

2.从右往左做单增栈，弹栈时l[stack[top--]]=当前元素地址，即各个元素左侧第一个比其低的元素地址；最后清栈时站内元素的l为0;

3.对于每个元素计算其对应的最大面积max[i]=h[i]*(r[i]-l[i])，对所有max[i]取最大值即可；

鉴于本方法便于自己实现，再此不给出对应代码；

方法二：从左往右或从右往左进行一次单增栈，每次弹栈时更新最大面积

1.栈内每个单位存入两个元素：该单位高度height和对应可控宽度length，对于每个大于栈顶直接入栈的元素，stack[i].length=1；

2.对于需要先弹栈再入栈的元素，其length=弹栈所有元素length之和+1，因为被弹栈的元素的高度均≥当前元素，所以其可控范围应加上被其弹栈元素的length；

3.在弹栈过程中，记录一个temp为本次弹栈到当前为止弹出的宽度，因为为单增栈，所以每个高度均可控其后被弹栈元素的宽度，所以其对应的面积为s=temp*h[i]，取max更新ans即可；

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
struct node{
	long long height,length;
}stack[100100];
long long n,m,i,j,k,h[100100];
inline long long read(){
	long long x=0;
	bool f=true;
	char c;
	c=getchar();
	while(c<'0'||c>'9'){
		if(c=='-') f=false;
		c=getchar();
	}
	while(c>='0'&&c<='9'){
		x=(x<<1)+(x<<3)+(c^48);
		c=getchar();
	}
	return f?x:-x;
} 
void calc(){
	long long top=1,maxs=0,temp=0;
	for(i=1;i<=n;++i) h[i]=read();
	stack[1].height=h[1];
	stack[1].length=1;
	for(i=2;i<=n;++i){
		temp=0;
		while(stack[top].height>=h[i]&&top>0){
			temp+=stack[top].length;
			maxs=max(maxs,stack[top--].height*temp);
		}
		stack[++top].height=h[i];
		stack[top].length=temp+1;
	}
	temp=0;
	while(top>0){
		temp+=stack[top].length;
		maxs=max(maxs,stack[top--].height*temp);
	}
	printf("%lld\n",maxs);
	return;
}
int main(){
	for(;;){
		n=read();
		if(!n)return 0;
		calc();
	}
	return 0;
}

单调栈基础知识部分可以参考我的题解：http://www.cnblogs.com/COLIN-LIGHTNING/p/8474668.html