python kd树 搜索 代码

　　kd树就是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构，可以运用在k近邻法中，实现快速k近邻搜索。构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分，依次选择坐标轴对空间进行切分，选择训练实例点在选定坐标轴上的中位数为切分点。具体kd树的原理可以参考kd树的原理。

　　代码是参考《统计学习方法》k近邻 kd树的python实现得到

　　首先创建一个类，用于表示树的节点，包括：该节点的值，用于划分左右子树的切分轴，左子树，右子树

class decisionnode:
    def __init__(self,value=None,col=None,rb=None,lb=None):
        self.value=value
        self.col=col
        self.rb=rb
        self.lb=lb

　　切分点为坐标轴上的中值，下面代码求得一个序列的中值

def median(x):
    n=len(x)
    x=list(x)
    x_order=sorted(x)
    return x_order[n//2],x.index(x_order[n//2])

然后就可以构造一颗kd树，左子树小于切分点，右子树大于切分点，data是输入的数据

def buildtree(x,j=0):
    rb=[]
    lb=[]
    m,n=x.shape
    if m==0: return None
    edge,row=median(x[:,j].copy())
    for i in range(m):
        if x[i][j]>edge:
            rb.append(i)
        if x[i][j]<edge:
            lb.append(i)
    rb_x=x[rb,:]
    lb_x=x[lb,:]
    rightBranch=buildtree(rb_x,(j+1)%n)
    leftBranch=buildtree(lb_x,(j+1)%n)
    return decisionnode(x[row,:],j,rightBranch,leftBranch)

　　接下来是树的搜索过程，可以用下图表示树的搜索过程，具体过程可以参考kd树的原理。

　　

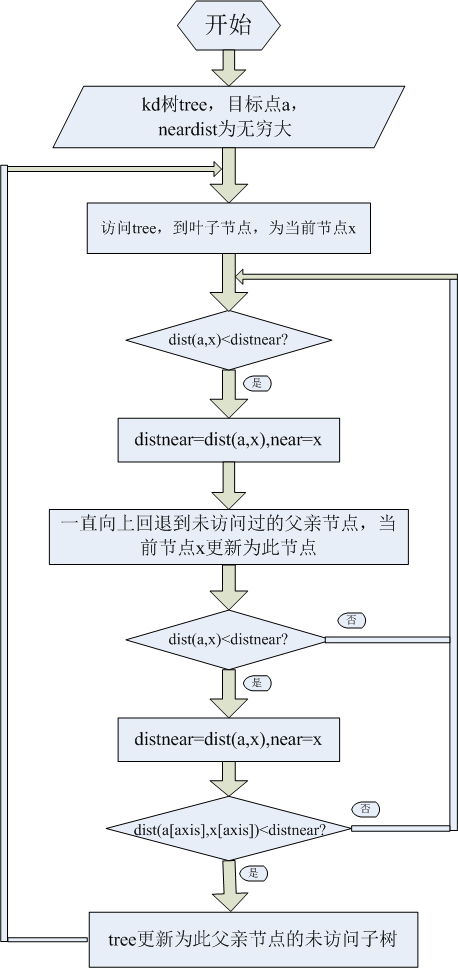
　　代码如下：

#搜索树：nearestPoint,nearestValue均为全局变量
def traveltree(node,point):
    global nearestPoint,nearestValue
    if node==None: return
    print(node.value)
    print('---')
    col=node.col
    if point[col]>node.value[col]:
        traveltree(node.rb,point)
    if point[col]<node.value[col]:
        traveltree(node.lb,point)
    dis=dist(node.value,point)
    print(dis)
    if dis<nearestValue:
        nearestPoint=node
        nearestValue=dis
        #print('nearestPoint,nearestValue' % (nearestPoint,nearestValue))
    if node.rb!=None or node.lb!=None:
        if abs(point[node.col] - node.value[node.col]) < nearestValue:
            if point[node.col]<node.value[node.col]:
                traveltree(node.rb,point)
            if point[node.col]>node.value[node.col]:
                traveltree(node.lb,point)

def searchtree(tree,aim):
    global nearestPoint,nearestValue
    #nearestPoint=None
    nearestValue=float('inf')
    traveltree(tree,aim)
    return nearestPoint

def dist(x1, x2): #欧式距离的计算
    return ((np.array(x1) - np.array(x2)) ** 2).sum() ** 0.5

 完整代码在此处取

 import numpy as np
 from numpy import array
 class decisionnode:
     def __init__(self,value=None,col=None,rb=None,lb=None):
         self.value=value
         self.col=col
         self.rb=rb
         self.lb=lb

 #读取数据并将数据转换为矩阵形式
 def readdata(filename):
     data=open(filename).readlines()
     x=[]
     for line in data:
         line=line.strip().split('\t')
         x_i=[]
         for num in line:
             num=float(num)
             x_i.append(num)
         x.append(x_i)
     x=array(x)
     return x

 #求序列的中值
 def median(x):
     n=len(x)
     x=list(x)
     x_order=sorted(x)
     return x_order[n//2],x.index(x_order[n//2])

 #以j列的中值划分数据，左小右大，j=节点深度%列数
 def buildtree(x,j=0):
     rb=[]
     lb=[]
     m,n=x.shape
     if m==0: return None
     edge,row=median(x[:,j].copy())
     for i in range(m):
         if x[i][j]>edge:
             rb.append(i)
         if x[i][j]<edge:
             lb.append(i)
     rb_x=x[rb,:]
     lb_x=x[lb,:]
     rightBranch=buildtree(rb_x,(j+1)%n)
     leftBranch=buildtree(lb_x,(j+1)%n)
     return decisionnode(x[row,:],j,rightBranch,leftBranch)

 #搜索树：nearestPoint,nearestValue均为全局变量
 def traveltree(node,point):
     global nearestPoint,nearestValue
     if node==None: return
     print(node.value)
     print('---')
     col=node.col
     if point[col]>node.value[col]:
         traveltree(node.rb,point)
     if point[col]<node.value[col]:
         traveltree(node.lb,point)
     dis=dist(node.value,point)
     print(dis)
     if dis<nearestValue:
         nearestPoint=node
         nearestValue=dis
         #print('nearestPoint,nearestValue' % (nearestPoint,nearestValue))
     if node.rb!=None or node.lb!=None:
         if abs(point[node.col] - node.value[node.col]) < nearestValue:
             if point[node.col]<node.value[node.col]:
                 traveltree(node.rb,point)
             if point[node.col]>node.value[node.col]:
                 traveltree(node.lb,point)

 def searchtree(tree,aim):
     global nearestPoint,nearestValue
     #nearestPoint=None
     nearestValue=float('inf')
     traveltree(tree,aim)
     return nearestPoint

 def dist(x1, x2): #欧式距离的计算
     return ((np.array(x1) - np.array(x2)) ** 2).sum() ** 0.5  

kdtree