POJ3450 Corporate Identity
后缀数组。
解决多个字符串的最长公共子串。
采用对长度的二分,将子串按height分组,每次判断是否在每个字符串中都出现过。
复杂度O(NlogN)
By:大奕哥
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<iostream>
#define rank fank
using namespace std;
const int N=;
int r[N],wa[N],wb[N],wv[N],wu[N],sa[N],rank[N],height[N],bel[N],cnt;
int cmp(int *r,int a,int b,int l)
{
return r[a]==r[b]&&r[a+l]==r[b+l];
}
void da(int *r,int *sa,int n,int m)
{
int i,j,p;int *x=wa,*y=wb;
for(i=;i<m;++i)wu[i]=;
for(i=;i<n;++i)wu[x[i]=r[i]]++;
for(i=;i<m;++i)wu[i]+=wu[i-];
for(i=n-;i>=;--i)sa[--wu[x[i]]]=i;
for(j=,p=;p<n;j<<=,m=p)
{
for(p=,i=n-j;i<n;++i)y[p++]=i;
for(i=;i<n;++i)if(sa[i]>=j)y[p++]=sa[i]-j;
for(i=;i<n;++i)wv[i]=x[y[i]];
for(i=;i<m;++i)wu[i]=;
for(i=;i<n;++i)wu[wv[i]]++;
for(i=;i<m;++i)wu[i]+=wu[i-];
for(i=n-;i>=;--i)sa[--wu[wv[i]]]=y[i];
for(swap(x,y),p=,x[sa[]]=,i=;i<n;++i)
x[sa[i]]=cmp(y,sa[i-],sa[i],j)?p-:p++;
}
return;
}
void calcHeight(int *rank,int *sa,int n)
{
int i,j,k=;
for(i=;i<=n;++i)rank[sa[i]]=i;
for(i=;i<n;height[rank[i++]]=k)
for(k?k--:,j=sa[rank[i]-];r[i+k]==r[j+k];++k);
return ;
}
char s[N],ans[N];
bool v[];
int tot,num;
bool check(int x,int n)
{
memset(v,,sizeof(v));
for(int i=;i<=n;++i)
{
if(height[i]<x){cnt=;memset(v,,sizeof(v));}
else
{
if(v[bel[sa[i-]]]==){
cnt++;v[bel[sa[i-]]]=;
}
if(v[bel[sa[i]]]==){
cnt++;v[bel[sa[i]]]=;
}
if(cnt==num)
{
for(int j=;j<x;++j)
ans[j]=r[sa[i]+j];
ans[x]='\0';
return ;
}
}
}
return ;
}
int main()
{
while(~scanf("%d",&num)&&num)
{
int len=;
for(int i=;i<num;++i)
{
scanf("%s",s);
int n=strlen(s);
for(int j=;j<n;++j)
{
r[len]=s[j];bel[len]=i;++len;
}
r[len]=+i;bel[len]=+i;++len;
}
--len;r[len]=;
da(r,sa,len+,);
calcHeight(rank,sa,len);
int as=,l=,r=len;
while(l<=r)
{
int mid=l+r>>;
if(check(mid,len))as=,l=mid+;
else r=mid-;
}
if(as)printf("%s\n",ans);
else
printf("IDENTITY LOST\n");
}
return ;
}
Ps:wa了好多遍,因为插进去的ascII码值没有选好,附一张ascII表。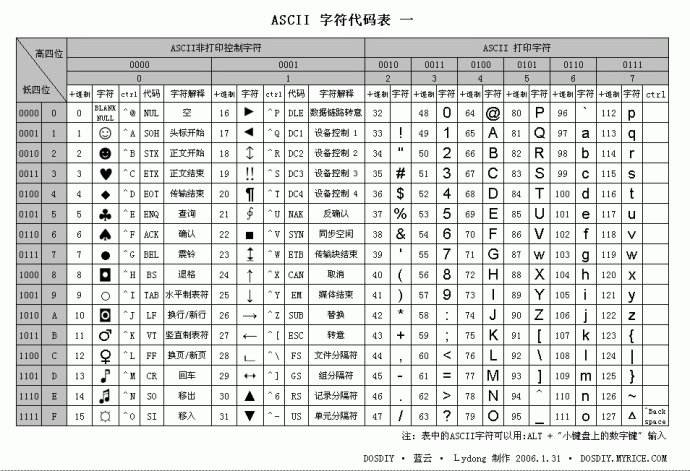
POJ3450 Corporate Identity的更多相关文章
- POJ3450 Corporate Identity —— 后缀数组 最长公共子序列
题目链接:https://vjudge.net/problem/POJ-3450 Corporate Identity Time Limit: 3000MS Memory Limit: 65536 ...
- POJ-3450 Corporate Identity (KMP+后缀数组)
Description Beside other services, ACM helps companies to clearly state their “corporate identity”, ...
- POJ3450 Corporate Identity 【后缀数组】
Corporate Identity Time Limit: 3000MS Memory Limit: 65536K Total Submissions: 7662 Accepted: 264 ...
- [poj3450]Corporate Identity(后缀数组)
题意:多个字符串的最长公共子串. 解题关键:字符串的任何一个子串都是这个字符串的某个后缀的前缀.求A和B的最长公共子串等价于求A的后缀和B的后缀的最长公共前缀的最大值. 后缀数组的经典例题,连接在一起 ...
- hdu 2328 Corporate Identity(kmp)
Problem Description Beside other services, ACM helps companies to clearly state their “corporate ide ...
- hdu2328 Corporate Identity【string库使用】【暴力】【KMP】
Corporate Identity Time Limit: 9000/3000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Other ...
- hdu2328 Corporate Identity 扩展KMP
Beside other services, ACM helps companies to clearly state their “corporate identity”, which includ ...
- (KMP 暴力)Corporate Identity -- hdu -- 2328
http://acm.hdu.edu.cn/showproblem.php?pid=2328 Corporate Identity Time Limit: 9000/3000 MS (Java/Oth ...
- hdu2328 Corporate Identity
地址:http://acm.hdu.edu.cn/showproblem.php?pid=2328 题目: Corporate Identity Time Limit: 9000/3000 MS (J ...
随机推荐
- 【CodeForces】960 F. Pathwalks 主席树+动态规划
[题目]F. Pathwalks [题意]给定n个点m条边的有向图,可能不连通有重边有自环.每条边有编号 i 和边权 wi ,求最长的路径(可以经过重复节点)满足编号和边权都严格递增.n,m,wi&l ...
- flume监控一个linux指定的一个文件夹的文件信息
1.编辑一个配置文件 flume-app.conf 拷贝至fulme的安装目录的conf下 # The configuration file needs to define the sources, ...
- python-cookbook读书笔记
今天开始读<python-cookbook>,书里有许多python优雅的写法,可以作为python的一本进阶书. 感谢译者.项目地址: https://github.com/yidao6 ...
- 使用OpenCV和Python进行人脸识别
介绍 人脸识别是什么?或识别是什么?当你看到一个苹果时,你的大脑会立刻告诉你这是一个苹果.在这个过程中,你的大脑告诉你这是一个苹果水果,用简单的语言来说就是识别.那么什么是人脸识别呢?我肯定你猜对了. ...
- eclipse启动项目
今天做的任务不多,没有自己写代码,上午看了些文章,下午我司后台给配了配项目环境,全装C盘了..以后有我好受的.. 看着后台操作,修改了N多配置,tomcat.redis.zkServer..Nginx ...
- unity3d 资源文件从MAX或者MAYA中导出的注意事项
unity3d 资源文件从MAX或者MAYA中导出的注意事项 1.首先,Unity3d 中,导出带动画的资源有2种导出方式可以选择: 1) 导出资源时,只导出一个文件,保留模型,骨骼和所 ...
- python3爬虫.4.下载煎蛋网妹子图
开始我学习爬虫的目标 ----> 煎蛋网 通过设置User-Agent获取网页,发现本该是图片链接的地方被一个js函数代替了 于是全局搜索到该函数 function jandan_load_im ...
- AngularJS 指令绑定 & 简介
指令中独立scope 的 & 官方说明: 1. 绑定表达式 2. 经常用来绑定回调函数 诡异的地方在于,这个 & 某次听人说在子组件中是不能传值给callback的,好奇查了一下官方文 ...
- [ python ] 面向对象 - 选课系统
根据源程序进行改写: 原程序地址:http://www.cnblogs.com/lianzhilei/p/5985333.html 如有侵权立即删除. 感谢原作者将完整的代码提供参考. ...
- golang-goroutine和channel
goroutine 在go语言中,每一个并发的执行单元叫做一个goroutine 这里说到并发,所以先解释一下并发和并行的概念: 并发:逻辑上具备同时处理多个任务的能力 并行:物理上在同一时刻执行多个 ...
