【2018.06.26NOIP模拟】T3节目parade

题目描述

学校一年一度的学生艺术节开始啦！在这次的艺术节上总共有 N 个节目，并且总共也有 N 个舞台供大家表演。其中第 i 个节目的表演时间为第 i 个单位时间，表演的舞台为 Ai ，注意可能有多个节目使用同一个舞台。作为 Tom 的忠实粉丝之一的 Alice，当然要来逛一下啦，顺便看一下能不能要到 Tom 的签名。

Alice 一开始会先在 A1 看完节目1再去闲逛。

Alice 可以在舞台之间随便乱走。但是假如 Alice 当前在看第 i 个节目，站在第 Ai 个舞台前面的话，由于有些道路被封锁了，所以Alice 下一步只能前往第 Li～Ri 个舞台中的一个。并且当一个节目结束的时候，Alice 只能去看另外一个节目，或者结束自己的闲逛。

具体而言就是说，假设 Alice 可以从第 i 个节目走去第 j 个节目，那么当且仅当i<j" role="presentation">i<ji<j且Li≤Aj≤Ri" role="presentation">Li≤Aj≤RiLi≤Aj≤Ri。

但事实上是，Tom 非常讨厌被自己的粉丝跟踪。所以他想在只封锁掉一个节目的情况下，使得 Alice 不能到达自己所在的地方。并且为了防止意外，他还想知道有多少个这样的节目。

简而言之，Tom 想知道对于任意一个节目 p∈[1,N] ，有多少个节目 t ，使得删掉 t 之后，不存在一条从节目1 出发到节目p 的路径。注意，节目1 和节目p 也是可以被删的。由于他非常的忙碌，所以他把这个任务交给了你。

输入格式

第一行包括一个正整数 N ，表示总共有 N 个节目。

第二行包括 N 个正整数 Ai ，表示第 i 个节目占用了第 Ai 个舞台。

接下来的 N 行，第 i 行包括两个正整数 Li，Ri，表示第 i 个节目的路径限制。

输出格式

总共 N 行。第 i 行包括一个整数 c ，表示当 Tom 站在第 i 个节目的时候，有多少个满足要求的节点。

特别的，若一开始就不存在从 1 出发到 i 的路径的话，你需要输出 -1 。

输入

10

1 6 1 8 7 2 3 9 10 10

5 8

2 4

1 2

9 10

8 9

9 9

10 10

2 2

2 4

9 9

输出

1

2

-1

2

2

3

3

2

2

2

备注

【样例解释】

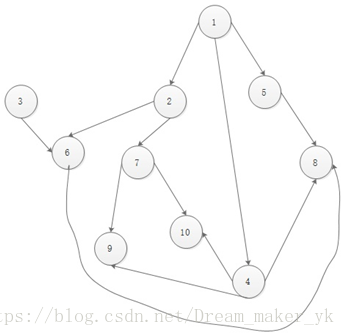
我们假如将一个节目视为一个节点的话，按题意所述，我们可以构造出一副有向图。

设对于点i，他可选的删除集合为 Si，那么很直观的就可以看出来：

对于1号节点，S1 = {1}

对于2号节点，S2 = {1，2}

对于3号节点，由于本来就不存在 1 到 3 的路径，所以应输出 -1

对于4号节点，S4 = {1，4}

对于5号节点，S5 = {1，5}

对于6号节点，S6 = {1，2，6}

对于7号节点，S7 = {1，2，7}

对于8号节点，S8 = {1，8}，5 号点和 6 号点都不是合法的点。

对于9号节点，S9 = {1，9}

对于10号节点，S10 = {1，10}

【数据范围】

对于 15% 的数据，N≤100

对于 30% 的数据，N≤800

对于 50% 的数据，N≤5000

对于 70% 的数据，N≤10000

对于 100% 的数据，N≤50000

考试的时候果断写了一个O(n2)" role="presentation">O(n2)O(n2)的暴力搞到了30分，但是看正解什么Dominator Tree内心是炸裂的，后面仔细研究了一下标程，大概搞懂了是什么意思

我们可以希望处理出1到一个点的路径上的所有必经点，那么我们记录一下到一个点i上的距离i的最近必经点idom，所以对于一个i答案就是路径上所有节点的最近必经点的并集，又因为idom是i在dominator tree上的所有祖先的集合（dominator tree根据必须经过关系建树），所以idim就是在路径上所有点在dominator tree上的LCA，然后我们就可以用top排序跑一边就好了，然后我们就可以O((N+E)log(N))" role="presentation">O((N+E)log(N))O((N+E)log(N))得到答案，其中N和E分别为Dag中的点数和边数

然后考虑原题中的(Li,Ri)" role="presentation">(Li,Ri)(Li,Ri)限制，然后我们可以建立一颗线段树，那我们考虑怎么对题目要求的关系进行构图，设线段树Ti" role="presentation">TiTi的一个区间储存了i<=j,L<=Aj<=R" role="presentation">i<=j,L<=Aj<=Ri<=j,L<=Aj<=R的点集Si,Li,Ri" role="presentation">Si,Li,RiSi,Li,Ri，那么对于一个新的点i，相当于连到了Ti+1" role="presentation">Ti+1Ti+1中(Li,Ri)" role="presentation">(Li,Ri)(Li,Ri)的所有点，那么我们对于每一个新的节点，我们建立节点Pi,Li,Ri" role="presentation">Pi,Li,RiPi,Li,Ri，并且让P连接到S集合中的所有点，那么我们考虑i号节点，我们在线段树中将(Li,Ri)" role="presentation">(Li,Ri)(Li,Ri)拆分成若干个区间(lj,rj)" role="presentation">(lj,rj)(lj,rj)那么我们只需要把Pi,Li,Ri" role="presentation">Pi,Li,RiPi,Li,Ri连接到Pi+1,lj,rj" role="presentation">Pi+1,lj,rjPi+1,lj,rj，这样维护显然原图联通关系并不会受到影响。

那么考虑怎么维护所有的T，显然，如果使用静态储存方式，我们肯定会MLE，所以我们采取可持久化线段树的思想，进行维护。

那么假如现在要向Ti,L,R" role="presentation">Ti,L,RTi,L,R中加入一个j，那么我们需要把Pi,L,R" role="presentation">Pi,L,RPi,L,R连接到j，同样的，我们还需要把Pi,L,R" role="presentation">Pi,L,RPi,L,R连接到剩下的属于Si,L,R" role="presentation">Si,L,RSi,L,R的节点，又因为我们可以发现Si,L,R−Si+1,L,R=j" role="presentation">Si,L,R−Si+1,L,R=jSi,L,R−Si+1,L,R=j所以我们只需要把Pi,L,R" role="presentation">Pi,L,RPi,L,R连接到Pi+1,L,R" role="presentation">Pi+1,L,RPi+1,L,R

那么我们就可以发现原Dag中的连通性是不会改变的

来分析一下时间复杂度：

原图中有n个点，对于每个点建线段树的时候我们只会加入log(n)" role="presentation">log(n)log(n)个点，所以点数只有nlog(n)" role="presentation">nlog(n)nlog(n)个，同样的，我们发现对于每一个点建树时只会增加2log(n)" role="presentation">2log(n)2log(n)条边，所以总边数是nlog(n)" role="presentation">nlog(n)nlog(n)规模的，按照dominator tree的时间复杂度，我们发现这道题的总复杂度是O((nlogn)log(nlogn))" role="presentation">O((nlogn)log(nlogn))O((nlogn)log(nlogn))

还有就是跑lca的时候边界写挂了，下次应该注意边界问题

#include<bits/stdc++.h>

using namespace std;

#define N 1000010

int n,ind=0;

int a[N],l[N],r[N],rt[N];

struct Node{int l,r;}t[N];

struct Edge{int v,next;};

struct Dominator_Tree{

    bool vis[N];

    int head[N],tot;

    int fa[N][31],dep[N];

    int ans[N],cnt[N];

    Edge E[N<<1];

    void add(int u,int v){

        E[++tot]=(Edge){v,head[u]};

        head[u]=tot;

    }

//  int lca(int x,int y){

//      if(dep[x]<dep[y])swap(x,y);

//      int t=dep[x]-dep[y];

//      for(int i=30;i;i--)

//          if(t&(1<<i))x=fa[x][i];

//      if(x==y)return x;

//      for(int i=30;i>=0;i--)

//          if(fa[x][i]!=fa[y][i])

//              x=fa[x][i],y=fa[y][i];

//      return fa[x][0];

//  }

    int lca(int x,int y) {

        if(dep[x]<dep[y])swap(x,y);

        int t=dep[x]-dep[y];

        for(int i=30;i>=0;i--)

            if(t&(1<<i))x=fa[x][i];

        if(x==y)return x;

        for(int i=30;i>=0;i--)

            if(fa[x][i]!=fa[y][i])

                x=fa[x][i],y=fa[y][i];

        return fa[x][0];

    }

    void bfs(){

        memset(cnt,0,sizeof(cnt));

        queue<int> q;q.push(1);

        vis[1]=1;

        while(!q.empty()){

            int u=q.front();q.pop();

            for(int i=head[u];i;i=E[i].next){

                int v=E[i].v;

                cnt[v]++;

                if(!vis[v]){

                    vis[v]=1;

                    q.push(v);

                }

            }

        }

    }

    void work(){

        bfs();

        stack<int> s;

        s.push(1);

        while(!s.empty()){

            int u=s.top();s.pop();

            dep[u]=dep[fa[u][0]]+1;

            ans[u]=ans[fa[u][0]]+(u<=n);

            for(int i=1;i<=30;i++)

                fa[u][i]=fa[fa[u][i-1]][i-1];

            for(int i=head[u];i;i=E[i].next){

                int v=E[i].v;

                if(!fa[v][0])fa[v][0]=u;

                else fa[v][0]=lca(fa[v][0],u);

                if(!(--cnt[v]))s.push(v);

            }

        }

        for(int i=1;i<=n;i++)

            if(dep[i])printf("%d\n",ans[i]);

            else printf("-1\n");

    }

}dominator_tree;

void add_edge(int x,int ll,int rr,int L,int R,int las){

    if(!las)return;

    if(R<ll||L>rr)return;

    if(L<=ll&&rr<=R){dominator_tree.add(x,las+n);return;}

    int mid=(ll+rr)>>1;

    add_edge(x,ll,mid,L,R,t[las].l);

    add_edge(x,mid+1,rr,L,R,t[las].r);

}

int add_point(int ll,int rr,int pos,int las,int v){

    int tmp=++ind;

    t[tmp]=t[las];

    if(las)dominator_tree.add(tmp+n,las+n);

    dominator_tree.add(tmp+n,v);

    if(ll==rr)return tmp;

    int mid=(ll+rr)>>1;

    if(pos<=mid)t[tmp].l=add_point(ll,mid,pos,t[las].l,v);

    else t[tmp].r=add_point(mid+1,rr,pos,t[las].r,v);

    return tmp;

}

int main(){

//  freopen("parade.in","r",stdin);

//  freopen("parade.out","w",stdout);

    scanf("%d",&n);

    for(int i=1;i<=n;i++)scanf("%d",&a[i]);

    for(int i=1;i<=n;i++)scanf("%d%d",&l[i],&r[i]);

    for(int i=n;i;i--){

        add_edge(i,1,n,l[i],r[i],rt[i+1]);

        rt[i]=add_point(1,n,a[i],rt[i+1],i);

    }

    dominator_tree.work();

    return 0;

}