codeforces 981 C.Useful Decomposition

C. Useful Decomposition

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Ramesses knows a lot about problems involving trees (undirected connected graphs without cycles)!

He created a new useful tree decomposition, but he does not know how to construct it, so he asked you for help!

The decomposition is the splitting the edges of the tree in some simple paths in such a way that each two paths have at least one common vertex. Each edge of the tree should be in exactly one path.

Help Remesses, find such a decomposition of the tree or derermine that there is no such decomposition.

Input

The first line contains a single integer $$$n$$$ ($$$2 \leq n \leq 10^{5}$$$) the number of nodes in the tree.

Each of the next $$$n - 1$$$ lines contains two integers $$$a_i$$$ and $$$b_i$$$ ($$$1 \leq a_i, b_i \leq n$$$, $$$a_i \neq b_i$$$) — the edges of the tree. It is guaranteed that the given edges form a tree.

Output

If there are no decompositions, print the only line containing "No".

Otherwise in the first line print "Yes", and in the second line print the number of paths in the decomposition $$$m$$$.

Each of the next $$$m$$$ lines should contain two integers $$$u_i$$$, $$$v_i$$$ ($$$1 \leq u_i, v_i \leq n$$$, $$$u_i \neq v_i$$$) denoting that one of the paths in the decomposition is the simple path between nodes $$$u_i$$$ and $$$v_i$$$.

Each pair of paths in the decomposition should have at least one common vertex, and each edge of the tree should be presented in exactly one path. You can print the paths and the ends of each path in arbitrary order.

If there are multiple decompositions, print any.

Examples

Input

4
1 2
2 3
3 4

Output

Yes
1
1 4

Input

6
1 2
2 3
3 4
2 5
3 6

Output

No

Input

5
1 2
1 3
1 4
1 5

Output

Yes
4
1 2
1 3
1 4
1 5

Note

The tree from the first example is shown on the picture below: 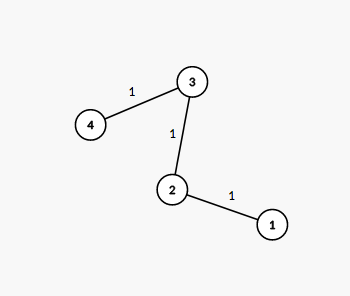The number next to each edge corresponds to the path number in the decomposition. It is easy to see that this decomposition suits the required conditions.

The tree from the second example is shown on the picture below: 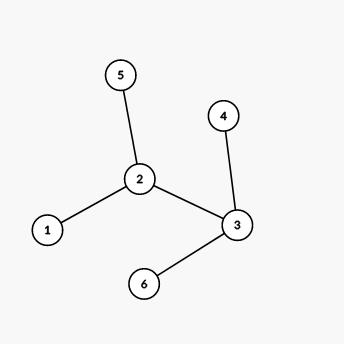We can show that there are no valid decompositions of this tree.

The tree from the third example is shown on the picture below: 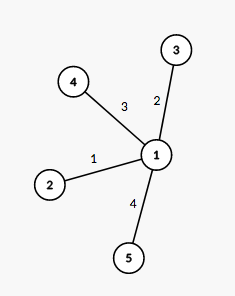The number next to each edge corresponds to the path number in the decomposition. It is easy to see that this decomposition suits the required conditions.

【题意】
给一个无向边的树，要求拆成若干条简单路径，并且这些路径都经过一个公共点。给出任意一个解决方案，如不存在输出No。

【分析】
所有的路径都有公共点，如果解决方案存在的话，那么倒着推回去，把公共点看成根节点，这棵树一定是所有的路径都从根结点出发，且都不分叉的，因为在满足这个性质时才能拆分，如果不满足，则一定有一条路径不经过根节点。
所以检查一棵树能否拆分，只用检查分叉点是否唯一就行了。而拆下来的路径，一端一定是根结点，而另一端就是这个树的所有叶子结点。

【代码】

#include<stdio.h>
#define N_max 100005

int cnt[N_max] = { 0 };//记录所有点的度数
int end[N_max] = { 0 }, ne=0;//记录所有端点序号

int main() {
	int n;
	scanf("%d", &n);
	int a1, a2;
	for (int i = 0; i < n - 1; ++i) {
		scanf("%d %d", &a1, &a2);
		cnt[a1]++;
		cnt[a2]++;
	}
	//检查分叉处是否唯一，并记录到aim
	int aim = -1;
		for (int i = 1; i <= n; ++i) {
			if (cnt[i] >= 3) {
				if (aim == -1) aim = i;
				else {
					printf("No");
					return 0;
				}
			}
			//顺带记录端点
			if (cnt[i] == 1)end[ne++]=i;
		}

	printf("Yes\n");
	//没有分叉，只有一条路径，直接输出两端
	if (aim == -1) {
		printf("1\n%d %d\n",end[0] ,end[1]);
		return 0;
	}
	//将分叉点看成根节点，每一条边都是从根出发的，拆下来就行了
	printf("%d\n", ne);
	for (int t = 0; t < ne; ++t) {
		printf("%d %d\n", aim, end[t]);
	}
	return 0;
}