【数论】【莫比乌斯反演】【线性筛】bzoj2301 [HAOI2011]Problem b

对于给出的n个询问，每次求有多少个数对(x,y)，满足a≤x≤b，c≤y≤d，且gcd(x,y) = k，gcd(x,y)函数为x和y的最大公约数。

100%的数据满足：1≤n≤50000，1≤a≤b≤50000，1≤c≤d≤50000，1≤k≤50000

看这个：http://blog.csdn.net/a_crazy_czy/article/details/50485082

不过有一点点小错误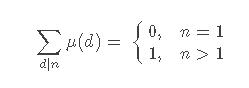，这里0和1反了。

#include<cstdio>
#include<algorithm>
using namespace std;
int n,a,b,c,d,K;
bool notpri[50005];
int pri[50005],mu[50005],sum[50005];
typedef long long ll;
void shai_mu()//线性筛莫比乌斯函数，顺便做出前缀和
{
	notpri[1]=1; mu[1]=1;
	for(int i=2;i<=50000;i++){
		if(!notpri[i]){
			pri[++pri[0]]=i;
			mu[i]=-1;
		}
		for(int j=1;j<=pri[0];j++){
			if((ll)i*(ll)pri[j]>50000ll){
				break;
			}
			notpri[i*pri[j]]=1;
			mu[i*pri[j]]=-mu[i];
			if(i%pri[j]==0){
				mu[i*pri[j]]=0;
				break;
			}
		}
	}
	sum[1]=mu[1];
	for(int i=2;i<=50000;i++){
		sum[i]=sum[i-1]+mu[i];
	}
}
int calc(int n,int m){
	if(n>m){
		swap(n,m);
	}
	int res=0;
	for(int i=1;i<=n/K;){
		int j1=n/(n/(i*K))/K;
		int j2=m/(m/(i*K))/K;
		int j=min(j1,j2);
		res+=(sum[j]-sum[i-1])*(n/(i*K))*(m/(i*K));
		i=j+1;
	}
	return res;
}
int main(){
//	freopen("bzoj2301.in","r",stdin);
	shai_mu();
	scanf("%d",&n);
	for(;n;--n){
		scanf("%d%d%d%d%d",&a,&b,&c,&d,&K);
		printf("%d\n",calc(b,d)-calc(b,c-1)-calc(a-1,d)+calc(a-1,c-1));
	}
	return 0;
}