Django【设计】settings方案

 

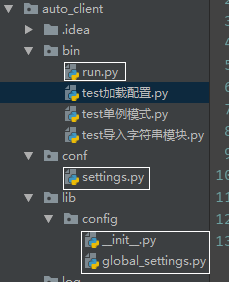
配置文件：

目标：配置文件，默认配置和手动配置分开，参考django的配置文件方案，默认配置文件放在内部，只让用户做常用配置

 

/bin/settings.py（手动配置）

PLUGIN_ITEMS = {
    "nic": "src.plugins.nic.Nic",
    "disk": "src.plugins.disk.Disk",
}

API = "http://127.0.0.1:8000/api/server.html"

 

 

/lib/config/global_settings.py（默认配置）

TEST = True

NAME = "LCQ"

 

/lib/config/__init__.py（/lib/config/目录的初始化文件）

import sys,os
import importlib
from . import global_settings

class Settings():
    """
    global_settings,配置获取
    settings.py，配置获取
    """
    def __init__(self):

        for item in dir(global_settings):
            if item.isupper():
                k = item
                v = getattr(global_settings,item)
                setattr(self,k,v)

        setting_path = os.environ.get('AUTO_CLIENT_SETTINGS')
        md_settings = importlib.import_module(setting_path)
        for item in dir(md_settings):
            if item.isupper():
                k=item
                v=getattr(md_settings,item)
                setattr(self,k,v)

settings = Settings()
# 配置文件直接从这个settings对象拿

 

 

/bin/run.py（启动文件，打印配置内容）

import sys
import os
import importlib
import requests

BASEDIR = os.path.dirname(os.path.dirname(os.path.abspath(__file__)))
sys.path.append(BASEDIR)

os.environ['AUTO_CLIENT_SETTINGS']="conf.settings"
from lib.config import settings

print(settings.NAME)
print(settings.TEST)

 

目录结构：

 

注意：引入配置这种方式在软件设计模式里叫单例模式，因为引入两次也相当于一次

1、导入配置，from lib.config import settings ，这里的lib.config是一个文件夹，从文件夹导入settings？？？ 因为：如果导入文件夹的话，默认导入文件夹下面的__init__.py文件，所以import settings就是__init__.py文件里面的settings。

 

2、settings是一个导入配置文件的对象，__init__.py文件有一个获取配置的类，默认配置和手动配置，实例化一个settings对象，这个对象就包含了所有的配置。