Java实现二叉树的先序、中序、后序、层序遍历（递归和非递归）

二叉树是一种非常重要的数据结构，很多其它数据结构都是基于二叉树的基础演变而来的。对于二叉树，有前序、中序以及后序三种遍历方法。因为树的定义本身就是递归定义，因此采用递归的方法去实现树的三种遍历不仅容易理解而且代码很简洁。而对于树的遍历若采用非递归的方法，就要采用栈去模拟实现。在三种遍历中，前序和中序遍历的非递归算法都很容易实现，非递归后序遍历实现起来相对来说要难一点。

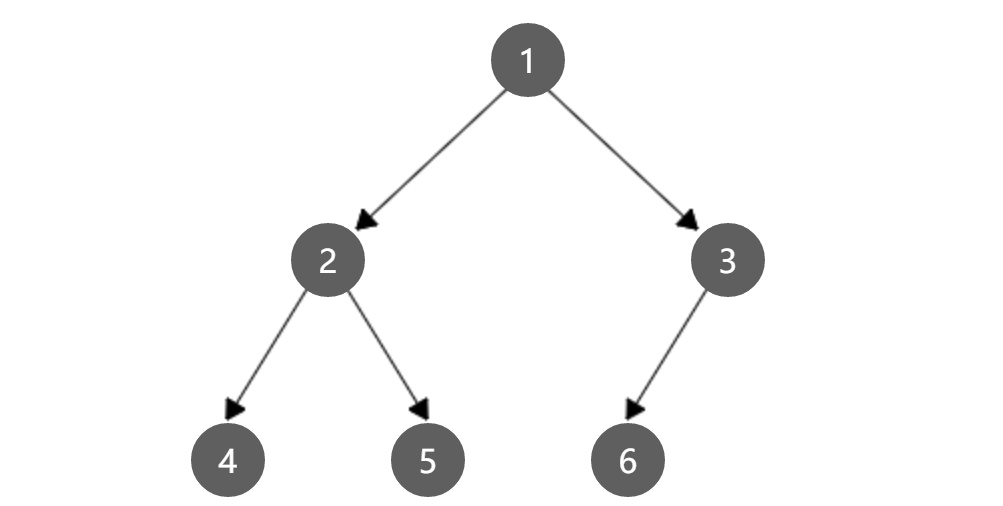
节点分布如下:

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

/**
 * @author 李文浩
 * @version 2017/7/30.
 */
public class BinaryTree {
    /**
     * 节点定义
     */
    static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode(int x) {
            val = x;
        }
    }
    /**
     * 高度，左右子树中的较大值
     *
     * @param node
     * @return
     */
    public static int height(TreeNode node) {
        if (node == null) {
            return 0;
        }
        int leftHeight = height(node.left);
        int rightHeight = height(node.right);
        return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
    }

    /**
     * 层序遍历一颗二叉树，用广度优先搜索的思想，使用一个队列来按照层的顺序存放节点
     * 先将根节点入队列，只要队列不为空，然后出队列，并访问，接着讲访问节点的左右子树依次入队列
     *
     * @param node
     */
    public static void levelTraversal(TreeNode node) {
        if (node == null)
            return;
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(node);
        TreeNode treeNode;
        while (!queue.isEmpty()) {
            treeNode = queue.poll();
            System.out.print(treeNode.val + " ");
            if (treeNode.left != null) {
                queue.offer(treeNode.left);
            }
            if (treeNode.right != null) {
                queue.offer(treeNode.right);
            }
        }
    }

    /**
     * 先序递归
     *
     * @param treeNode
     */
    public static void preOrder(TreeNode treeNode) {
        if (treeNode != null) {
            System.out.print(treeNode.val + " ");
            preOrder(treeNode.left);
            preOrder(treeNode.right);
        }
    }

    /**
     * 中序递归
     *
     * @param treeNode
     */
    public static void inOrder(TreeNode treeNode) {
        if (treeNode != null) {
            inOrder(treeNode.left);
            System.out.print(treeNode.val + " ");
            inOrder(treeNode.right);
        }
    }

    /**
     * 后序递归
     *
     * @param treeNode
     */
    public static void postOrder(TreeNode treeNode) {
        if (treeNode != null) {
            postOrder(treeNode.left);
            postOrder(treeNode.right);
            System.out.print(treeNode.val + " ");
        }
    }

    /**
     * 先序非递归：
     * 这种实现类似于图的深度优先遍历（DFS）。
     * 维护一个栈，将根节点入栈，然后只要栈不为空，出栈并访问，
     * 接着依次将访问节点的右节点、左节点入栈。
     * 这种方式应该是对先序遍历的一种特殊实现（看上去简单明了），
     * 但是不具备很好的扩展性，在中序和后序方式中不适用
     *
     * @param root
     */
    public static void preOrderStack(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode treeNode = stack.pop();
            System.out.print(treeNode.val + " ");
            if (treeNode.right != null) {
                stack.push(treeNode.right);
            }
            if (treeNode.left != null) {
                stack.push(treeNode.left);
            }
        }
    }

    /**
     * 先序非递归2：
     * 利用栈模拟递归过程实现循环先序遍历二叉树。
     * 这种方式具备扩展性，它模拟递归的过程，将左子树点不断的压入栈，直到null，
     * 然后处理栈顶节点的右子树。
     *
     * @param root
     */
    public static void preOrderStack2(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode treeNode = root;
        while (treeNode != null || !stack.isEmpty()) {
            //将左子树点不断的压入栈
            while (treeNode != null) {
                //先访问再入栈
                System.out.print(treeNode.val + " ");
                stack.push(treeNode);
                treeNode = treeNode.left;
            }
            //出栈并处理右子树
            if (!stack.isEmpty()) {
                treeNode = stack.pop();
                treeNode = treeNode.right;
            }

        }

    }

    /**
     * 中序非递归：
     * 利用栈模拟递归过程实现循环中序遍历二叉树。
     * 思想和上面的先序非递归2相同，
     * 只是访问的时间是在左子树都处理完直到null的时候出栈并访问。
     *
     * @param treeNode
     */
    public static void inOrderStack(TreeNode treeNode) {
        Stack<TreeNode> stack = new Stack<>();
        while (treeNode != null || !stack.isEmpty()) {
            while (treeNode != null) {
                stack.push(treeNode);
                treeNode = treeNode.left;
            }
            //左子树进栈完毕
            if (!stack.isEmpty()) {
                treeNode = stack.pop();
                System.out.print(treeNode.val + " ");
                treeNode = treeNode.right;
            }
        }
    }

    public static class TagNode {
        TreeNode treeNode;
        boolean isFirst;
    }

    /**
     * 后序非递归：
     * 后序遍历不同于先序和中序，它是要先处理完左右子树，
     * 然后再处理根(回溯)。
     * <p>
     * <p>
     * 对于任一结点P，将其入栈，然后沿其左子树一直往下搜索，直到搜索到没有左孩子的结点，
     * 此时该结点出现在栈顶，但是此时不能将其出栈并访问，因此其右孩子还为被访问。
     * 所以接下来按照相同的规则对其右子树进行相同的处理，当访问完其右孩子时，该结点又出现在栈顶，
     * 此时可以将其出栈并访问。这样就保证了正确的访问顺序。
     * 可以看出，在这个过程中，每个结点都两次出现在栈顶，只有在第二次出现在栈顶时，才能访问它。
     * 因此需要多设置一个变量标识该结点是否是第一次出现在栈顶，这里是在树结构里面加一个标记，然后合成一个新的TagNode。
     *
     * @param treeNode
     */
    public static void postOrderStack(TreeNode treeNode) {
        Stack<TagNode> stack = new Stack<>();
        TagNode tagNode;
        while (treeNode != null || !stack.isEmpty()) {
            //沿左子树一直往下搜索，直至出现没有左子树的结点
            while (treeNode != null) {
                tagNode = new TagNode();
                tagNode.treeNode = treeNode;
                tagNode.isFirst = true;
                stack.push(tagNode);
                treeNode = treeNode.left;
            }

            if (!stack.isEmpty()) {
                tagNode = stack.pop();
                //表示是第一次出现在栈顶
                if (tagNode.isFirst == true) {
                    tagNode.isFirst = false;
                    stack.push(tagNode);
                    treeNode = tagNode.treeNode.right;
                } else {
                    //第二次出现在栈顶
                    System.out.print(tagNode.treeNode.val + " ");
                    treeNode = null;
                }
            }
        }
    }

    /**
     * 后序非递归2：
     * 要保证根结点在左孩子和右孩子访问之后才能访问，因此对于任一结点P，先将其入栈。如果P不存在左孩子和右孩子，则可以直接访问它；
     * 或者P存在左孩子或者右孩子，但是其左孩子和右孩子都已被访问过了，则同样可以直接访问该结点。
     * 若非上述两种情况，则将P的右孩子和左孩子依次入栈，这样就保证了每次取栈顶元素的时候，左孩子在右孩子前面被访问，
     * 左孩子和右孩子都在根结点前面被访问。
     *
     * @param treeNode
     */
    public static void postOrderStack2(TreeNode treeNode) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode currentTreeNode;
        TreeNode preTreeNode = null;
        stack.push(treeNode);

        while (!stack.isEmpty()) {
            currentTreeNode = stack.peek();
            //如果当前结点没有孩子结点或者孩子节点都已被访问过
            if ((currentTreeNode.left == null && currentTreeNode.right == null) ||
                    (preTreeNode != null && (preTreeNode == currentTreeNode.left || preTreeNode == currentTreeNode.right))) {
                System.out.print(currentTreeNode.val + " ");
                stack.pop();
                preTreeNode = currentTreeNode;
            } else {
                if (currentTreeNode.right != null) {
                    stack.push(currentTreeNode.right);
                }
                if (currentTreeNode.left != null) {
                    stack.push(currentTreeNode.left);
                }
            }
        }
    }
}

参考文档

1. 二叉树的非递归遍历
2. JAVA下实现二叉树的先序、中序、后序、层序遍历（递归和循环）