学习笔记 - 中国剩余定理&扩展中国剩余定理

中国剩余定理&扩展中国剩余定理

NOIP考完回机房填坑

---

◌ 中国剩余定理

处理一类相较扩展中国剩余定理更特殊的问题：

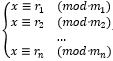
在这里要求 对于任意i,j(i≠j)，gcd(m_i,m_j)=1 （就是互素）

不互素的话就只能用扩展算法了……这也是中国剩余定理与其扩展算法的主要区别。

另外 中国剩余定理 和 扩展中国剩余定理 似乎没有什么关系，除了解决的问题比较相似，所以我就分开讲了。

▫算法

举一个比较常用的例子（出自《九章算术》），求正整数x满足：

先计算 3,5,7 的最小公倍数为 105

再计算出所谓的基础数：

mod 3: 105/3=35 >> 35 mod 3 = 2 （因为35模3本来就余2，就不需要操作） >> 基础数是35

mod 5: 105/5=21 >> 21 mod 5 = 1 （1*3=3，所以需要乘3）>> 21*3 mod 5 = 3 >> 基础数为 21*3=63

mod 7: 105/7=15 >> 15 mod 7 = 1 （1*2=2，所以需要乘2）>> 15*2 mod 7 = 2 >> 基础数为 15*2=30

这3个基础数加起来得到 sum=35+63+30=128

然后模 3,5,7 的最小公倍数就得到答案 ans=128 mod 105=23

▫证明

（背的结论……记不住具体证法，简单证明一下正确性）

可以知道的是：对于带余除法 "a / b = c ... d"，存在 "(ax) / b = (cx+dx/b) ... (dx mod b)"，自己可以举几个例子感性理解一下。

对于集合（元素都互质）A={ a₁,a₂...a_n } 的最小公倍数lcm，lcm/a_i 一定是A中除a_i以外的元素的倍数。如果 lcm/a_i mod a_i = k_i ，而且题目是 求出的数mod a_i = r_i ，如果问题有解，那么一定存在整数 p ，使得(k_i * p) mod a_i = r_i 要使余数乘p，根据前面的思路，我们可以将被除数也乘上 p 。这样被除数就变成了 (lcm/a_i*p) ，它一定被 集合A 中除 a_i 的所有元素整除，并且它模a_i的余数为r_i。这时候我们称这个被除数为a_i的“基础数”

另外一个性质：如果 x₁,x₂,...,x_n 被 a 整除，而 x_n+1 mod a = k ，那么 (x₁+x₂+...+x_n+1) mod a = k。

那么我们现在将 a₁~a_n 的基础数都加起来得到 sum，一定满足 sum mod a_i = r_i ，即已经符合题目要求。但是如果我们要求最小的数，我们可以取模 lcm ，因为 lcm mod ai = 0，所有模一个lcm不会影响到题目要求。

---

◌ 扩展中国剩余定理

解决的问题很相似，只是没有互质的要求。但是依据的算法就完全不一样了。

▫ 证明

个人觉得比中国剩余定理好理解，但是建议先弄懂扩展欧几里得

先只考虑2个元素，即求x：

得到一个奇怪的等式——

　　

再转换一下：

　　

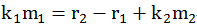
令 

等式两边同时除以 gcd，得到 ：

　　

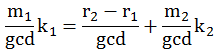
然后将它转换为模运算的形式：

　　

然后因为模运算不能作除法，我们定义：

　　

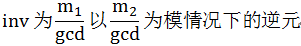
接下来就可以转换模运算了：

　　

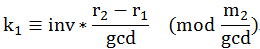
再转回普通运算：

　　

根据一开始的：

　　 

可以得到：

　　

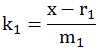
代回去，再移下项：

　　

　　

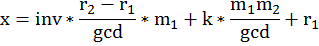
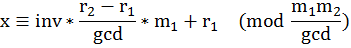
化简一下式子：

　　

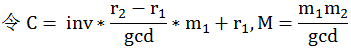
所以就会发现：

　　

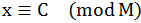
OK……证毕！

---

The End

Thanks for reading!