基于FPGA的DDS设计（二）

　　在DDS设计中，如果相位累加器每个时钟周期累加1，就会输出频率为195.313KHz的波形。如果每个时钟周期累加2，就会输出频率为2*195.313KHz的波形·······，如果每两个时钟周期累加1，就会输出195.313/2KHz的波形······，如果按照这样来设计话，不太方便并且输出波形的频率是不连续的，只能输出一些特殊的频率。

　　首先我们可以一起考虑一个问题，如果我们想要得到一个累加数字0~9，但是想要每次累加的数字有可能是整数也有可能是小数，那么此时整个计算又不让出现小数，应该怎么做呢？我们可以做一个三位数，然后把百位当作我们的输出，然后每次累加的数字自己可以随意调整，也就是相当于之前可以累加小数，小数最小精度为两位小数。000+011=011，123+001=124。如果按照此中方式，让数字一直不断的累加，数字会从最小到最大，不断循环。但是最高位依然是0~9的变化，只不过0~9变化的周期是受到每次累加的值的影响。如果每次累加001，那么百位0~9的循环就需要1000个累加（不要仅仅想0~900，要不断循环），如果每次累加010，那么百位0~9的循环就需要100个累加。

　　如果考虑明白上述的问题，那么在DDS中，我们做了一个相位累加器，但是累加器只是负责ROM地址的输出也就是8位的。如果按照上述思想我们可以设计一个位宽为32位的计数器，把计数器的高八位当作ROM的地址。让计数器每个时钟周期累加1，地址从0增长到255，也就是8‘b00000000~8’b11111111，需要整个32位从全0到全1，一共需要2的32次幂个时钟周期，而这个也就是输出整个波形用的时间----波形周期。我们可以算出周期：2的32次幂*20ns，频率为0.01164153218Hz（这个数字太长了，用f0代替）。每次加1，频率为f0，如果每次加2，频率为2倍的f0。那么我们可以任意整数倍的f0，如果f0足够小（此时f0已经足够小），我们认为可以得到任意频率。如果f0的频率不够小，可以通过增加计数器的位宽来实现。

　　建议读者不要每次加1去仿真，仿真时间太长，并且有可能导致整个仿真器卡主。笔者在此仿真每次累加100K。

 module addr_ctrl (

     input    wire                clk_50m,
     input    wire                rst_n,

     output    wire    [:]        addr
 );

     reg                [:]        cnt;

     assign     addr = cnt[:];

     always @ (posedge clk_50m, negedge rst_n) begin
         if (rst_n == )
             cnt <= ;
         else
             cnt <= cnt + 100_000;
     end

 endmodule 

仿真结果如图8。

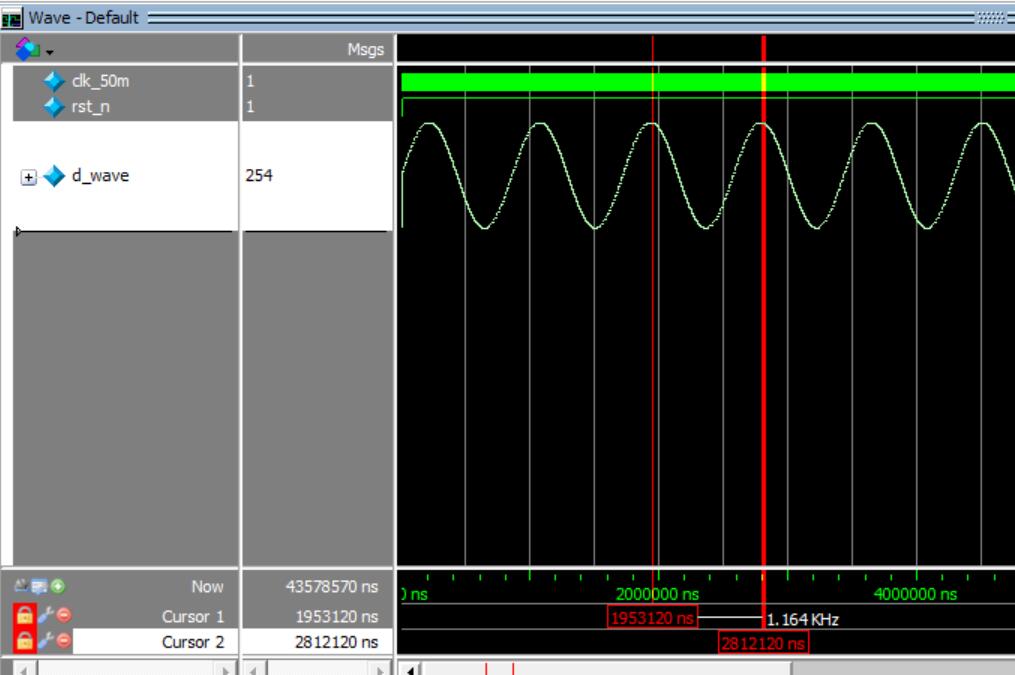
图8

　　每次累加100K，仿真测试频率为1.164KHz。每次累加1，得出的频率为0.01164153218Hz。正好扩大了100K倍。现在我们只要知道做每次累加多少，就能够通过算基础这个频率的多少倍就能算出来频率，但是这么算是会有误差，因为上述得到的频率就是一个近似值。我们可以按照公式去计算频率，假如每次增加N，那么输出波形的周期应该是2的32次幂除以N乘以时钟周期（20ns），用1s除以周期就可以得到频率（如图9）。

图9

　　通过上面的方法，我们可以轻易知道，累加N所对应的频率。但是在实际应用中，往往是想要某一个频率的波形，而不是有了波形算波形的频率是多少。根据外部要求频率，算出来每次累加N的具体数值，这就是频率控制器。其实也是比较简单的，我们把上述公式转换以下就可以了（如图10）。

图10

　　把图10当中的公式在FPGA实现，输入F得到N就是频率控制器。在计算中会有可能存在一些误差，因为有可能计算的数值为12345.24，但是在累加时，会按照12345来进行累加，.24会被忽略，往往会带来一个误差，但是此误差一般都是可以接受的。

　　好了DDS的设计到此结束了，但是如果想要真正输出一个模拟的波形还要驱动一个DAC器件，来达到真正的模拟波形的输出。

　　笔者水平有限，如果设计中，有什么不妥的地方，恳请大佬们指出来。

　　欢迎加好友探讨QQ：746833924，QQ群：173560979。