【题解】前k大子段和

题目描述

Peter喜欢玩数组。NOIP这天，他从Jason手里得到了一个大小为\(n\)的数组。

Peter求出了这个数组的所有子段和，并将这\(\frac{n(n+1)}{2}\)个数降序排列，他想知道前\(k\)个数是什么。

输入输出格式

输入格式

输入数据的第一行包含两个整数\(n\)和\(k\)。

接下来一行包含\(n\)个整数，代表数组。

输出格式

输出\(k\)个数，代表降序之后的前\(k\)个数，用空格隔开。

数据范围

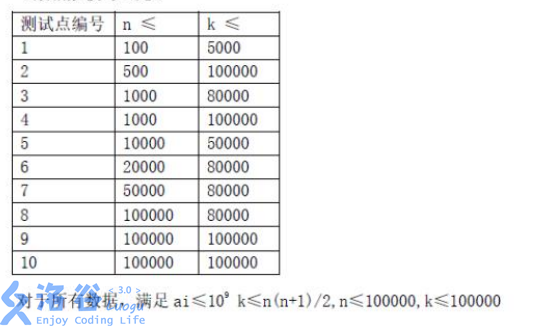
题解

这个题目说的是十分的简洁明了，要求我们求出所有的子段和中前\(k\)大，首先看到这道题的时候，我用的二分答案加树状数组维护虽然在这道题上这种方法会T飞，但是，这种方法是一种方法是一种十分有效的算法。我们先二分答案来枚举第\(k\)大的子段和， 然后再用树状数组来维护和查询（就有点像求逆序对）。

具体过程：

我们每次枚举时，出第\(k\)大子段和为\(x\),那么\(x\)一定可以被表示为\(x = sum[i] - sum[j - 1]\)(\(sum[i]\)表示前缀和)，我们把这个式子移项，可以得到\(sum[j - 1] = sum[i] - x\),这个式子表示当我们遍历到第 \(i\)个前缀和时，已知第\(k\)大的子段和为\(x\)那么我们只用找到\(sum[j - 1]\)之前有多少个\(sum[]\)就可以知道有多少个子段和比\(x\)大了。

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) ((x) & (-x))
const int MAX = 100005;
int n, k;
long long a[MAX], sum[MAX], tree[MAX];
vector <long long> s;

void Add(int x, long long val)
    {
        for(; x <= n; x += lowbit(x))	tree[x] += val;
    }

long long Query(int x)
    {
        long long ret = 0;
        for(;x ; x-= lowbit(x))	ret += tree[x];
        return ret;
    }

int check(int mid)
    {
        int ret = 0;
        memset(tree, 0, sizeof(tree));
        for(int i = 1; i <= n; ++ i)
            {
                int x = sum[i] - mid;
                int it = lower_bound(s.begin(), s.end(), x) - s.begin();
                ret += Query(it);
                if(x > 0) ret ++;
                it = lower_bound(s.begin(), s.end(), sum[i]) - s.begin();
                Add(it + 1, 1);
            }
        return ret;
    }

int main()
{
//	freopen("ksum.in", "r", stdin);
//	freopen("ksum.out", "w", stdout);
    scanf("%d%d", &n, &k);
    for(int i = 1; i <= n; ++ i)
        {
            scanf("%d", &a[i]);
            sum[i] = sum[i - 1] + a[i];
            s.push_back(sum[i]);
        }
    sort(s.begin(), s.end());
    for(int t = 1; t <= k; ++ t)
        {
            long long l = 0, r = sum[n], mid, ans = 0;
            for(;l < r;)
                {
                    mid = (l + r) >> 1;
                    if(check(mid) >= t)	l = mid + 1;
                    else r = mid;
                }
            printf("%lld ", l);
        }
    return 0;
}

如果求取的次数比较少的话，这也会是一个优秀的算法，但是，这道题的\(k\)太大，导致要多次重复这个过程所以，我们要考虑其他解法，因为数组中的数都是非负数，所以，我们可以来贪心。

1. 最大的一定是所有数之和。
2. 每次将最大的去头或去尾可以构成备选答案。

所以我们可以用优先队列来维护，但是，对于\([x,y]\)来说，它可能在\([x - 1, y]\)去头时加入，也有可能在\([x,y + 1]\)去尾时加入，这样就会重复，所以，我们需要一种不会重复的枚举方式，我们把所有前缀和入队，然后每次只考虑去头而不考虑去尾（在前缀和入队时已经去过了），这样就不会重复了。

#include<bits/stdc++.h>
using namespace std;

struct Node{
    int l, r;
    long long sum;
    bool friend operator < (const Node & x, const Node & y)
        {
            return x.sum < y.sum;
        }
};

priority_queue <Node> q;
long long a[100005], sum = 0;

Node make_Node(int l, int r, long long sum)
    {
        Node x;
        x.l = l, x.r = r, x.sum = sum;
        return x;
    }

int main()
{
    int n, k;
    scanf("%d%d", &n, &k);
    for(int i = 1; i <= n; ++ i)
        {
            scanf("%d", &a[i]);
            sum += a[i];
            q.push(make_Node(1, i, sum));
        }
    for(int i = 1; i <= k; ++ i)
        {
            Node x;
            x = q.top(); q.pop();
            printf("%lld ", x.sum);
            q.push(make_Node(x.l + 1, x.r, x.sum - a[x.l]));
        }
    printf("\n");
    return 0;
}