【BZOJ3197】[SDOI2013]刺客信条

【BZOJ3197】[SDOI2013]刺客信条

题面

bzoj

洛谷

题解

关于树的同构，有一个非常好的性质：

把树的重心抠出来，那么会出现两种情况：

1.有一个重心，那么我们直接把这个重心作为树的根。

2.有多个重心，这些重心一定有一条边相连，设重心为\(u,v\),那么把\(u,v\)断开，用一个新的点把

\(u,v\)连起来，将这个点作为根。

最终同构当且仅当与左右两子树分别同构。

有了这条性质，我们继续往下考虑：

设\(f[x][y]\)表示\(x\)的子树与\(y\)的子树同构的最小代价，

怎么转移？

可以分别用\(x,y\)儿子匹配中间的代价来做，

因为他们的儿子肯定是个完美匹配

直接用\(KM\)或费用流进行二分图最大权匹配即可。

对于判断两子树是否相同树哈希即可。

代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
inline int gi() {
	register int data = 0, w = 1;
	register char ch = 0;
	while (!isdigit(ch) && ch != '-') ch = getchar();
	if (ch == '-') w = -1, ch = getchar();
	while (isdigit(ch)) data = 10 * data + ch - '0', ch = getchar();
	return w * data;
}
typedef unsigned long long ull;
const int MAX_N = 1405;
namespace Sol {
	const int INF = 1e9;
	struct Graph {
		int to, next, cap, cost, rev;
	} e[MAX_N << 4];
	int fir[MAX_N], e_cnt, S, T;
	void clearGraph() { fill(&fir[S], &fir[T + 1], -1); e_cnt = 0; }
	void Add_Edge(int u, int v, int cap, int cost) {
		e[e_cnt] = (Graph){v, fir[u], cap, cost, e_cnt + 1};
		fir[u] = e_cnt++;
		e[e_cnt] = (Graph){u, fir[v], 0, -cost, e_cnt - 1};
		fir[v] = e_cnt++;
	}
	int dis[MAX_N], preve[MAX_N], prevv[MAX_N];
	bool inq[MAX_N];
	int min_cost_flow(int s, int t) {
		static queue<int> que; int cost = 0;
		while (1) {
			fill(&dis[s], &dis[t + 1], INF);
			fill(&inq[s], &inq[t + 1], 0);
			inq[s] = 1, dis[s] = 0, que.push(s);
			while (!que.empty()) {
				int x = que.front(); que.pop();
				for (int i = fir[x]; ~i; i = e[i].next) {
					int v = e[i].to;
					if (dis[x] + e[i].cost < dis[v] && e[i].cap > 0) {
						dis[v] = dis[x] + e[i].cost;
						preve[v] = i, prevv[v] = x;
						if (!inq[v]) que.push(v), inq[v] = 1;
					}
				}
				inq[x] = 0;
			}
			if (dis[t] == INF) return cost;
			int d = INF;
			for (int x = t; x != s; x = prevv[x]) d = min(e[preve[x]].cap, d);
			cost += dis[t] * d;
			for (int x = t; x != s; x = prevv[x]) {
				e[preve[x]].cap -= d;
				e[e[preve[x]].rev].cap += d;
			}
		}
	}
}
struct Graph { int to, next; } e[MAX_N << 1]; int fir[MAX_N], e_cnt = 0;
void clearGraph() { memset(fir, -1, sizeof(fir)); e_cnt = 0; }
void Add_Edge(int u, int v) { e[e_cnt] = (Graph){v, fir[u]}; fir[u] = e_cnt++; }
int N, a[MAX_N], b[MAX_N], F[MAX_N], size[MAX_N], Rt;
void getRoot(int x, int fa) {
	size[x] = 1, F[x] = 0;
	for (int i = fir[x]; ~i; i = e[i].next) {
		int v = e[i].to; if (v == fa) continue;
		getRoot(v, x); size[x] += size[v];
		F[x] = max(F[x], size[v]);
	}
	F[x] = max(F[x], N - size[x]);
	if (F[x] < F[Rt]) Rt = x;
}
vector<int> vec1[MAX_N], vec2[MAX_N];
ull hs[MAX_N]; int f[MAX_N][MAX_N], c[MAX_N][MAX_N];
bool cmp(const int &i, const int &j) { return hs[i] < hs[j]; }
void dfs(int x, int fa, vector<int> *vec) {
	size[x] = 1, hs[x] = 0, vec[x].clear();
	for (int i = fir[x]; ~i; i = e[i].next) {
		int v = e[i].to; if (v == fa) continue;
		dfs(v, x, vec); size[x] += size[v], vec[x].push_back(v);
	}
	sort(vec[x].begin(), vec[x].end(), cmp);
	for (int i = vec[x].size() - 1; ~i; --i) hs[x] = hs[x] * N + hs[vec[x][i]];
	hs[x] = hs[x] * N + size[x];
}
int solve(int n) {
	Sol::S = 0, Sol::T = n << 1 | 1;
	Sol::clearGraph();
	for (int i = 1; i <= n; i++) {
		Sol::Add_Edge(Sol::S, i, 1, 0), Sol::Add_Edge(i + n, Sol::T, 1, 0);
		for (int j = 1; j <= n; j++) Sol::Add_Edge(i, j + n, 1, c[i][j]);
	}
	return Sol::min_cost_flow(Sol::S, Sol::T);
}
int Dp(int x, int y) {
	if (f[x][y] != -1) return f[x][y];
	f[x][y] = a[x] ^ b[y];
	for (int i = 0, j, sz = vec1[x].size() - 1; i <= sz; i++) {
		j = i; while (j < sz && hs[vec1[x][j + 1]] == hs[vec1[x][i]]) ++j;
		for (int k = i; k <= j; k++)
			for (int l = i; l <= j; l++)
				Dp(vec1[x][k], vec2[y][l]);
		for (int k = i; k <= j; k++)
			for (int l = i; l <= j; l++)
				c[k - i + 1][l - i + 1] = Dp(vec1[x][k], vec2[y][l]);
		f[x][y] += solve(j - i + 1); i = j;
	}
	return f[x][y];
}
int main () {
	clearGraph();
	N = gi(), F[0] = N;
	for (int i = 1; i < N; i++) {
		int u = gi(), v = gi();
		Add_Edge(u, v), Add_Edge(v, u);
	}
	for (int i = 1; i <= N; i++) a[i] = gi();
	for (int i = 1; i <= N; i++) b[i] = gi();
	getRoot(1, 0); dfs(Rt, 0, vec2); ull res = hs[Rt];
	int ans = N;
	for (int i = 1; i <= N; i++) {
		dfs(i, 0, vec1);
		if (hs[i] == res) {
			memset(f, -1, sizeof(f));
			ans = min(ans, Dp(i, Rt));
		}
	}
	printf("%d\n", ans);
	return 0;
}

一些题外话

\(KM\)与费用流的速度对比(不开O2)：

我的费用流：

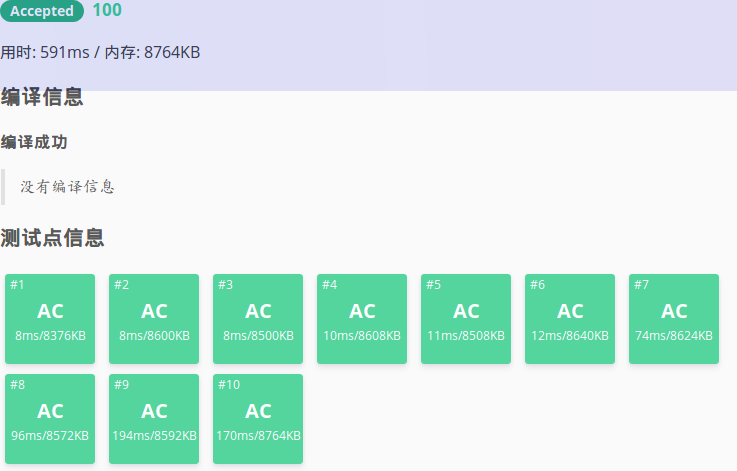
\(xgzc\)的辣鸡\(KM\):

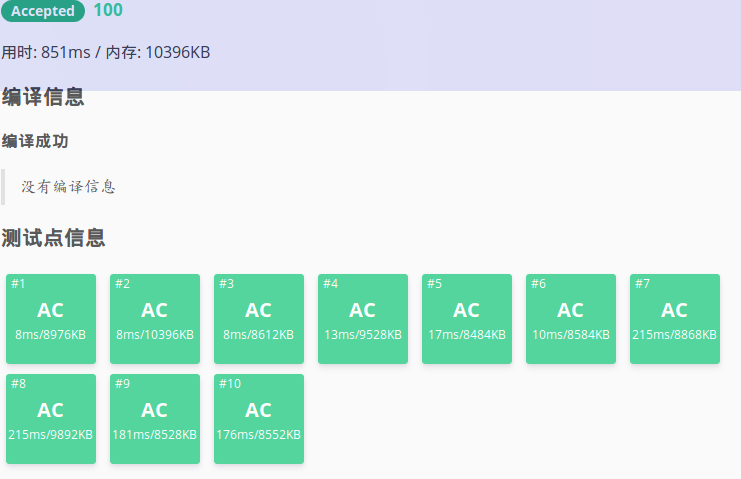
\(zzx\)的豪华版\(KM\):

所以用费用流也不是不行