【RL系列】蒙特卡罗方法——Soap Bubble

“肥皂泡”问题来源于Reinforcement Learning: An Introduction(2017). Exercise 5.2，大致的描述如下：

用一个铁丝首尾相连组成闭合曲线，浸入肥皂泡液，拿起后，可以发现肥皂泡液以这个闭合曲线为边界形成了一个曲面。如何将这个曲面描述出来，便是肥皂泡问题的核心。

若想使得肥皂泡液形成一个稳固的曲面，肥皂泡上的每一个点所受到的合力均为0，所以这意味着该点所处的位置是周边所有点位置的均值（在这里忽略重力的影响，肥皂泡的密度量级与空气相当）。所以在计算曲面时，可以先将闭合曲线投影到x-y平面上，然后用一个点的高度（坐标z）来表示曲面上该点周边所有点位置的均值（该点位置的x，y值是不变的）。

常用的方法是迭代法，依次迭代求解投影到x-y平面上的闭合曲线包围的点的高度值。不过当计算某一个或某几个点的高度时可以使用Monte Carlo Method提高计算效率。

先来尝试一下迭代法求解，这里直接给出算法流程：

1. 投影闭合曲线到x-y平面
2. 从闭合曲线内的第一个点开始迭代
3. 当前被迭代的点在x-y平面上的位置为(x, y)，则高度hight，$ H(x, y) $可用该公式计算：$$ H(x, y) = \frac{1}{4}(H(x + 1, y) + H(x - 1, y) + H(x, y + 1) + H(x, y - 1)) $$
4. 到达闭合曲线内的最后一个点，判断高度$ H $是否收敛，如未收敛继续迭代。

我们用这个闭合曲线作为实验对象：

计算得到的曲面图形如下：

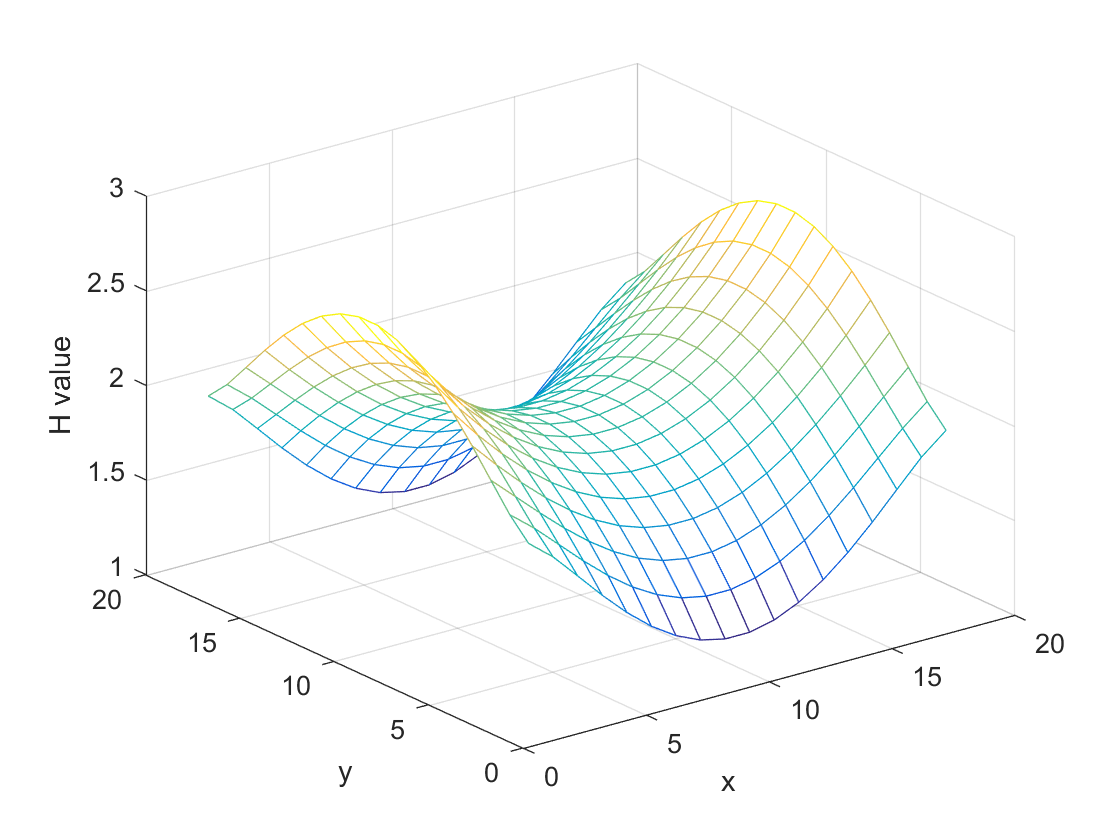
迭代法有一个缺陷在于，如果需要计算某一点的高度，则必须计算曲面上所有点的高度。对于只是计算某一点的情况，这个方法无疑是效率低下的。在这种情况下，Monte Carlo Method提供了一种非常高效的计算方案。这里可以运用Monte Carlo方法前提是，曲面上某个点的高度可以等效为边界所有点的高度相关于与之距离的加权平均。所以使用Monte Carlo的关键在于，以需要计算的那一点为起始点，开始随机游走，碰到边界上某个点的概率与起始点和该点的距离相关，距离近则概率高，距离远则概率低。在随机游走的过程中，将所碰到的边界点的高度取平均数，即为起始点高度的估计。Monte Carlo Method的算法流程如下：

1. 投影闭合曲线到x-y平面
2. 确定起始点(x, y)，开始迭代
3. 随机选择动作开始游走
4. 判断是否碰到边界，如碰到边界，记录边界高度值$ H_b $。未碰到则继续游走。
5. 判断是否收敛，未收敛则回到第三步重新开始。
6. 起始点高度值的估计可以计算为（Num为迭代次数）：$$ H(x, y) = \frac{\sum H_b}{Num} $$

可以比较一下两种方法的高度值收敛曲线，以坐标(10, 10)为例：

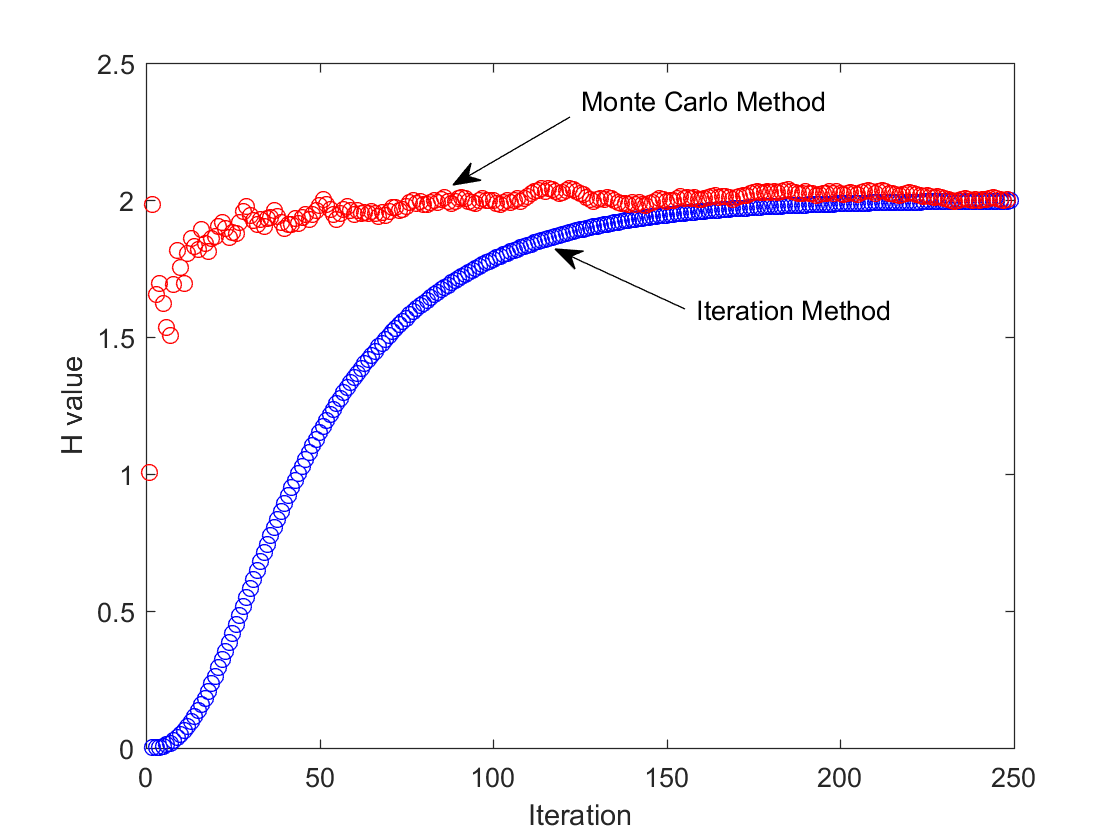
可以发现在计算坐标(10, 10)的高度值时，Monte Carlo Method的收敛速度比Iteration Method快很多，但准确度却要差一些。