树形结构的数据库表Schema设计-基于左右值编码

树形结构的数据库表Schema设计

程序设计过程中，我们常常用树形结构来表征某些数据的关联关系，如企业上下级部门、栏目结构、商品分类等等，通常而言，这些树状结构需要借助于数据库完
成持久化。然而目前的各种基于关系的数据库，都是以二维表的形式记录存储数据信息，因此是不能直接将Tree存入DBMS，设计合适的Schema及其对
应的CRUD算法是实现关系型数据库中存储树形结构的关键。

理想中树形结构应该具备如下特征：数据存储冗余度小、直观性强；检索遍历过程简单高效；节点增删改查CRUD操作高效。无意中在网上搜索到一种很巧妙的
设计，原文是英文，看过后感觉有点意思，于是便整理了一下。本文将介绍两种树形结构的Schema设计方案：一种是直观而简单的设计思路，另一种是基于左
右值编码的改进方案。

一、基本数据

本文列举了一个食品族谱的例子进行讲解，通过类别、颜色和品种组织食品，树形结构图如下：

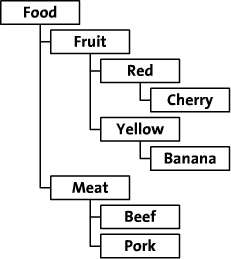
二、继承关系驱动的Schema设计

对树形结构最直观的分析莫过于节点之间的继承关系上，通过显示地描述某一节点的父节点，从而能够建立二维的关系表，则这种方案的Tree表结构通常设计为：{Node_id,Parent_id}，上述数据可以描述为如下图所示：

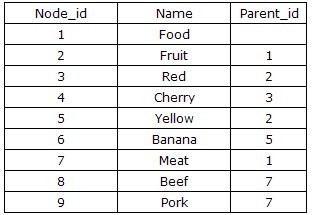
这种方案的优点很明显：设计和实现自然而然，非常直观和方便。缺点当然也是非常的突出：由于直接地记录了节点之间的继承关系，因此对Tree的任何
CRUD操作都将是低效的，这主要归根于频繁的“递归”操作，递归过程不断地访问数据库，每次数据库IO都会有时间开销。当然，这种方案并非没有用武之
地，在Tree规模相对较小的情况下，我们可以借助于缓存机制来做优化，将Tree的信息载入内存进行处理，避免直接对数据库IO操作的性能开销。

三、基于左右值编码的Schema设计

在基于数据库的一般应用中，查询的需求总要大于删除和修改。为了避免对于树形结构查询时的“递归”过程，基于Tree的前序遍历设计一种全新的无递归查询、无限分组的左右值编码方案，来保存该树的数据。

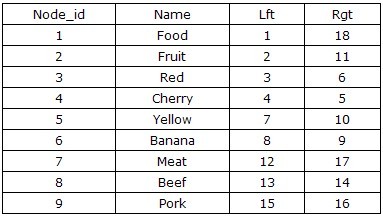
第一次看见这种表结构，相信大部分人都不清楚左值（Lft）和右值（Rgt）是如何计算出来的，而且这种表设计似乎并没有保存父子节点的继承关系。但当
你用手指指着表中的数字从1数到18，你应该会发现点什么吧。对，你手指移动的顺序就是对这棵树进行前序遍历的顺序，如下图所示。当我们从根节点Food
左侧开始，标记为1，并沿前序遍历的方向，依次在遍历的路径上标注数字，最后我们回到了根节点Food，并在右边写上了18。

第一次看见这种表结构，相信大部分人都不清楚左值（Lft）和右值（Rgt）是如何计算出来的，而且这种表设计似乎并没有保存父子节点的继承关系。但当
你用手指指着表中的数字从1数到18，你应该会发现点什么吧。对，你手指移动的顺序就是对这棵树进行前序遍历的顺序，如下图所示。当我们从根节点Food
左侧开始，标记为1，并沿前序遍历的方向，依次在遍历的路径上标注数字，最后我们回到了根节点Food，并在右边写上了18。

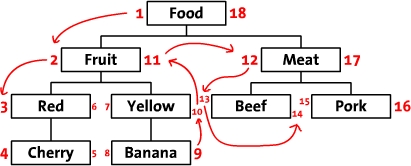
依据此设计，我们可以推断出所有左值大于2，并且右值小于11的节点都是Fruit的后续节点，整棵树的结构通过左值和右值存储了下来。然而，这还不够，我们的目的是能够对树进行CRUD操作，即需要构造出与之配套的相关算法。

四、树形结构CRUD算法

（1）获取某节点的子孙节点

只需要一条SQL语句，即可返回该节点子孙节点的前序遍历列表，以Fruit为例：SELECT* FROM Tree WHERE Lft BETWEEN 2 AND 11 ORDER BY Lft ASC。查询结果如下所示：

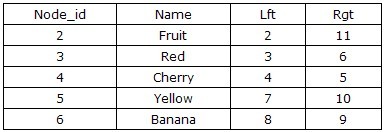
那么某个节点到底有多少的子孙节点呢？通过该节点的左、右值我们可以将其子孙节点圈进来，则子孙总数 = (右值 – 左值– 1) /
2，以Fruit为例，其子孙总数为：(11 –2 – 1) / 2 =
4。同时，为了更为直观地展现树形结构，我们需要知道节点在树中所处的层次，通过左、右值的SQL查询即可实现，以Fruit为
例：SELECTCOUNT(*) FROM Tree WHERE Lft <= 2 AND Rgt
>=11。为了方便描述，我们可以为Tree建立一个视图，添加一个层次数列，该列数值可以写一个自定义函数来计算，函数定义如下：

[sql] view
plaincopy

 

1. CREATEFUNCTION

   int

   RETURNSint
   AS
   begin
   declareint
   set
   declareint
   declareint
   selectfromwhere
   begin
   selectfromwhere
   select(*) fromwhere Rgt >= @rgt

2. end
   return
   end
   GO

基于层次计算函数，我们创建一个视图，添加了新的记录节点层次的数列：

[sql] view
plaincopy

 

1. CREATEVIEW
   AS
   SELECTNameASFROMORDERBY
   GO

创建存储过程，用于计算给定节点的所有子孙节点及相应的层次：

[sql] view
plaincopy

 

1. CREATEPROCEDURE

   int

   AS
   declareint
   declareint
   selectfromwhere
   begin
   selectfromwhere
   selectfromwhere @lft  @rgt orderbyASC
   end
   GO

现在，我们使用上面的存储过程来计算节点Fruit所有子孙节点及对应层次，查询结果如下：

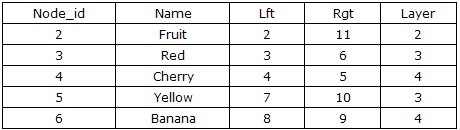
从上面的实现中，我们可以看出采用左右值编码的设计方案，在进行树的查询遍历时，只需要进行2次数据库查询，消除了递归，再加上查询条件都是数字的比
较，查询的效率是极高的，随着树规模的不断扩大，基于左右值编码的设计方案将比传统的递归方案查询效率提高更多。当然，前面我们只给出了一个简单的获取节
点子孙的算法，真正地使用这棵树我们需要实现插入、删除同层平移节点等功能。

（2）获取某节点的族谱路径

假定我们要获得某节点的族谱路径，则根据左、右值分析只需要一条SQL语句即可完成，以Fruit为例：SELECT* FROM Tree
WHERE Lft < 2 AND Rgt > 11 ORDER BY Lft ASC ，相对完整的存储过程：

[sql] view
plaincopy

 

1. CREATEPROCEDURE

   int

   AS
   declareint
   declareint
   selectfromwhere
   begin
   selectfromwhere
   selectfromwhere Rgt > @rgt orderbyASC
   end
   GO

（3）为某节点添加子孙节点

    假定我们要在节点“Red”下添加一个新的子节点“Apple”，该树将变成如下图所示，其中红色节点为新增节点。

仔细观察图中节点左右值变化，相信大家都应该能够推断出如何写SQL脚本了吧。我们可以给出相对完整的插入子节点的存储过程：

[sql] view
plaincopy

 

1. CREATEPROCEDURE

   int
   varchar

   AS
   declareint
   selectfromwhere
   begin
   SETON
   BEGIN
   selectfromwhere
   updatesetwhere
   updatesetwhere
   insertintoNamevalues
   COMMITTRANSACTION
   SETOFF
   end
   GO

（4）删除某节点

如果我们想要删除某个节点，会同时删除该节点的所有子孙节点，而这些被删除的节点的个数为：(被删除节点的右值 – 被删除节点的左值+ 1) /
2，而剩下的节点左、右值在大于被删除节点左、右值的情况下会进行调整。来看看树会发生什么变化，以Beef为例，删除效果如下图所示。

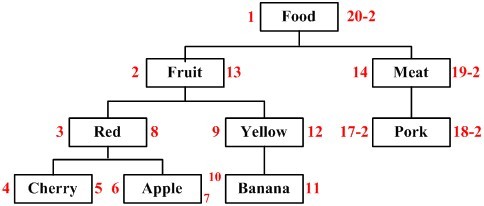
则我们可以构造出相应的存储过程：

[sql] view
plaincopy

 

1. CREATEPROCEDURE

   int

   AS
   declareint
   declareint
   selectfromwhere
   begin
   SETON
   BEGIN
   selectfromwhere
   deletefromwhere Rgt <= @rgt

2. updatesetwhere
   updatesetwhere
   COMMITTRANSACTION
   SETOFF
   end
   GO

五、总结

我们可以对这种通过左右值编码实现无限分组的树形结构Schema设计方案做一个总结：

（1）优点：在消除了递归操作的前提下实现了无限分组，而且查询条件是基于整形数字的比较，效率很高。

（2）缺点：节点的添加、删除及修改代价较大，将会涉及到表中多方面数据的改动。

当然，本文只给出了几种比较常见的CRUD算法的实现，我们同样可以自己添加诸如同层节点平移、节点下移、节点上移等操作。有兴趣的朋友可以自己动手编
码实现一下，这里不在列举了。值得注意的是，实现这些算法可能会比较麻烦，会涉及到很多条update语句的顺序执行，如果顺序调度考虑不周详，出现
Bug的话将会对整个树形结构表产生惊人的破坏。因此，在对树形结构进行大规模修改的时候，可以采用临时表做中介，以降低代码的复杂度，同时，强烈推荐在
做修改之前对表进行完整备份，以备不时之需。在以查询为主的绝大多数基于数据库的应用系统中，该方案相比传统的由父子继承关系构建的数据库Schema更
为适用。

参考文献：《Storing Hierarchical Data in
a Database Article》

转载：http://blog.csdn.net/dreajay/article/details/8894058