python求微分方程组的数值解曲线01

本人最近在写一篇关于神经网络同步的文章，其一部分模型为：

x_i^{\Delta}(t)= -a_i*x_i(t)+ b_i* f(x_i(t))+ \sum\limits_{j \in\{i-1, i+1\}}c_{ij}f(x_j(t-\tau_{ij})), t\in\mathbb{R}　　　　(1.1)

y_i^{\Delta}(t)= -a_i*y_i(t)+ b_i* f(y_i(t))+ \sum\limits_{j \in\{i-1, i+1\}}c_{ij}f(y_j(t-\tau_{ij})), t\in\mathbb{R}　　　　(1.2)

下面利用python求(1.1)-(1.2)的数值解并作出图形：

# Numerical simulation for 3-rd paper
# Author: Qiang Xiao
# Time: 2015-06-22

import matplotlib.pyplot as plt
import numpy as np

a= 0.5
b= -0.5
c= 0.5
tau= 1
k= 2
delta= 0.1
T= 200
row= 6
col= int(T/delta)
N= 6

x= np.zeros((row, col))
dx= np.zeros((row, col))
y= np.zeros((row, col))
dy= np.zeros((row, col))

x0= [5,2,1,0,1,4]
y0= [-5,2,-3,-2,0,-3]
for i in range(N):
    x[i,0:int(tau/delta)+ 1]= x0[i]
    y[i,0:int(tau/delta)+ 1]= y0[i]

print np.e

def f(t):
    return np.cos(t)

def j(i):
    if i== 0:
    　　return 1, 5
    elif i== 5:
    　　return 4, 0
    else:
   　　 return i-1, i+1

for time in range(int(tau/delta),int(T/delta)-1):
    for i in range(6):
    　　dx[i, time]= -a* x[i, time]+ b*f(x[i, time])+ c*f(x[int(j(i)[0]), time- 10])+ c*f(x[int(j(i)[1]), time- 10])
    　　dy[i, time]= -a* y[i, time]+ b*f(y[i, time])+ c*f(y[int(j(i)[0]), time- 10])+ c*f(y[int(j(i)[1]), time- 10])+ k*(x[i, time]- y[i, time])
        x[i, time+1]= x[i, time]+ delta*dx[i, time]
        y[i, time+1]= y[i, time]+ delta*dy[i, time]

tt= np.arange(tau,T,delta)
print len(tt)

plt.plot(tt,x[0,10:int(T/delta)],'c')
plt.plot(tt,y[0,10:int(T/delta)],'c.')
plt.plot(tt,x[1,10:int(T/delta)],'r.')
plt.plot(tt,y[1,10:int(T/delta)],'r')
plt.plot(tt,x[2,10:int(T/delta)],'b')
plt.plot(tt,y[2,10:int(T/delta)],'b.')
plt.plot(tt,x[3,10:int(T/delta)],'k')
plt.plot(tt,y[3,10:int(T/delta)],'k.')
plt.plot(tt,x[4,10:int(T/delta)],'m')
plt.plot(tt,y[4,10:int(T/delta)],'m.')
plt.plot(tt,x[5,10:int(T/delta)],'y')
plt.plot(tt,y[5,10:int(T/delta)],'y.')

plt.xlabel('Time t')
plt.ylabel('xi(t) and yi(t)')
plt.legend(('x1','y1','x2','y2','x3','y3','x4','y4','x5','y5','x6','y6'))
plt.show()

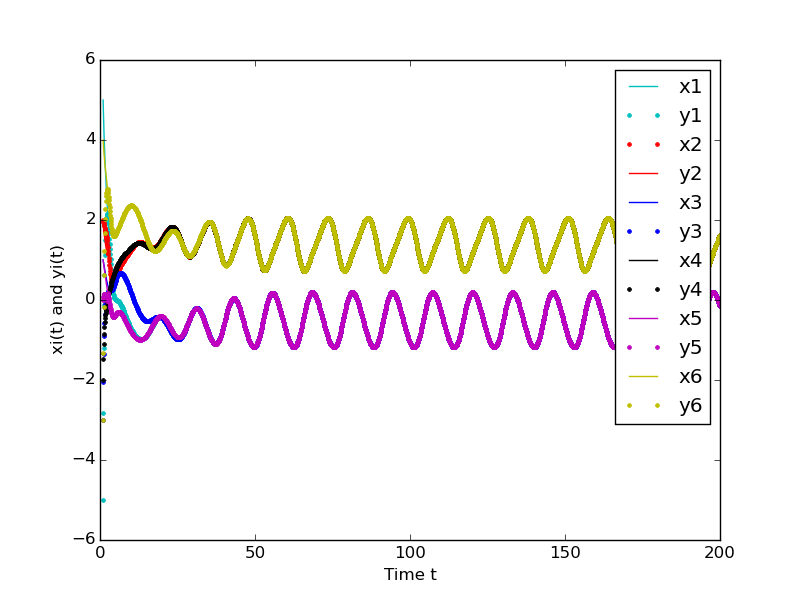
由上图可以看出，网络单元x_i(t) 与 y_i(t) 分别达成了同步。

欢迎交流！