click through rate prediction

包括内容如下图：

使用直接估计法，置信区间置信率的估计：

1.使用二项分布直接估计

$p(0.04<\hat{p}<0.06) = \sum_{0.04n\leq k \leq 0.06n}{n \choose k}0.05^{k}0.95^{n-k}$

low=ceil(n*0.04);%上取整
high=floor(n*0.06);%下取整
prob = 0;
for i=low:1:high
    prob = prob+nchoosek(n,i)*(0.05^i)*(0.95^(n-i));
end

2.使用正态分布近似

$\mu = p = 0.05,\sigma^2 = \frac{p(1-p)}{n} = \frac{0.05*0.95}{n}$

normcdf(0.06,0.05,sigma/x(i)^0.5) - normcdf(0.04,0.05,sigma/x(i)^0.5)

warning off all;
clear all;clc;close all;
x=500:1:1500;
y = zeros(1,size(x,2));
y2 = zeros(1,size(x,2));
sigma = sqrt(0.05*0.95);
for i =1:size(x,2)
    y(i) = adPredict(x(i));
    y2(i) = normcdf(0.06,0.05,sigma/x(i)^0.5) - normcdf(0.04,0.05,sigma/x(i)^0.5);
end
 
plot(x,y,'b-'); hold on;
plot(x,y2,'r-');
hold on;
x1=[500 1500];
y1=[0.85 0.85];
plot(x1,y1,'y-');

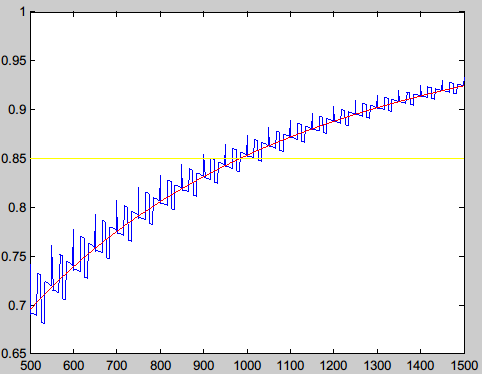
打印曲线：观测到，n=1000，差不多置信度会到达0.85

AUC概念及计算：

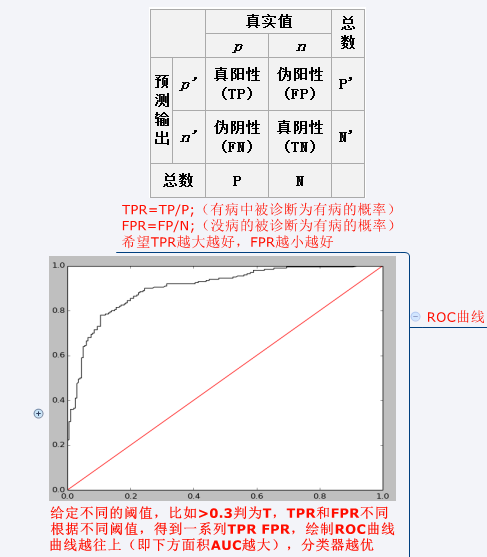
sklearn代码：sklearn中有现成方法，计算一组TPR,FPR，然后plot就可以；AUC也可以直接调用方法。

import numpy as np
import matplotlib.pyplot as plt
 
from sklearn.linear_model import LogisticRegression
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import roc_auc_score
from sklearn.metrics import roc_curve
 
digits = datasets.load_digits()
 
X, y = digits.data, digits.target
X = StandardScaler().fit_transform(X)
 
# classify small against large digits
y = (y > 4).astype(np.int)
X_train = X[:-400]
y_train = y[:-400]
 
X_test = X[-400:]
y_test = y[-400:]
 
lrg = LogisticRegression(penalty='l1')
lrg.fit(X_train, y_train)
 
y_test_prob=lrg.predict_proba(X_test)
P = np.where(y_test==1)[0].shape[0];
N  = np.where(y_test==0)[0].shape[0];
 
dt = 10001
TPR = np.zeros((dt,1))
FPR = np.zeros((dt,1))
for i in range(dt):
    y_test_p = y_test_prob[:,1]>=i*(1.0/(dt-1))
    TP = np.where((y_test==1)&(y_test_p==True))[0].shape[0];
    FN = P-TP;
    FP = np.where((y_test==0)&(y_test_p==True))[0].shape[0];
    TN = N - FP;
    TPR[i]=TP*1.0/P
    FPR[i]=FP*1.0/N
 
plt.plot(FPR,TPR,color='black')
plt.plot(np.array([[0],[1]]),np.array([[0],[1]]),color='red')
plt.show()
 
#use sklearn method
# fpr, tpr, thresholds = roc_curve(y_test,y_test_prob[:,1],pos_label=1)
# plt.plot(fpr,tpr,color='black')
# plt.plot(np.array([[0],[1]]),np.array([[0],[1]]),color='red')
# plt.show()
 
rank = y_test_prob[:,1].argsort()
rank = rank.argsort()+1
auc = (sum(rank[np.where(y_test==1)[0]])-(P*1.0*(P+1)/2))/(P*N);
print auc
print roc_auc_score(y_test, y_test_prob[:,1])