POJ 1052 Plato's Blocks

 

Plato's Blocks

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 734		Accepted: 296

Description

Plato believed what we perceive is but a shadow of reality. Recent archaeological excavations have uncovered evidence that this belief may have been encouraged by Plato's youthful amusement with cleverly-designed blocks. The blocks have the curious property that, when held with any face toward a light source, they cast shadows of various letters, numbers, shapes, and patterns. It is possible for three faces incident to a corner to correspond to three different shadow patterns. Opposite faces, of course, cast shadows which are mirror images of one another. 
The blocks are formed by gluing together small cubes to form a single, connected object. As an example, the figures below show, layer by layer, the internal structure of a block which can cast shadows of the letters "E", "G", or "B". 

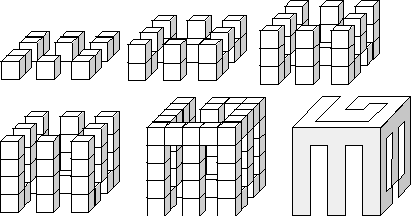
Only a partial set of blocks was discovered, but the curious scientists would like to determine what combinations of shadows are possible. Your program, the solution to this problem, will help them! The program will input groups of shadow patterns, and for each group will report whether or not a solid can be constructed that will cast those three shadows. 

Input

The input contains a sequence of data sets, each specifying a dimension and three shadow patterns. The first line of a data set contains a positive integer 1 <= n <= 20 that specifies the dimensions of the input patterns. The remainder of the data set consists of 3n lines, each containing a string of n "X" and "-" characters. Each group of n lines represents a pattern. Where an "X" appears a shadow should be cast by the final solid, and where a "-" appears, light should pass through. For this problem, the input patterns may be assumed to have at least one "X" along each edge of the pattern. The input is terminated by a line containing a single zero in place of a valid dimension. 

Output

For each data set in the input, output the data set number and one of the following messages:

Valid set of patterns 
Impossible combination 
For a set of patterns to be considered valid, it must be possible to construct, by gluing unit cubes together along their faces, a one-piece solid capable of casting the shadow of each of the input patterns. 

Sample Input

5
XXXXX
X----
X--XX
X---X
XXXXX
XXXXX
X----
XXXXX
X----
XXXXX
XXXXX
X---X
XXXX-
X---X
XXXXX
3
X--
-X-
--X
XX-
XXX
-XX
-XX
XXX
XX-
0

Sample Output

Data set 1: Valid set of patterns
Data set 2: Impossible combination

这个问题刚开始没有思路，看了网上的一些方法，就自己写了一个；

 //注意每个面都由八种方式，旋转+翻转
 //先建一个完整的立方块，然后删去中间的空缺部分
 //最后检查一下（深搜）是不是所有的小立方块都连在一起

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>

 using namespace std;
 char mpr[][];
 int n;
 char mp[][][][];
 char cube[][][];
 int dx[]={,,,,,-};
 int dy[]={,,,-,,};
 int dz[]={,-,,,,};
 void cs(int t)
 {
     for(int i=;i<n;i++)
         for(int j=;j<n;j++)
             mp[t][][i][j]=mpr[i][j];
     for(int i=;i<n;i++)
         for(int j=;j<n;j++)
             mp[t][][i][j]=mp[t][][i][n--j];
     for(int i=;i<n;i++)
         for(int j=;j<n;j++)
             mp[t][][i][j]=mp[t][][j][n--i];
     for(int i=;i<n;i++)
         for(int j=;j<n;j++)
             mp[t][][i][j]=mp[t][][i][n--j];
     for(int i=;i<n;i++)
         for(int j=;j<n;j++)
             mp[t][][i][j]=mp[t][][j][n--i];
     for(int i=;i<n;i++)
         for(int j=;j<n;j++)
             mp[t][][i][j]=mp[t][][i][n--j];
     for(int i=;i<n;i++)
         for(int j=;j<n;j++)
             mp[t][][i][j]=mp[t][][j][n--i];
     for(int i=;i<n;i++)
         for(int j=;j<n;j++)
             mp[t][][i][j]=mp[t][][i][n--j];
 }
 int checkview1(int a)
 {
     for(int i=;i<n;i++)
         for(int j=;j<n;j++)
     {
         if(mp[][a][i][j]=='X')
         {
             int flag=;
             for(int k=;k<n;k++)
                 if(cube[i][j][k]==)
                     flag=;
             if(flag==) return ;
         }
     }
     return ;
 }
 int checkview2(int a)
 {
     for(int i=;i<n;i++)
         for(int j=;j<n;j++)
     {
         if(mp[][a][i][j]=='X')
         {
             int flag=;
             for(int k=;k<n;k++)
                 if(cube[i][k][j]==)
                     flag=;
             if(flag==) return ;
         }
     }
     return ;
 }
 int checkview3(int a)
 {
     for(int i=;i<n;i++)
         for(int j=;j<n;j++)
     {
         if(mp[][a][i][j]=='X')
         {
             int flag=;
             for(int k=;k<n;k++)
                 if(cube[k][i][j]==)
                     flag=;
             if(flag==) return ;
         }
     }
     return ;
 }
 int check(int x,int y,int z)
 {
     if(x<n&&x>=&&y<n&&y>=&&z<n&&z>=) return ;
     return ;
 }
 void dfs(int a,int b,int c)
 {
     for(int i=;i<;i++)
     {
         int curx=a+dx[i];
         int cury=b+dy[i];
         int curz=c+dz[i];
         if(check(curx,cury,curz)&&cube[curx][cury][curz]==)
         {
             cube[curx][cury][curz]=;
             dfs(curx,cury,curz);
         }
     }
     return ;
 }
 int Num()
 {
     int num=;
     for(int i=;i<n;i++)
         for(int j=;j<n;j++)
             for(int k=;k<n;k++)
                 if(cube[i][j][k]==)
         {
             cube[i][j][k]=;
             dfs(i,j,k);
             num++;
         }
     if(num>) return ;
     return ;
 }
 int solve(int a,int b,int c)
 {
     //建一个完全的立方块
     memset(cube,,sizeof(cube));

     //删去其中的空缺部分
     for(int i=;i<n;i++)
         for(int j=;j<n;j++)
             if(mp[][a][i][j]=='-')
                 for(int k=;k<n;k++)
                     cube[i][j][k]=;
     for(int i=;i<n;i++)
         for(int j=;j<n;j++)
             if(mp[][b][i][j]=='-')
                 for(int k=;k<n;k++)
                     cube[i][k][j]=;
     for(int i=;i<n;i++)
         for(int j=;j<n;j++)
             if(mp[][c][i][j]=='-')
                 for(int k=;k<n;k++)
                     cube[k][i][j]=;

     //检查三视图是否还是符合的还有立方块是否都连在一起（dfs）
     if(checkview1(a)&&checkview2(b)&&checkview3(c)&&Num())
         return ;
     return ;
 }
 int main()
 {
     int num=;
     while(cin >> n&&n)
     {
         for(int i=;i<;i++)
         {
             for(int j=;j<n;j++)
                 cin >> mpr[j];
             cs(i);//这里构建八个面，那么8*8*8=512种情况，只要有一种情况符合就行了
         }
         int flag=;
         for(int i=;i<;i++)
             for(int j=;j<;j++)
                 for(int k=;k<;k++)
                     if(solve(i,j,k))//检查每种情况是否符合
                         flag=;
         if(flag)
             printf("Data set %d: Valid set of patterns\n",num++);
         else printf("Data set %d: Impossible combination\n",num++);
     }
     return ;
 }