TSP问题（旅行商问题）[分支限界法]

问题：

　　旅行商从 a 开始周游下图所有的城市一次，然后回到 a，城市之间的旅行代价在图中标明。

　　请选择一个最优的行走顺序使得周游所有城市的代价最小。

　　　　　　

思路：

　　随便怎么周游，对于一个城市来说，一定有一条进的路和一条出的路。

　　对于每个城市来说，暂时都选取代价最小的两条路来作为理想的路线，就算这些路不合理。

　　比如对于 a 来说，选择 a<->c(1) & a<->b(3) ；对于 e 来说，选择 e<->c(2) & e<->d(3)。

　　把所有的这些值加起来除以2，

　　本题即 lb=[(a<->c+a<->b)+(b<->a+b<->c)+(c<->a+c<->e)+(d<->e+d<->c)+(e<->c+e<->d)]/2=[(1+3)+(3+6)+(1+2)+(3+4)+(2+3)]/2=14 .

　　 把这个值当成是理想的最小代价，然后接下来搜索解空间树的时候，都在该基础上进行。

　　下面画出搜索解空间树的过程，其中方框上面的是点的名称，下面是假设的理想周游代价，方框头顶是搜索顺序：

　　刚开始从 a 走

　　

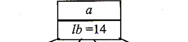
　　从 a 可以到达 b、c、d、e，

　　

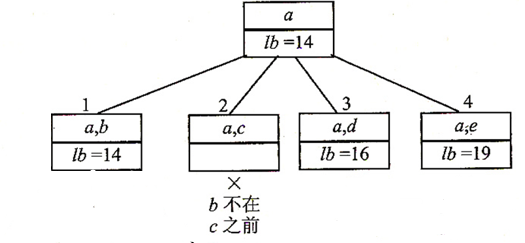
　　这里有一个小细节，就是图中的 2 节点。想想如果周游路线 a<->b<->d<->e<->a 和 a<->e<->d<-><->c<->b<->a ，这两条路线其实是一样的，但是如果不加处理的话，可能两条路线会在搜索的时候都被搜索过，这样浪费了时间。因此，我们这里做个小约定，约定 b 要在 c 之前出现。因此，图中节点 2 就被抛弃了。

　　继续上面的，从 a 走到那些点后，怎么计算理想代价呢，也就是说怎么计算 lb 呢。

　　我们用 a 到 d 来举例子吧。

　　最开始 lb 是选取每个点的代价最小的两条路， lb=[(a<->c+a<->b)+(b<->a+b<->c)+(c<->a+c<->e)+(d<->e+d<->c)+(e<->c+e<->d)]/2。a 走的是c 和 b 这两个，d 走的是e 和 c 。

　　现在我们选择 a<->d ，那 d 的一条路要被改成 a 了。我们选择将原来的 a<->b 改成 a<->d，因为要使代价最小，所以选择代价大的来替换。那么 d<->c 就被替换成 d<->a了。这时再计算就可以得到新的 lb 了。　　

　　我们应该选择 lb 最小的往下搜索，较大的等下再搜索。于是

　　

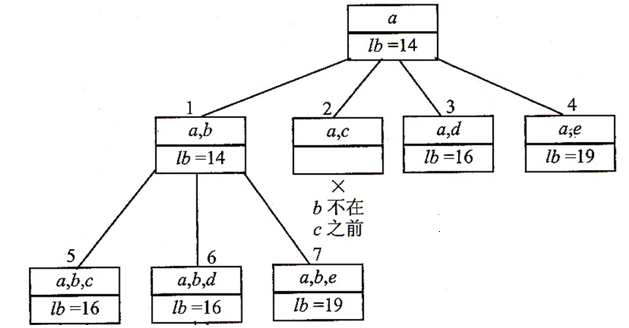
　　继续向下

　　

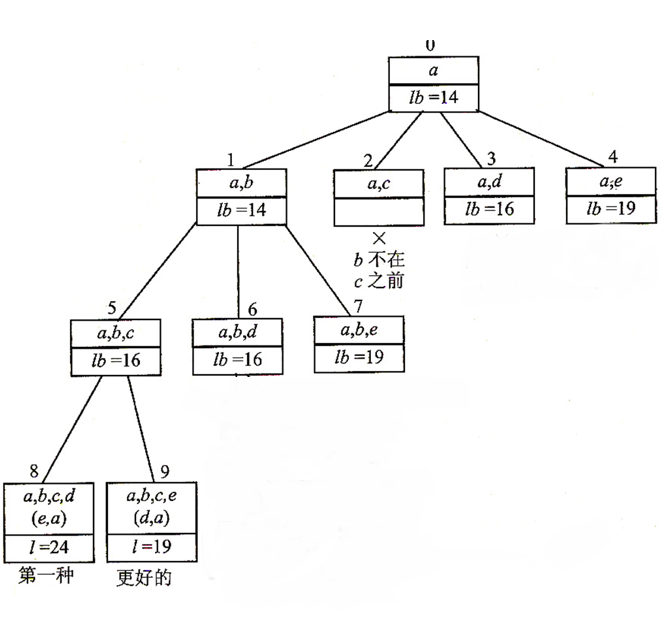
　　这时已经找出两个周游路程了（因为最后肯定要回到 a 就没向下画了），我们继续搜索，看看有没再好点的解。向上退一层，就是 节点 6 了，所以

　　

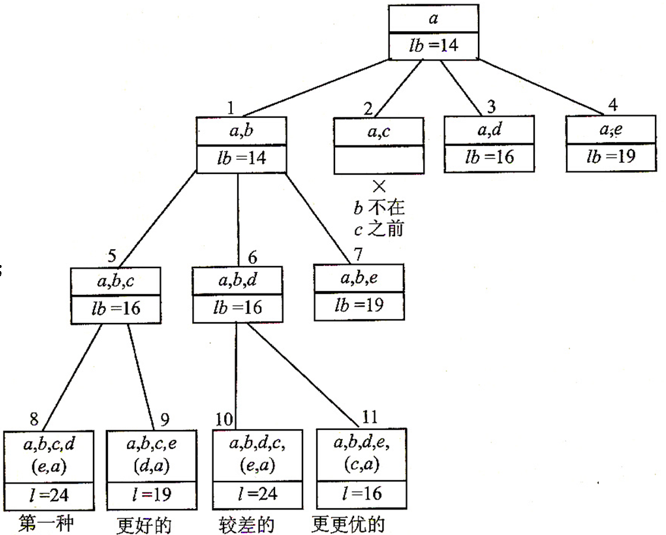
　　继续搜索，发现节点 7 才走到 e 就要 19，而 节点 11 走完了只需要 16，所以把它抛弃，继续退回，发现 3，4 都不行

　　

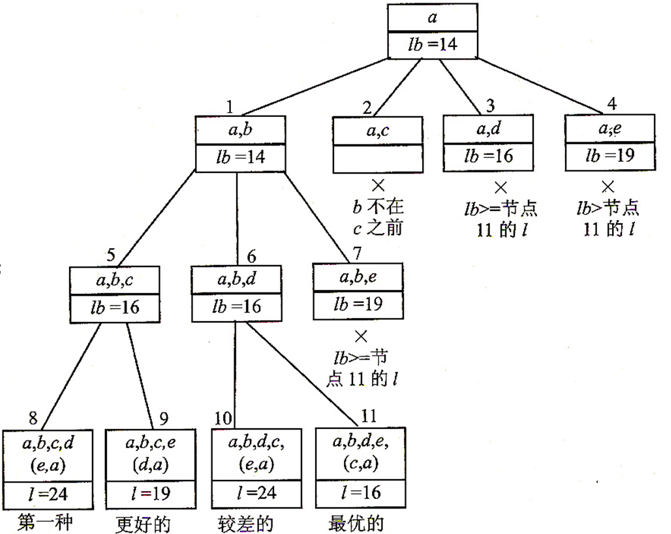
　　得到了最优解。

　　

代码：

　　代码我不会写，哈哈哈哈哈哈哈哈哈。。。。