数据挖掘之聚类算法K-Means总结

序

　　由于项目需要，需要对数据进行处理，故而又要滚回来看看paper,做点小功课，这篇文章只是简单的总结一下基础的Ｋmeans算法思想以及实现；

正文：

1.基础Kmeans算法.

　　Kmeans算法的属于基础的聚类算法，它的核心思想是：　从初始的数据点集合，不断纳入新的点，然后再从新计算集合的“中心”，再以改点为初始点重新纳入新的点到集合，在计算”中心”，依次往复，直到这些集合不再都不能再纳入新的数据为止.

图解：

　　　　假如我们在坐标轴中存在如下Ａ,B,C,D,E一共五个点，然后我们初始化（或者更贴切的说指定）两个特征点（意思就是将五个点分成两个类），采用欧式距离计算距离.

　　

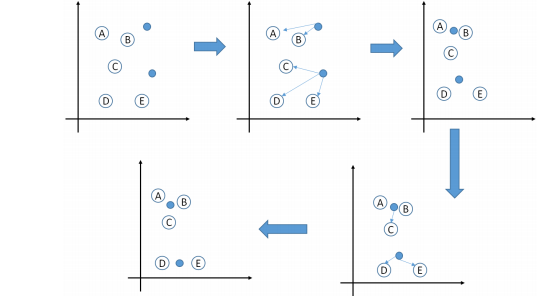
注意的点：

　　　　１．中心计算方式不固定，常用的有使用距离（欧式距离，马式距离，曼哈顿距离，明考斯距离）的中点，还有重量的质心，还有属性值的均值等等，虽然计算方式不同，但是整体上Kmeans求解的思路相同.

　　　　２．初始化的特征点（选取的Ｋ个特征数据）会对整个收据聚类产生影响.所以为了得到需要的结果，需要预设指定的凸显的特征点，然后再用Kmeans进行聚类.

代码实现：　　

 package com.data.algorithm;

 import java.util.ArrayList;
 import java.util.List;

 /**
  * *********************************************************
  * <p/>
  * Author:     XiJun.Gong
  * Date:       2017-01-17 15:57
  * Version:    default 1.0.0
  * Class description：
  * <p/>
  * *********************************************************
  */
 public class Kmeans {
     private final double exp = 1e-6;

     private List<KMeanData> topk;

     public List<KMeanData> getTopk() {
         return topk;
     }

     public void setTopk(List<KMeanData> topk) {
         this.topk = topk;
     }

     class KMeanData {

         private float x;    //x坐标
         private float y;    //y坐标
         private int flag;   //隶属于哪一个簇

         public int getFlag() {
             return flag;
         }

         public void setFlag(int flag) {
             this.flag = flag;
         }

         public float getX() {
             return x;
         }

         public void setX(float x) {
             this.x = x;
         }

         public float getY() {
             return y;
         }

         public void setY(float y) {
             this.y = y;
         }
     }

     public boolean max(float a, float b) {
         return a > b + exp ? true : false;
     }

     public float distance(KMeanData a, KMeanData b) {

         return (float) Math.sqrt(Math.pow(a.getX() - b.getX(), 2)
                 + Math.pow(a.getY() - b.getY(), 2));
     }

     public boolean Kequal(KMeanData a, KMeanData b) {
         if (Math.abs(a.getY() - b.getY()) < exp && Math.abs(a.getX() - b.getX()) < exp)
             return true;
         return false;
     }

     public KMeanData[] produce(int size, int range) {
         KMeanData[] kmData = new KMeanData[size];
         for (int i = 0; i < size; i++) {
             kmData[i] = new KMeanData();
             kmData[i].setX((float) (Math.random() * range));
             kmData[i].setY(((float) Math.random() * range));
             kmData[i].setFlag(0);
         }
         return kmData;
     }

     public void kprint(KMeanData[] data, final int k) {
         for (int i = 1; i <= k; i++) {
             System.out.println("第" + i + "簇集合: ( " + this.topk.get(i - 1).getX() + " , " + this.topk.get(i - 1).getY() + " )");
             for (int j = 0; j < data.length; j++) {
                 if (data[j].getFlag() == i) {
                     System.out.print("( " + data[j].getX() + " , " + data[j].getY() + " )");
                 }
             }
             System.out.println("\n");
         }
     }

     public KMeanData[] kmeans(KMeanData[] data, final int k) {
         if (null == data || data.length < 1) {
             System.out.println("data is empty");
             return null;
         }
         if (k > data.length) {
             System.out.println("k " + k + " is too larger than data size " + data.length);
             return null;
         }
        /*随机选取k个点*/
         topk = new ArrayList<KMeanData>();
         int stride = data.length / k;
         //均值步长取k的初始簇
         for (int i = 0; i < data.length; i += stride) {
             data[i].setFlag((i / stride) + 1);
             topk.add(data[i]);
         }
         //聚合
         while (true) {
             for (int i = 0; i < data.length; i++) {
                 float min = (float) 1e9, dist;
                 int pos = 0;
                 for (KMeanData kter : topk) {
                     if (!Kequal(kter, data[i]) && min > (dist = distance(data[i], kter))) {
                         min = dist;
                         pos = i;
                     }
                 }
                 data[pos].setFlag((i / stride) + 1);
             }
             //重新计算质心
             KMeanData[] ntopk = new KMeanData[k + 1];
             int[] kcnt = new int[k + 1];
             for (int i = 0; i < data.length; i++) {
                 kcnt[data[i].getFlag()]++;
                 ntopk[data[i].getFlag()] = new KMeanData();
                 ntopk[data[i].getFlag()].setX(ntopk[data[i].getFlag()].getX() + data[i].getX());
                 ntopk[data[i].getFlag()].setY(ntopk[data[i].getFlag()].getY() + data[i].getY());
             }
             for (int i = 1; i <= k; i++) {
                 ntopk[i].setX(ntopk[i].getX() / kcnt[i]);
             }
             //判断一下是否是已经收敛了
             boolean flag = false;
             for (int i = 0; i < k; i++) {
                 if (!Kequal(topk.get(i), ntopk[i + 1])) {
                     flag = true;
                     topk.set(i, ntopk[i + 1]);
                 }
             }
             if (!flag) break;
         }
         return data;
     }
 }

 package com.data.algorithm;

 /**
  * *********************************************************
  * <p/>
  * Author:     XiJun.Gong
  * Date:       2017-01-17 17:57
  * Version:    default 1.0.0
  * Class description：
  * <p/>
  * *********************************************************
  */
 public class Main {
     public static void main(String args[]) {
         Kmeans kmeans = new Kmeans();
         kmeans.kprint(kmeans.kmeans(kmeans.produce(100, 60), 10), 10);
     }
 }

 第1簇集合: ( 2.8443472 , 14.963217 )
 ( 19.135574 , 48.378784 )( 31.432192 , 17.925615 )( 4.5895605 , 11.125353 )( 2.1719377 , 22.074598 )( 14.182562 , 34.964306 )( 21.141474 , 39.34452 )( 39.017117 , 56.293888 )( 26.028856 , 36.239174 )( 27.319502 , 55.982365 )( 28.443472 , 14.963217 )

 第2簇集合: ( 0.8835429 , 18.1895 )
 ( 22.023354 , 41.003338 )( 23.229214 , 54.271046 )( 14.30185 , 48.939583 )( 2.4819863 , 27.38683 )( 11.668434 , 57.642452 )( 49.092728 , 55.405685 )( 23.38715 , 25.048647 )( 19.695707 , 45.738415 )( 26.929798 , 58.74604 )( 8.835429 , 18.1895 )

 第3簇集合: ( 0.74630326 , 45.51654 )
 ( 57.08818 , 41.345074 )( 14.97413 , 36.16043 )( 54.09579 , 36.052063 )( 24.645374 , 57.247772 )( 58.734444 , 27.05567 )( 13.617909 , 16.157734 )( 30.897354 , 31.427551 )( 33.367496 , 33.386326 )( 33.451378 , 53.20307 )( 7.4630327 , 45.51654 )

 第4簇集合: ( 1.968404 , 33.967808 )
 ( 5.487106 , 36.14787 )( 45.656933 , 17.261345 )( 28.166676 , 29.430775 )( 13.528182 , 41.53365 )( 22.37523 , 30.01359 )( 52.460278 , 1.8516384 )( 10.2530575 , 47.032955 )( 28.544668 , 41.290382 )( 22.431509 , 6.789385 )( 19.68404 , 33.967808 )

 第5簇集合: ( 1.6082747 , 29.020123 )
 ( 59.416927 , 22.173529 )( 27.72831 , 48.705555 )( 59.062904 , 27.449326 )( 6.909786 , 30.03262 )( 42.442226 , 8.278798 )( 51.15263 , 59.101868 )( 7.6760554 , 57.712944 )( 41.01523 , 56.367043 )( 55.39889 , 41.588028 )( 16.082747 , 29.020123 )

 第6簇集合: ( 3.2178578 , 4.2711926 )
 ( 0.53403753 , 21.35647 )( 50.560753 , 9.216217 )( 52.925297 , 18.846382 )( 48.62932 , 54.015606 )( 14.116821 , 35.78354 )( 1.8006643 , 44.74982 )( 39.19404 , 1.1245662 )( 43.081966 , 12.171013 )( 51.094734 , 31.339842 )( 32.178577 , 4.2711926 )

 第7簇集合: ( 4.042007 , 31.607666 )
 ( 50.17044 , 32.749535 )( 52.281467 , 46.060326 )( 34.024357 , 10.856017 )( 32.16631 , 54.869526 )( 11.773177 , 19.33069 )( 7.3901944 , 30.897972 )( 42.876205 , 0.90321934 )( 1.3056514 , 40.74958 )( 53.546345 , 43.86588 )( 40.42007 , 31.607666 )

 第8簇集合: ( 1.5596402 , 29.19249 )
 ( 43.503544 , 21.245668 )( 59.312412 , 35.47328 )( 12.452401 , 14.911624 )( 57.877514 , 46.545307 )( 9.161788 , 53.974636 )( 28.102057 , 40.347496 )( 56.39533 , 15.801934 )( 48.884666 , 50.610317 )( 32.18778 , 8.80818 )( 15.596402 , 29.19249 )

 第9簇集合: ( 2.5482278 , 36.367596 )
 ( 52.08338 , 38.900063 )( 46.13634 , 45.479736 )( 37.948357 , 56.04102 )( 27.17064 , 54.725323 )( 56.840836 , 23.867615 )( 53.052013 , 19.699564 )( 48.167595 , 33.628963 )( 5.600155 , 26.792658 )( 8.978055 , 53.935356 )( 25.482279 , 36.367596 )

 第10簇集合: ( 1.3590596 , 35.720345 )
 ( 35.742085 , 9.892197 )( 35.366455 , 47.68727 )( 6.3293104 , 39.160095 )( 11.329118 , 21.142208 )( 48.153606 , 18.321869 )( 42.181618 , 44.782696 )( 57.56768 , 30.652052 )( 26.439352 , 38.31146 )( 31.588612 , 55.974304 )( 13.590596 , 35.720345 )

2. 改进的ＫMeans算法；

　　ＫMeans算法存在很多很多的改进版，　比如有优化最开始的Ｋ个特征数据选取的，还有如何减少计算量的，这里就介绍一下最后一种变种.

2.1 Mini Batch K-Means；

Mini Batch K-Means思想核心：　在求解稳定的聚类中心时，每次随机抽取一批数据，然后进行Ｋmean计算，然后直至中心点稳定之后，在将所有的数据依据这些中心点进行分类，从而达到和ＫMeans一样的效果，同时有大大的减少了中间的计算量.

应用的范围：　在面对巨大的数据量时，可以考虑使用这种思路.

参考文献：

　　http://image.hanspub.org:8080/pdf/CSA20160900000_76874550.pdf