学习笔记：Kruscal 重构树

网上感觉没有什么很详细 + 证明的讲解啊）

前置：Kruskal 求最小生成树。

这个算法可以将一棵树 / 无向连通图重构成一颗有性质的新树。

算法可以解决一些树上瓶颈边权之类的问题，可以把需要持久化的并查集给代替掉。

设 \(f_i\) 为 \(i\) 所在联通块的根。

算法流程和 Kruskal 最小生成树的过程非常类似：

1. 将所有边按边权从小到大排序
2. 顺序遍历每条边 \((u, v, w)\)，若 \(u, v\) 已经联通跳过，否则建立一个新点 \(x\)，让 \(x\) 作为 \(f_u\) 与 \(f_v\) 的父亲（即连 \(x \Rightarrow f_u\) 和 \(x \Rightarrow f_v\) 的有向边），然后让 \(f_u = f_v = x\)。这个新点的点权是 \(w\)。

时间复杂度 \(O(m \log m + n \log n)\)。

最后，以最后一个建立的新点作为 \(rt\) ，就是一颗重构树了（下面是一个无向图联通变成重构树的例子，排序后第 \(i\) 条边的编号是 \(n + i\)，点权是红色，蓝色是新点，黑色是原来的点）。

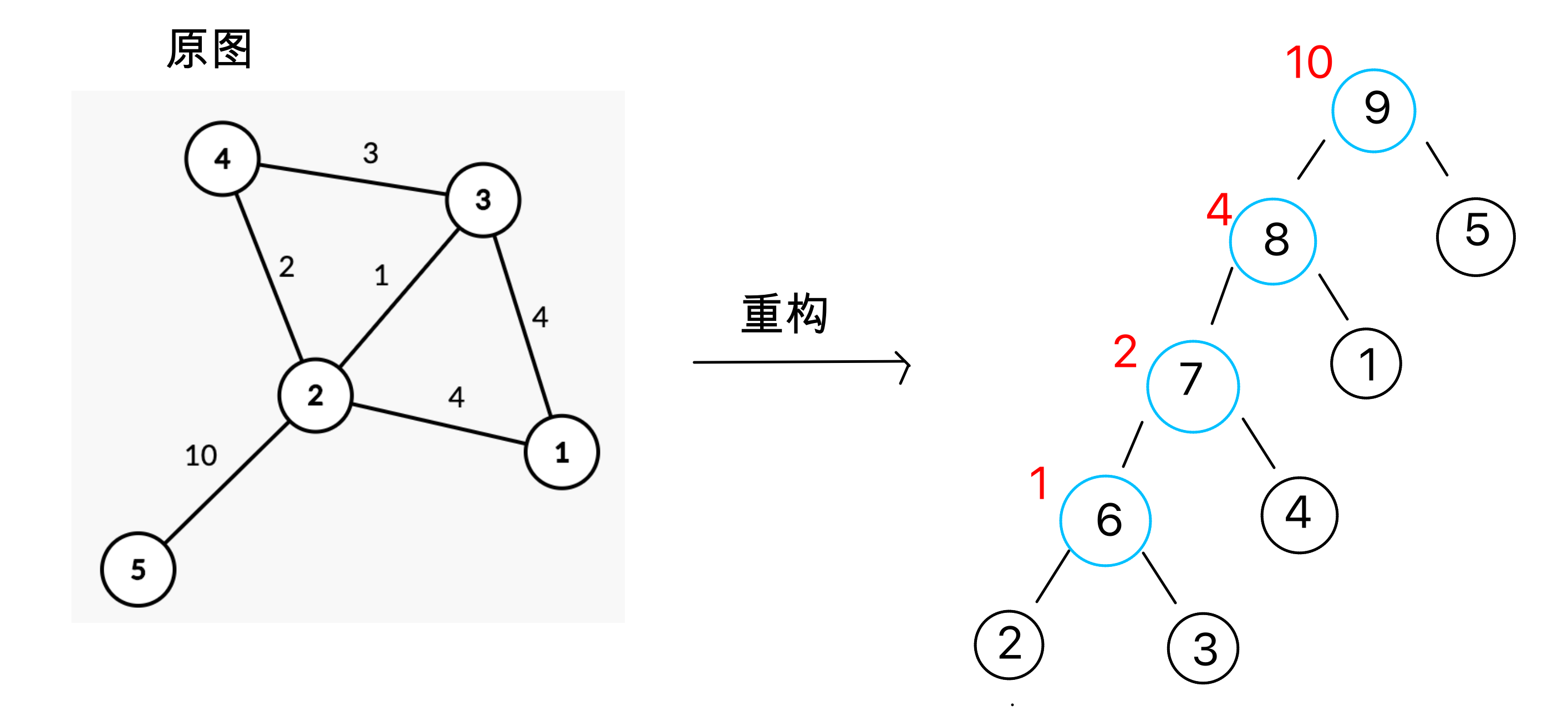
这棵树有如下性质：

• 原树若有 \(n\) 个节点，那么新树有 \(2n - 1\) 个节点，根是 \(2n - 1\)。因为建的新点就是合并两个点的次数，合并 \(n - 1\) 次。最后一次合并作为根，凑成了整个树。
• 所有原来的点就是叶子节点。因为建新图过程中我们没有让原来的点当父亲。
• 对于任意的 \(x\) 点，它的祖先链从下往上点权都是非严格递增的。因为每次合并的时候，只有 \(\le w\) 的边都构造好了，所以此时 \(f_u\) 的点权也 \(\le w\)。
• 重构树的点权是一个大根堆。跟上一个性质的等价的。
• 对于一个 \(x\) 和一个值 \(v\)。从 \(x\) 出发只经过 \(\le v\) 的边能到达的点集 \(=\) \(x\) 的祖先节点中深度最小的点权 \(\le v\) 的点 \(z\) 的子树中的原来的点集。（证明：这颗子树外的点显然不行，因为再往上点权 \(> v\)，说明再往上其他的点使通过 \(> v\) 的边才和 \(x\) 点连上的，所以不行；这颗子树内的点显然可以，因为这是一个大根堆，所以子树内的点都可以用 \(\le v\) 的边互相可达，他们在新树上的路径，经过的所有编号就是原树上经过的所有边。从这个角度，我们其实可以看作这个重构树以子树包含的形式等价于储存了 Kruscal 任何时间戳的版本。
• 对于任意 \(x, y\) ，其最小瓶颈边权（使其最大边最小的路径的最大边）为 \(x, y\) 在新树上的 LCA 点权。\(x, y\) 在经过 LCA 这条边后恰好联通，由于从小到大顺序执行，说明这条边是路径上最大的边。

如果求最大生成树，反着排序，那么偏序关系都反转，就不赘述了。

为了方便我自己创了一个名词，如果从小到大排序形成的大根堆叫 Kruscal 最小重构树，反之叫 Kruscal 最大重构树。

例题

[NOI2018]归程

预处理 \(d_i\) 表示从 \(i\) 到 \(1\) 的最短路径，这个反着建边跑最短路就行了。

问题变为：每个点有个权值，每个询问是从 \(v\) 出发经过权值 \(> p\) 的边能到的点的最小值，强制在线。

如果可以离线，那么从大到小排序边权，然后执行 Kruscal，维护一下每个联通块的最小值，每次在尝试完 merge \(>p\) 的所有边后，对应 \(O(1)\) 查询就可以了。

强制在线的话，可持久化并查集是 \(O((n + q) \log ^2 n)\) 的，是可以 过 的。

用 Kruscal 重构树的话，从大到小排序边权建 Kruscal 最大重构树，那么从 \(v\) 出发经过 \(> p\) 的边能到的点 \(=\) \(v\) 的祖先中深度最小的满足点权 \(> p\) 的点 \(x\) 的子树中所有原来的点。

由于有单调性，倍增跳就好了，子树点权最小，预处理一下就好了。

复杂度 \(O(m \log m +(n + q) \log n)\)

Code

链接

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#include <vector>
using namespace std;

typedef pair<int, int> PII;

const int N = 200005, M = 400005, INF = 2e9, L = 19;

int n, m, Q, K, S, lastans, d[N], f[N << 1], w[N << 1], val[N << 1], cnt, fa[N << 1][L];
int head[N], numE = 0;
bool vis[N];
priority_queue<PII, vector<PII>, greater<PII> > q;
struct E {
    int next, v, w;
} e[M << 1];

vector<int> g[N << 1];

struct Edge {
    int u, v, w;
    bool operator<(const Edge &b) const { return w > b.w; }
} b[M];

void inline add(int u, int v, int w) {
    e[++numE] = (E){ head[u], v, w };
    head[u] = numE;
}

void inline clear() {
    memset(head, 0, sizeof head);
    memset(fa, 0, sizeof fa);
    numE = lastans = 0;
    for (int i = 1; i < 2 * n; i++) g[i].clear();
}

void inline dijkstra() {
    for (int i = 1; i <= n; i++) d[i] = INF, vis[i] = false;
    q.push(make_pair(d[1] = 0, 1));
    while (!q.empty()) {
        PII u = q.top();
        q.pop();
        if (vis[u.second])
            continue;
        vis[u.second] = true;
        for (int i = head[u.second]; i; i = e[i].next) {
            int v = e[i].v;
            if (d[u.second] + e[i].w < d[v]) {
                d[v] = d[u.second] + e[i].w;
                q.push(make_pair(d[v], v));
            }
        }
    }
}

int find(int x) { return x == f[x] ? x : f[x] = find(f[x]); }

void inline kruscal() {
    sort(b + 1, b + 1 + m);
    for (int i = 1; i < 2 * n; i++) f[i] = i;
    for (int i = 1; i <= m; i++) {
        int u = find(b[i].u), v = find(b[i].v);
        if (u == v)
            continue;
        ++cnt;
        g[cnt].push_back(u), g[cnt].push_back(v);
        f[u] = f[v] = cnt, w[cnt] = b[i].w;
    }
}

void dfs(int u) {
    val[u] = u <= n ? d[u] : INF;
    for (int i = 1; i < L && fa[u][i - 1]; i++) fa[u][i] = fa[fa[u][i - 1]][i - 1];
    for (int i = 0; i < g[u].size(); i++) {
        int v = g[u][i];
        if (v == fa[u][0])
            continue;
        fa[v][0] = u;
        dfs(v);
        val[u] = min(val[u], val[v]);
    }
}

int main() {
    freopen("return.in", "r", stdin);
    freopen("return.out", "w", stdout);
    int T;
    scanf("%d", &T);
    while (T--) {
        scanf("%d%d", &n, &m);
        cnt = n;
        for (int i = 1, u, v, l, a; i <= m; i++) {
            scanf("%d%d%d%d", &u, &v, &l, &a);
            add(u, v, l), add(v, u, l);
            b[i] = (Edge){ u, v, a };
        }
        dijkstra();
        kruscal();
        dfs(2 * n - 1);
        scanf("%d%d%d", &Q, &K, &S);
        while (Q--) {
            int v, p;
            scanf("%d%d", &v, &p);
            v = (v + K * lastans - 1) % n + 1;
            p = (p + K * lastans) % (S + 1);
            for (int i = L - 1; ~i; i--)
                if (fa[v][i] && w[fa[v][i]] > p)
                    v = fa[v][i];
            printf("%d\n", lastans = val[v]);
        }
        if (T)
            clear();
    }
    return 0;
}