题解-[WC2011]最大XOR和路径

[WC2011]最大XOR和路径

给一个 \(n\) 个点 \(m\) 条边（权值为 \(d_i\)）的无向有权图，可能有重边和子环。可以多次经过一条边，求 \(1\to n\) 的路径的最大边权异或和。

数据范围：\(1\le n\le 5\cdot 10^4\)，\(1\le m\le 10^5,0\le d_i\le 10^{18}\)。

---

非常神的一题，令小蒟蒻大开眼界。

一句话题解：通过 \(\texttt{Dfs}\) 得到到每个点的一种路径答案，用线性基找到最优替换方案。

---

先看这个奇奇怪怪的样例，样例解释中的最优路径等价于 \(1\to2\to5\to3\to4\to5\)：

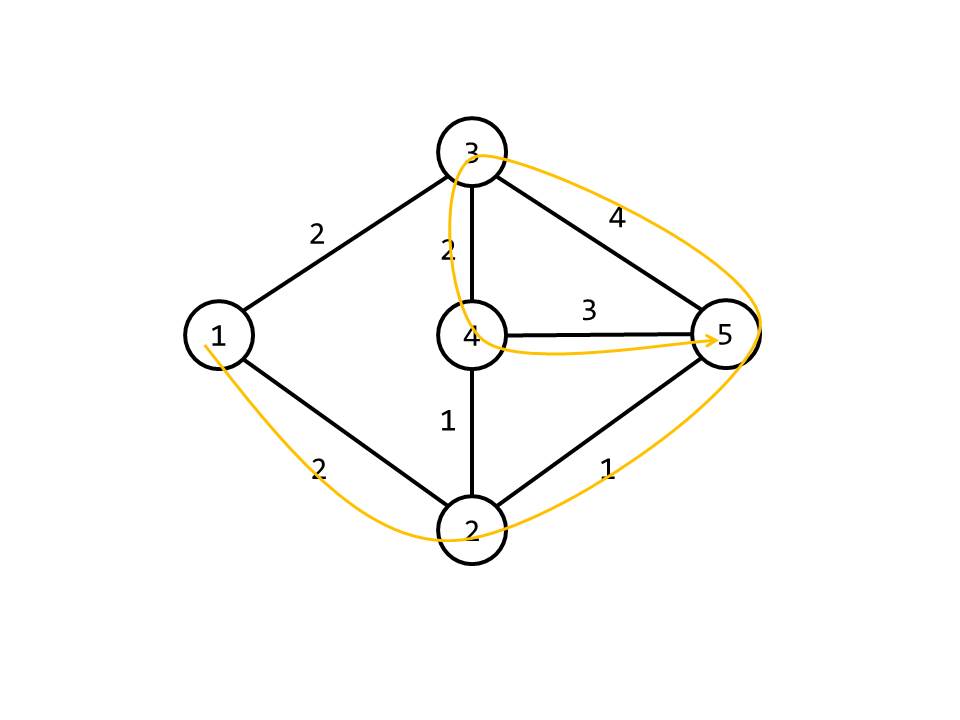
答案为 \(2\oplus1\oplus4\oplus2\oplus3=6\)。

---

有一种非常野蛮的做法是暴力 \(\texttt{Dfs}\) 整张无向图对每种答案求值，正确但是太慢。

但是考虑到异或运算的交换律，这是可以优化的，比如下图：

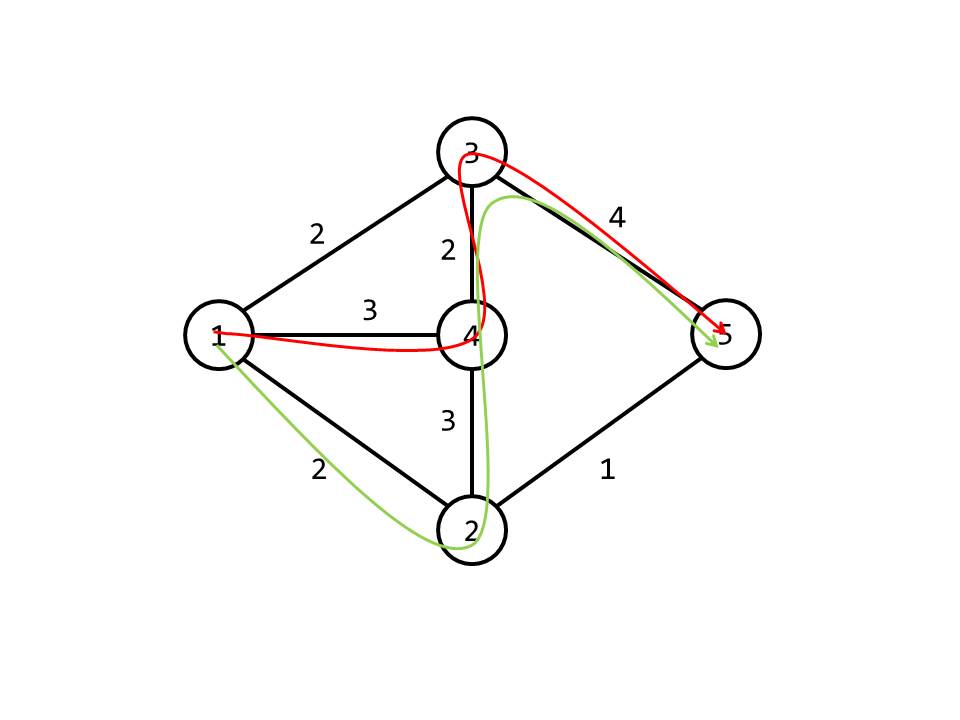
为了更好地说明问题，蒟蒻改了改样例图。

两条路径：

\(1\to4\to2\to3:3\oplus2\oplus4=5\)

\(1\to2\to4\to3\to5:2\oplus3\oplus2\oplus4=7\)

它们在 \(4\) 号点以后重合。根据异或的交换律和 \(x\oplus x=0\) 的性质可以得出两条路径的异或差（就是异或值）等于两条路径在 \(4\) 号点前的异或差。

即 \((3\oplus2\oplus4)\oplus(2\oplus3\oplus2\oplus4)=(3)\oplus(2\oplus3)=2\)

所以可以在 \(4\) 号点上记录下这个异或差 \(2\)，然后选择一条路径继续走。等找到了其中一种到 \(n\) 的路径的异或和为 \(firstans\) 时，再看看 \(firstans\) 和 \(firstans\oplus2\) 谁大，如果 \(firstans<firstans\oplus2\) 则表示选到 \(4\) 号点的另一条路径更好。

于是这样遍历图就不需要遍历重复的点了，但是会在 \(\texttt{Dfs}\) 路径的交点处留下一堆异或差。

若留下了 \(k\) 个异或差标记 \(c_i\)，则答案有 \(2^k\) 种可能性。这时可以用一个线性基把所有异或差存起来，然后把 \(firstans\) 带进去得到最优答案。

---

小蒟蒻讲不清楚，所以再拿样例来解释：

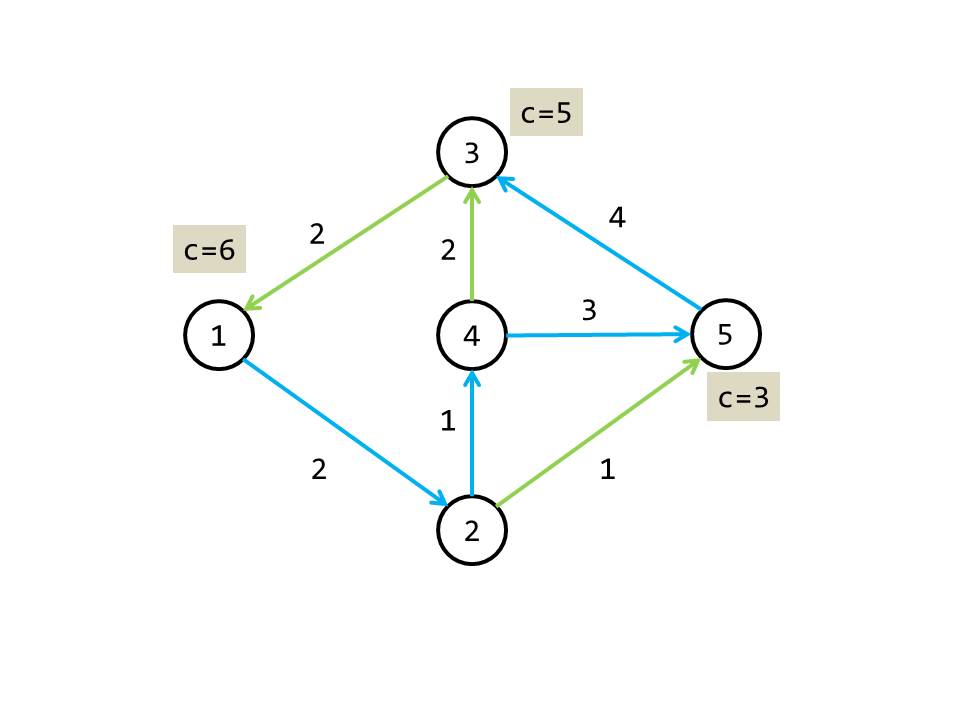
蓝色路径为 \(\texttt{Dfs}\) 树，正好是条链。

\(firstans=2\oplus1\oplus3=0\)，\(c_1=3\)，\(c_2=5\)，\(c_3=6\)。

丢进线性基：\(lb_0=0,lb_1=3,lb_2=5\)。

将 \(firstans=0\) 带入跑一趟，答案为 \(6\)。

---

时间复杂度 \(\Theta(m\log d)\)。

---

小蒟蒻又成功地写出了没人懂的题解，还是放代码吧：

#include <bits/stdc++.h>
using namespace std;

//Start
typedef long long ll;
typedef double db;
#define mp(a,b) make_pair(a,b)
#define x(a) a.first
#define y(a) a.second
#define b(a) a.begin()
#define e(a) a.end()
#define sz(a) int((a).size())
#define pb(a) push_back(a)
const int inf=0x3f3f3f3f;
const ll INF=0x3f3f3f3f3f3f3f3f;

//Data
const int N=5e4,M=2e5;
int n,m;
int E=-1;
vector<int> to;
vector<ll> w;
vector<int> e[N+7];
void add(int u,int v,ll d){
	e[u].pb(++E),to.pb(v),w.pb(d);
	e[v].pb(++E),to.pb(u),w.pb(d);
}

//LB
const int LOGA=60;
ll lb[N+7];
void add(ll x){ //logn
	for(int i=LOGA;i>=0;i--)if(x>>i){
		if(lb[i]) x^=lb[i];
		else return void(lb[i]=x);
	}
}
ll find(ll x){ //logn
	for(int i=LOGA;i>=0;i--)
		if((x^lb[i])>x) x^=lb[i];
	return x;
}

//Bfs
int vis[N+7];
ll firstans[N+7];
void Dfs(int u,ll x){
	vis[u]=1,firstans[u]=x;
	for(int i:e[u])
		if(!vis[to[i]]) Dfs(to[i],x^w[i]);
		else add(firstans[to[i]]^(x^w[i])); //遇到交点，记录异或差
}

//Main
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		int u,v; ll d;
		scanf("%d%d%lld",&u,&v,&d);
		add(u,v,d);
	}
	Dfs(1,0);
	printf("%lld\n",find(firstans[n])); //得到一种路径异或和，替换寻优
	return 0;
}

---

祝大家学习愉快！