回文树（回文自动机）（PAM）

第一个能看懂的论文：国家集训队2017论文集

这是我第一个自己理解的自动机（AC自动机不懂KMP硬背，SAM看不懂一堆引理定理硬背）

参考文献：2017国家集训队论文集回文树及其应用翁文涛

参考博客：回文树

一些定义

（回文）子串不包括空串。
（回文）后缀不包括原串本身，如果找不到，就是空串。
定义 $len[cur]$ 为 $cur$ 节点的代表串长度，$son[p][c]$ 表示一条转移路径，$fail$ 表示失配指针。
定义 $\Sigma$ 为字符集大小。
$c$ 通常表示字符，$s$ 或者 $S$ 通常代表字符串，$p,cur$ 代表节点。
有时我可能会将“回文串”和“回文树上代表其的节点”混用。

回文树原理及构造

回文树的结构

回文树由两棵树组成，一棵奇树，一棵偶树。

每个节点代表恰好一个回文串，每个原串的回文子串恰好有一个对应节点。

奇树上的点长度都为奇数，偶树上的点长度都为偶数。特别地，奇树根节点（通常编号为1）的长度为 -1，偶树根节点（通常编号为0）的长度为 0.

每个点都有一个 $fail$ 指针，指向当前串的最长回文后缀。众多 $fail$ 构成一棵以 1 为根的 $fail$ 树，其中父亲为儿子的最长回文后缀；满足 $len[fa] < len[son]$；并且一个回文串的所有回文后缀为从该节点到根节点 1 所经过的链上 $len$ 为正数的回文串。

节点数和转移（边）数

可以证明，一个字符串的本质不同的回文子串数量不超过字符串长度，因此回文树节点数为 $O(|s|)$。证明如下:

考虑新加入一个字符 $c$ 所新增的位置不同的回文子串：$s[l_1, n], s[l_2, n], ...$，那么除了 $s[l_1, n]$ 外，其它的回文子串在之前一定已经出现过了（如图）。因此加 $c$ 新增的本质不同的回文子串一定是 $s[1, n]$ 的最长回文后缀。

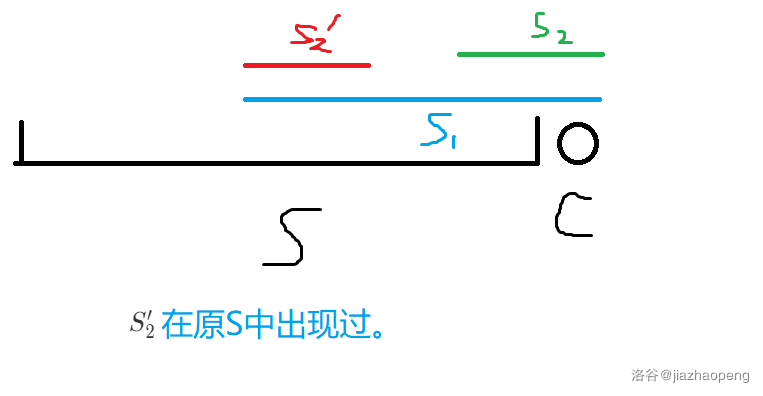
由于每个节点最多只由一个节点转移过来，因此回文树有 $O(|S|)$ 边。$fail$ 树上的边显然也是 $O(|S|)$。

构造

增量法。

显然，每次我们只需搞出当前串的最长回文后缀即可。由于当前的最长回文后缀一定是先前的一个回文后缀加一个字符，我们可以直接在先前的最长回文后缀上暴跳 $fail$ 链，直到合法位置（$s[i - 1 - len[p]] == s[i]$)。显然这是一定合法的，因为 $fail~tree$ 的根节点长度为 -1，而 $s[i - 1 - (-1)] == s[i]$ 一定成立。

然后再用类似的方法搞出当前点的 $fail$ 指针（最长回文后缀).$len, son$ 随便维护一下即可。

值得注意的是，每添加一个字符，最多只会改 $fail, len, son$ 数组中的一个位置。

关键代码

int son[N][26], fail[N], lst, len[N], tot;

inline void init() {

	len[1] = -1;

	fail[1] = fail[0] = tot = 1;

}

inline int ins(int pos, int c) {

	int p = lst;

	while (s[pos - 1 - len[p]] != s[pos])	p = fail[p];

	if (son[p][c]) return Len[lst = son[p][c]];

	int np = ++tot, x = fail[p];

	while (s[pos - 1 - len[x]] != s[pos])	x = fail[x];

	fail[np] = son[x][c];

	len[np] = len[p] + 2;

	son[p][c] = np;

	return Len[lst = np];

}

复杂度

分析一下时间复杂度。势能分析瞎搞搞就可以了。我们死盯一个量：当前的节点在 $fail~tree$ 上的深度。我们发现，每跳一次 $fail$ 这个值会减一；每插入一个字符，这个值会加一。这个值始终非负，而最多加了 $|S|$。因此时间复杂度是 $O(|S|)$ 的。

因此，时间 $O(|S|)$，空间 $O(|S|\Sigma)$。

如果 $\Sigma$ 比较大，可以使用 $map$ 存储 $son$，时间 $O(|S|log\Sigma)$，空间 $O(|S|)$

拓展

支持前后加字符

题目：hdu 5421 Victor and String

与向后加字符类似，我们可以维护最长回文后缀的指针 $fail'$，形成两棵 $fail~tree$ 。并且我们发现一个神奇的性质：如果一个回文串 $t$ 的最长回文后缀为 $t[i...|t|]$，那么根据回文串的对称性，其最长回文前缀为 $t[1...|t|-i+1]$，并且这两个回文串是一样的。也就是说， $fail$ 指针和 $fail'$ 指针指向的是同一个节点 ！那么我们就方便很多了，只需要多维护个 $lst$，前后插入字符的同时都维护一下 $fail$ 指针，整棵树的形态就是对的。

唯一一点需要注意的是，我们在前面插入一个字符 $c$，最当前串的最长回文后缀可能产生影响，当且仅当插入 $c$ 后整个串是一个回文串（显然）。因此注意修改后缀的 $lst$。后面插入对前缀的影响同理。