Learning Web Performance with MDN

Learning Web Performance with MDN

Web 性能是客观的衡量标准，是加载时间和运行时的感知用户体验。

https://developer.mozilla.org/en-US/docs/Web/Performance

Lazy loading

懒加载 / 延迟加载

https://developer.mozilla.org/zh-CN/docs/Web/Performance/Lazy_loading

延迟加载(懒加载) 是一种将资源标识为非阻塞（非关键）资源并仅在需要时加载它们的策略。

懒加载是一种缩短关键渲染路径长度的方法，可以缩短页面加载时间。

延迟加载可以在应用程序的不同时刻发生，但通常会在某些用户交互（例如滚动和导航）上发生。

随着网络的发展，我们已经看到发送给用户的资产数量和规模都在急剧增加。

从2011年到2019年，台式机的资源中位数从 ~100KB 增至 ~400KB，移动版的资源中位数从 ~50KB 增至 ~350KB。

图像大小已从台式机上的 ~250KB 增至 ~900KB，而移动设备上的 ~100KB 增至~850KB。

Critical Rendering Path / CRP

关键渲染路径

https://wiki.developer.mozilla.org/zh-CN/docs/Web/Performance/Critical_rendering_path

关键渲染路径是浏览器将 HTML，CSS 和 JavaScript 转换为屏幕上的像素所经历的步骤序列。

优化关键渲染路径可提高渲染性能。关键渲染路径包含了 文档对象模型 (DOM)，CSS 对象模型 (CSSOM)，渲染树和布局。

在解析 HTML 时会创建文档对象模型。

HTML 可以请求 JavaScript，而 JavaScript  反过来，又可以更改 DOM。

HTML 包含或请求样式，依次来构建 CSS 对象模型。浏览器引擎将两者结合起来以创建渲染树。

布局确定页面上所有内容的大小和位置。确定布局后，将像素绘制到屏幕上。

优化关键渲染路径可以缩短首次渲染的时间。

了解和优化关键渲染路径对于确保重排和重绘可以每秒 60 帧的速度进行，以确保高效的用户交互并避免讨厌是很重要的。

https://developer.mozilla.org/zh-CN/docs/Glossary/render_tree ???

CSSOM

CSS 对象模型

https://developer.mozilla.org/zh-CN/docs/Glossary/CSSOM

CSS 对象模型 (CSSOM) 是树形形式的所有CSS选择器和每个选择器的相关属性的映射，具有树的根节点，同级，后代，子级和其他关系。

CSSOM 与 文档对象模型(DOM) 非常相似。两者都是关键渲染路径的一部分，也是正确渲染一个网站必须采取的一系列步骤。

CSSOM 与 DOM一起构建渲染树，浏览器依次使用渲染树来布局和绘制网页。

CSSOM API, CSS 对象模型也是一组API，允许从J avaScript 操纵 CSS。

它非常类似于DOM，但应用于 CSS 而不是 HTML。

它允许用户动态读取和修改 CSS样式。

DOM

文档对象模型

https://developer.mozilla.org/zh-CN/docs/Glossary/DOM

refs

Web Page Performance Test / 网页性能测试

https://webpagetest.org/

https://www.xgqfrms.xyz

---

---

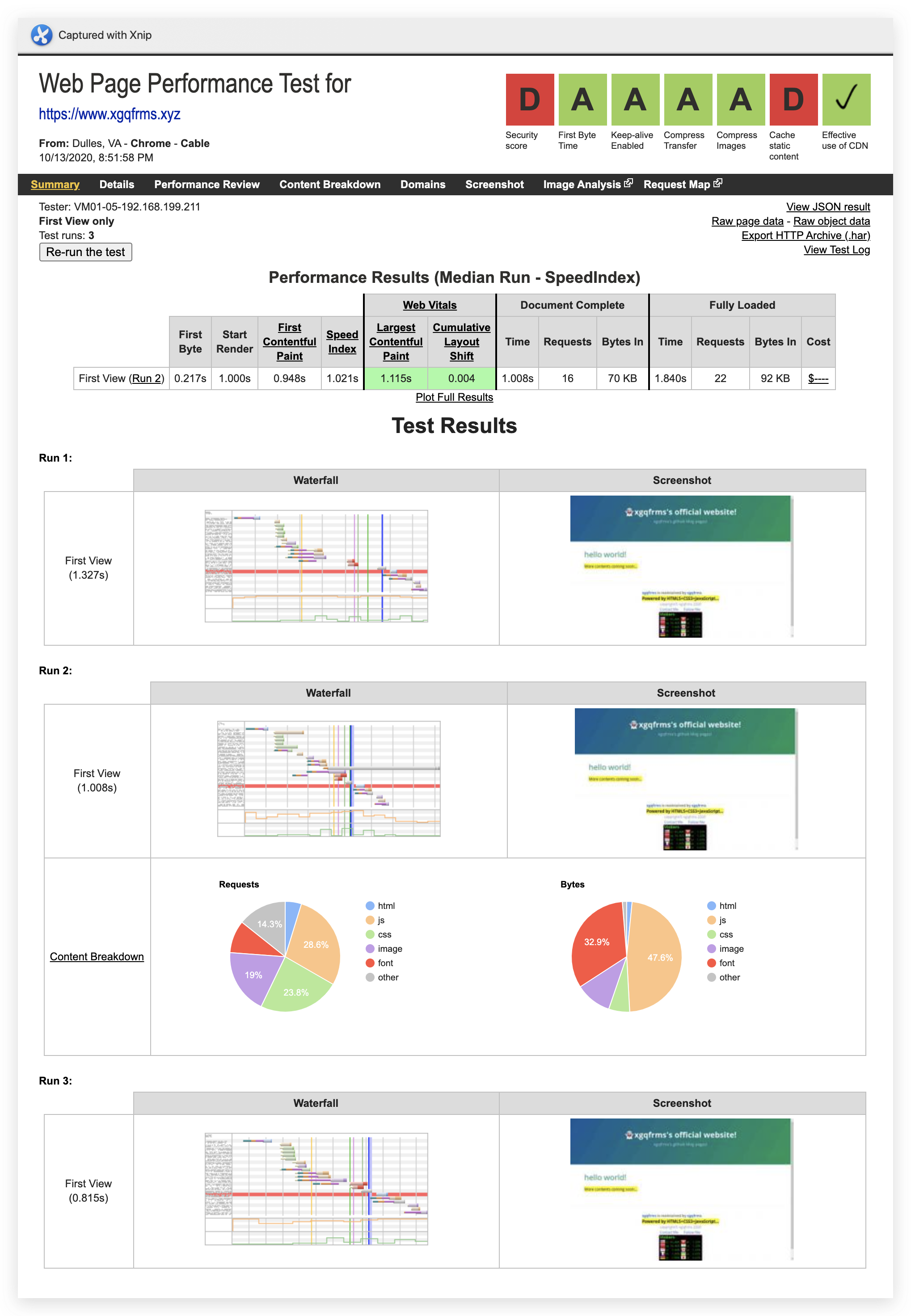
xgqfrms 2012-2020

www.cnblogs.com 发布文章使用：只允许注册用户才可以访问！

---