线性代数中的线性方程组(chapter 1)

线性代数中的线性方程组

线性代数中的线性方程组

第一章从线性方程组的角度，通过解线性方程组，开始解释数学矩阵，以及和线性代数的联系

线性方程组

形如$a_1x_1+a_2x_2+a_3x_3+....+a_nx_n=b$,其中$a_1...a_n$为实数或者复数。

对于一个线性方程组，所有可能的解称为他的解集，如果两个方程组，具有相同的解集，那么我们说这两个方程组等价的。

对于一个线性方程组，他的解有三种情况：

无解
有唯一解
有无穷多的解

如果对于一个线性方程组，他有唯一解或者无穷多个解，我们称它是相容的，若无解，我们称他是不相容的。

对于一个线性方程组求解，先将它的变量隐藏起来，再将变量的每个系数写在对齐的一列中，产生的一个矩阵，我们称它为系数矩阵,将线性方程组右侧的常数加入矩阵中，我们得到了增广矩阵.

$
\begin{cases}
x_1-2x_2+x_3=0\\
2x_2+8x_3=8\\
-4x_1+5x_2+9x_3=9
\end{cases}
$ → $\left[ \begin{matrix} 1 & -2 & 1\\ 0 & 2 & 8\\ -4 & 5 & 9\end{matrix} \right]$ → $\left[ \begin{array}{ccc|c} 1 & -2 & 1 & 0\\ 0 & 2 & 8 & 9\\ -4 & 5 & 9 & -9\end{array} \right]$

行化简解法和阶梯型矩阵

线性方程组的解法：

对于解一个线性方程组，通常的做法是将其化为等价的更简单的线性方程组。(也是基本思路)。在上一小节中，将一个线性方程组的系数提出化为了增广矩阵。接下来将采用行化简算法，去将一个矩阵先变化为与原矩阵等价的阶梯形矩阵，再变成简化行阶梯形矩阵。

那么，什么是阶梯形矩阵，什么又是简化行阶梯形矩阵？

首先先明确2个意义：

1.矩阵中的非零行和列是指，矩阵中至少包含一个非零元素的行或列。

2.非零行的先导元素是指该行最左边的非零元素。

满足以下三个条件的矩阵定义为阶梯形：

1.所有非零行在所有全零行的上面（即全零行都在矩阵的底部）。

2.非零行的先导元素比上面行的先导元素更靠右。

3.先导元素所在列，在该先导元素下面的元素都是零。

还满足以下两个条件的阶梯型矩阵可称为简化阶梯形：

4.所有非零行的先导元素为1。

5.所有非零行仅有先导元素。

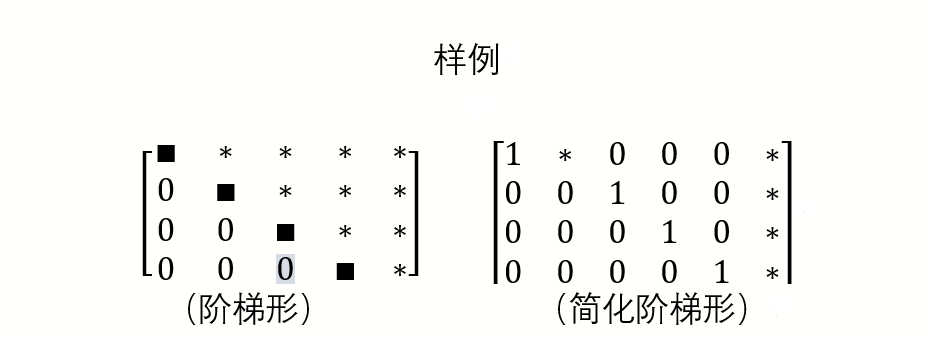
(∎表示先导元素，*表示可以是任意数字)

线性方程组的解：

对一个增广矩阵运用行化简算法时，通过将其化为等价的简化阶梯形后，可以得到线性方程组解题的一种显示表达法，例如某一个线性方程组的增广矩阵已经化为简化阶梯形

$\left[ \begin{matrix} 1 & 0 & -5 & 1\\ 0 & 1 & 1 & 4\\ 0 & 0 & 0& 0\end{matrix} \right]$
,因为增广矩阵有4列所以有3个未知数，对应线性方程组为
$\begin{cases}
x_1-5x_3=1\\
x_2+x_3=4\\
0 = 0
\end{cases}$
，对应主元列的变量$x_1$和$x_2$被称为基本变量，$x_3$被称为自由变量，当一个线性方程组是相容的，它的解集可以用显示表达，只要把方程的简化形式解出来，用自由变量表示基本变量即可。由于简化阶梯型使每个基本变量仅包含在一个方程中这是很容易解出的。
例如上面的，可得
$\begin{cases}
x_1=1-5x_3\\
x_2=4-x_3\\
x_3 为自由变量
\end{cases}$
对于自由变量$x_3$,可以是任意的值，当他的值确定后，根据前两个方程即可确定$x_1$和$x_2$。上面例子给出的解又叫通解，因为他给出了所有解的显式表达。

存在唯一性定理：

线性方程组相融的充要条件是，增广矩阵的最右列不是主元列就是说增广矩阵的阶梯形没有形如$\left[ \begin{matrix} 1 & ... & 0 & b\end{matrix} \right]$，b ≠ 0的行。若线性方程组相容，它的解集可能有两种情况：①没有自由变量时，有唯一解；②如果至少有一个自由变量有无穷多解

总结一下，对于求解一个线性方程组，可分为以下5个步骤：

1. 写出该方程的增广矩阵

2. 应用行化简算法把增广矩阵化为阶梯型，确定方程组是否有解，有解则进行下一步

3. 继续行化简算法得到它的简化阶梯形

4. 写出简化阶梯形对应的方程组

5. 将方程改写为用自由变量表示基本变量的形式

向量方程

线性方程组的重要性质都可以用向量的概念与符号来描述，该节通过将线性方程组与向量方程联系起来，解释其中的相关。

$R$²中的向量：

仅含一列的矩阵称为列向量，或简称向量如w = $\left[ \begin{matrix} w_1\\ w_2\end{matrix} \right]$，$w_1$和$w_2$是任意实数，所有2个元素的向量的集记作$R$²，其中R表示向量中的元素是实数，$2$代表一个向量包含2个元素，所有元素都为0的向量记作$0$，对于向量的加减以及标量乘法运算的性质，再初中已学过，无需赘述。

线性组合：

给定$R$ⁿ中的向量$v_1$，$v_2$，$v_3$......$v_k$和标量$c_1$，$c_2$，$c_3$......$c_k$，向量

$y$ = $c_1v_1$ + $c_2v_2$ + $c_3v_3$ + ...... + $c_kv_k$

被称作向量$v_1$，$v_2$，$v_3$......$v_k$以$c_1$，$c_2$，$c_3$......$c_k$权的线性组合，权可以是任意实数，包括零

现在我们回到前面2节中的存在性问题上，例如，给出向量$a_1$ = $\left[ \begin{matrix} 1\\ -2\\ -5\end{matrix} \right]$，$a_2$ = $\left[ \begin{matrix} 2\\ 5\\ 6\end{matrix} \right]$，$b$ = $\left[ \begin{matrix} 7\\ 4\\ -3\end{matrix} \right]$，需要确定$b$是否可以写成$a_1$和$a_2$的线性组合，也就是说，是否存在权使得向量方程 $b$ = $x_1a_1$ + $x_2a_2$ 成立。

根据向量的加法和标量乘法，可将向量方程写作方程组

$\begin{cases}
x_1+x_2 = 7\\
-2x_1+5x_2 = 4\\
-5x_1+6x_2 = -3
\end{cases}$
对上面的方程组运用行化简算法，来解出结果
$\left[ \begin{matrix} 1 & 2 & 7\\ -2 & 5 & 4\\ -5 & 6 & -3\end{matrix} \right]$ ~ $\left[ \begin{matrix} 1 & 2 & 7\\ 0 & 9 & 18\\ 0 & 16 & 32\end{matrix} \right]$ ~ $\left[ \begin{matrix} 1 & 2 & 7\\ 0 & 1 & 2\\ 0 & 1 & 2\end{matrix} \right]$ ~ $\left[ \begin{matrix} 1 & 0 & 3\\ 0 & 1 & 2\\ 0 & 0 & 0\end{matrix} \right]$
解出$x_1$ = 3和$x_2$ = 2，因此$b$就是$a_1$和$a_2$的线性组合，权为$x_1$ = 3和$x_2$ = 2，这样的步骤是为了强行通过线性方程组作为中介联系，注意看上面的例子可以看住通过线性方程组得到的增广矩阵，就是$\left[ \begin{matrix} a_1 & a_2 & b\end{matrix} \right]$。

综合上面的例子的出结论：向量方程 $x_1a_1$ + $x_2a_2$ + ...... + $x_na_n$ = $b$和增广矩阵为$\left[ \begin{matrix} a_1 & a_2 & ... & b\end{matrix} \right]$有相同的解集。当且仅当有解是，等式成立。

Span{$v_1$，$v_2$，$v_3$......$v_k$}：

线性代数的一个主要思想就是研究可以表示某一固定向量集合{$v_1$，$v_2$，$v_3$......$v_k$}的线性组合的所有向量，用Span{$v_1$，$v_2$，$v_3$......$v_k$}表示，称为由$v_1$，$v_2$，$v_3$......$v_k$生成的所有子集，也就是说Span{$v_1$，$v_2$，$v_3$......$v_k$}就是所有形如$c_1v_1$ + $c_2v_2$ + $c_3v_3$ + ...... + $c_kv_k$的向量的合集合，判断一个向量$b$是否属于Span{$v_1$，$v_2$，$v_3$......$v_k$}，就是判断$c_1v_1$ + $c_2v_2$ + $c_3v_3$ + ...... + $c_kv_k$ = $b$ 是否有解。

矩阵方程$Ax = b$

线性代数的一个基本思想就是把向量的线性组合看作是矩阵与向量的积，在本节中将上一节的某些概念用新的方法表述。

定义：

若$A$是 $m×n$的矩阵，他的各列为$a_1，...，a_n$。若$x$是$R^n$中的向量，则$A$于$x$的积，记为$Ax$，就是$A$的各列以$x$中对应元素为权的线性组合，即

$Ax = \left[ \begin{matrix} a_1 & a_2 & ... & a_n\end{matrix} \right] \left[ \begin{matrix} x_1 \\ x_2 \\ ... \\ x_n\end{matrix} \right] = x_1a_1 + x_2a_2 + ...... + x_na_n$
形如上面的式子，称为矩阵方程，注意$Ax$仅当$A$的列数等于$x$中的元素个数时才有定义。

到这里我们不难发现对于一个线性方程组，可以将其转换成向量方程，或是矩阵方程，据此我们定义。

定义：

若$A$是 $m×n$的矩阵，他的各列为$a_1，...，a_n$。而$b$属于$R^n$，则矩阵方程

$Ax = b$
与向量方程
$x_1a_1 + x_2a_2 + ...... + x_na_n = b$
有相同的解集，他又与增广矩阵为
$\left[ \begin{matrix} a_1 & a_2 & ... & b\end{matrix} \right]$
的线性方程组有相同的解集。