python 字典的用法，访问、增删合并等

python字典可以存储任意类型的对象，字典的每个键:值 冒号（:）分割，每个对直接逗号（,）分割，整个字典包含在{}中，例如：d = {key1 : value1, key2 : value2, key3 : value3 }

注：键是唯一的，值不一定，值可以是任何类型对象，键必须是不可变的，如字符串、数字

eg：

定义两个字典：

dict1 = {'time':'2021/1/28'}
dict2 = {'名字':'张三','学历':'本科','年龄':'20'}
1、字典的访问，有两种方式，添加修改
dict[key]的方式:返回可以键对应的值，如果'key'不存在，会提示key error
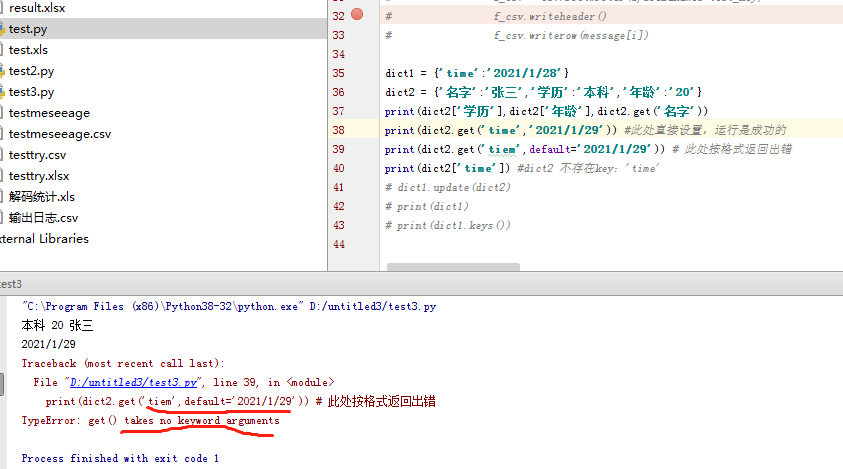
dict.get('key'，default=None):返回指定key的值，如果键不在字典中返回 default 设置的默认值 ，这个方式如果按python指定的格式dict.get(key,default='')的方式会踩雷出错，直接设置default的值或者不按默认反而不会出错，
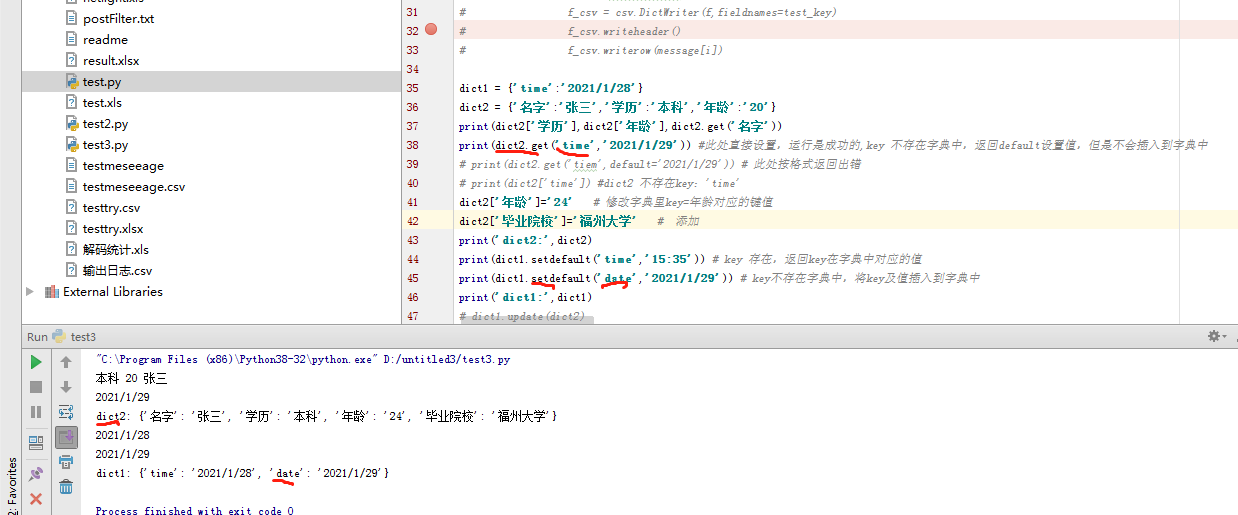
dict。setdefaul（key，default=None）：如果 key 在 字典中，返回对应的值。如果不在字典中，则插入 key 及设置的默认值 default，并返回 default ，default 默认值为 None。
关于 ：get()和setdefault()这两者的区别：主要在于当查找的键值 key 不存在的时候，setdefault()函数会返回默认值并更新字典，添加键值；而 get() 函数只返回默认值，并不改变原字典。

运行结果情况如下：

2、字典的删除：del  方法和 pop 方法

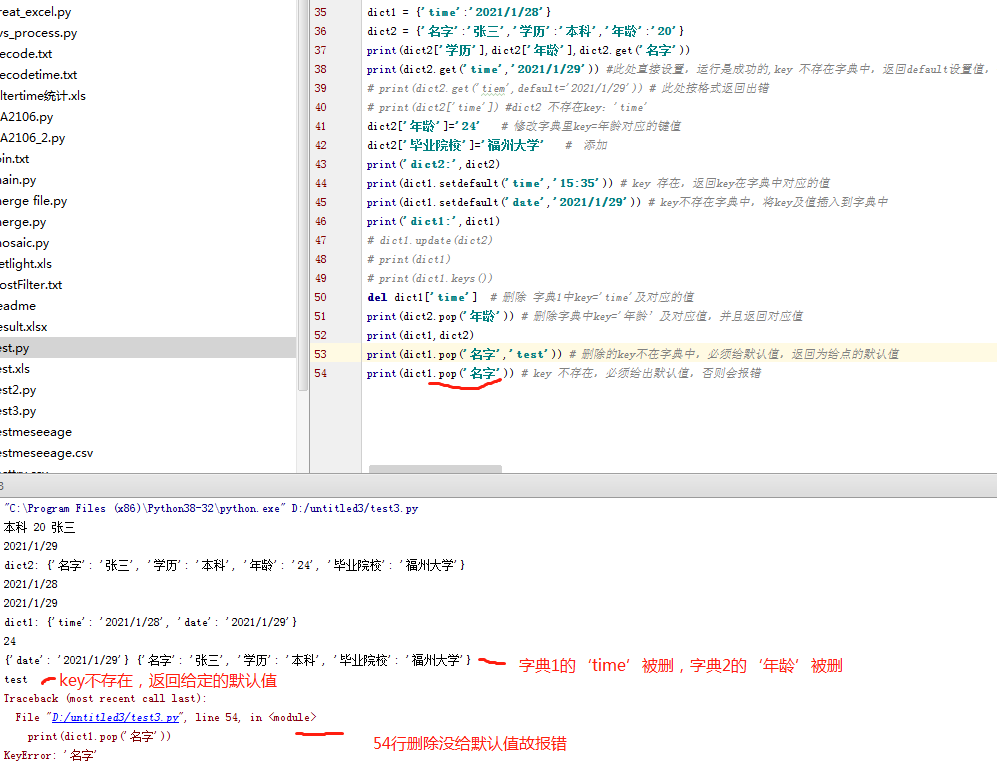
del  方法：del dict[key] 删除key及值，

pop 方法：pop(key[,default]) :删除字典给定键 key 所对应的值，返回值为被删除的值。key值必须给出。 否则，返回default值。如果要删除的 key 不存在，则需要添加默认值，否则会报错

3、字典的其他应用：

• 字典的删除：原始：dict1: {'time': '2021/1/28', 'date': '2021/1/29'}

dict1.clear() # 删除字典内所有元素
print(len(dict1),dict1) # 删除后的字典元素个数，字典
运行结果：0 {}

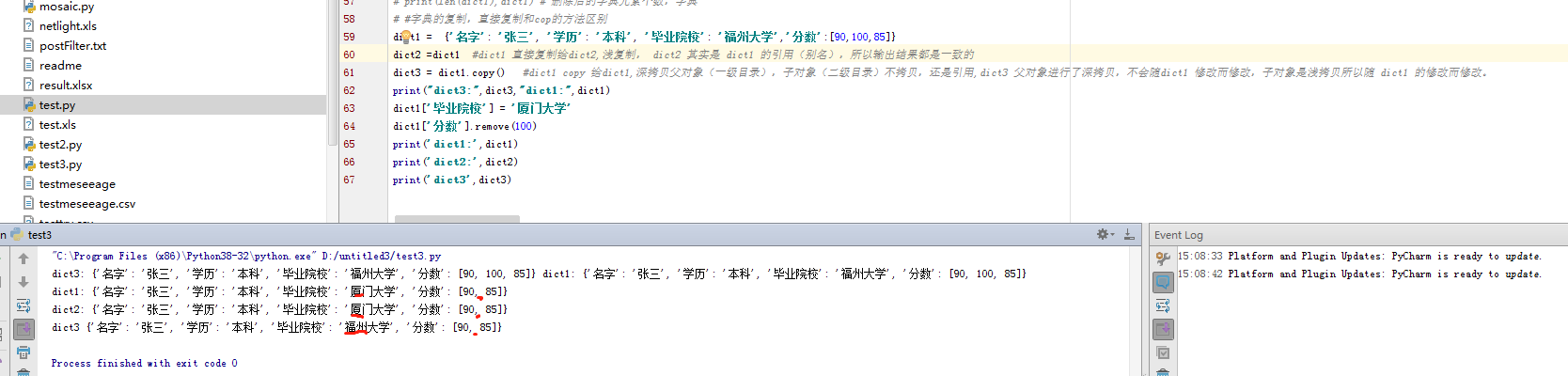
• 字典的浅复制和直接复制，二者区别：

直接赋值：浅拷贝，会随这赋值的字典的修改而修改

dict.copy()的方法： 深拷贝父对象（一级目录），不拷贝子对象（二级目录）只是引用

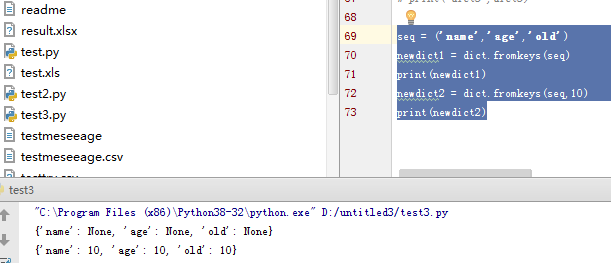
• fromkeys()函数创建一个新字典，以序列 seq 中元素做字典的键，value 为字典所有键对应的初始值。语法：

  dict.fromkeys(seq[, value])， 返回一个新的字典

  • seq -- 字典键值列表。
  • value -- 可选参数, 设置键序列（seq）对应的值，默认为 None。

  

• key in dict ：

  字典 in 操作符用于判断键是否存在于字典中，如果键在字典 dict 里返回 true，否则返回 false。

  而 not in 操作符刚好相反，如果键在字典 dict 里返回 false，否则返回 true。

• items()方法语法：以列表返回可遍历的(键, 值) 元组数组，可以用list()来转换为列表
• keys()方法语法：返回一个可迭代对象，可以使用 list() 来转换为列表。
• values() 方法返回一个迭代器，可以使用 list() 来转换为列表，列表为字典中的所有值。
• update() 函数把字典参数 dict2 的 key/value(键/值) 对更新到字典 dict 里。
•