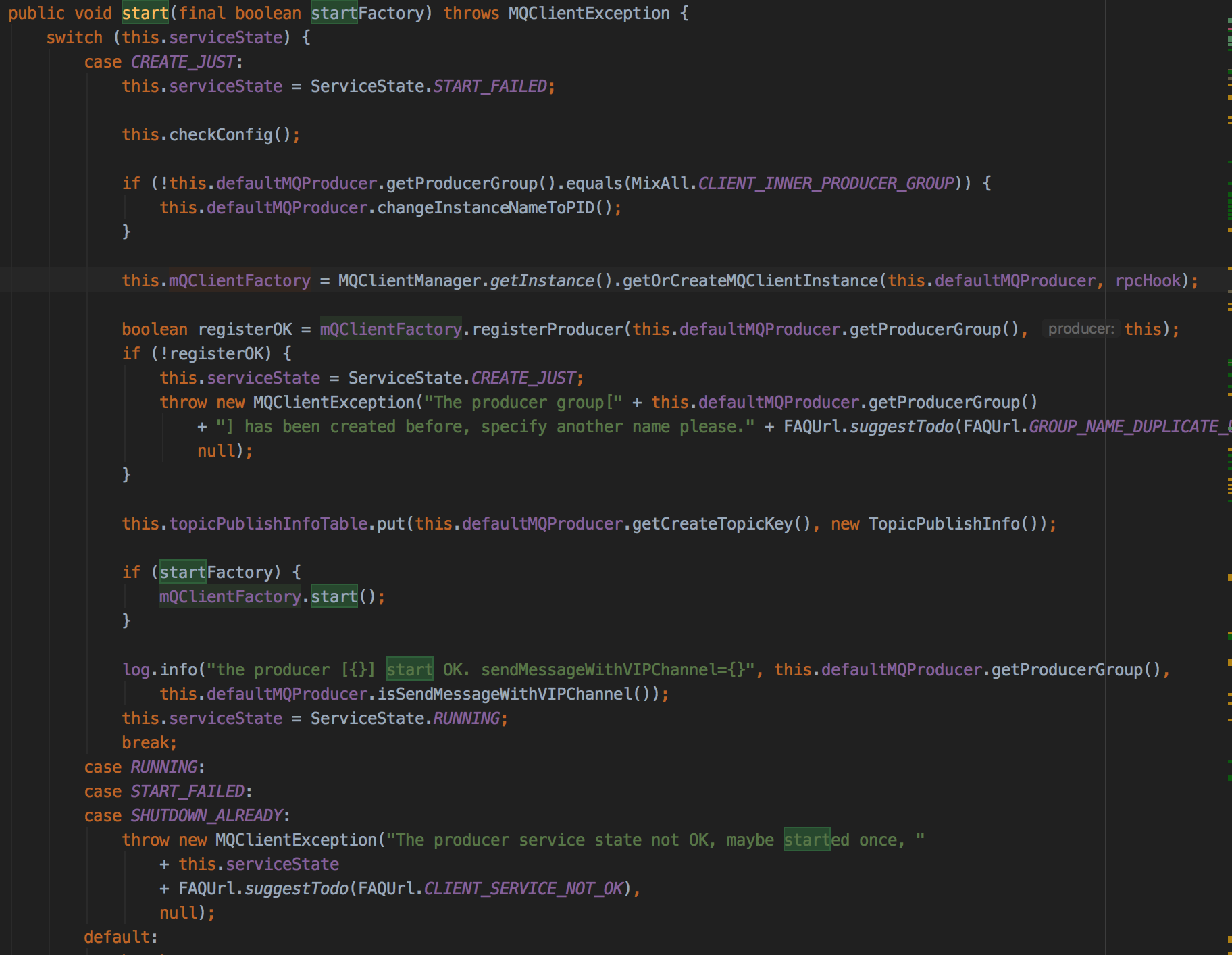
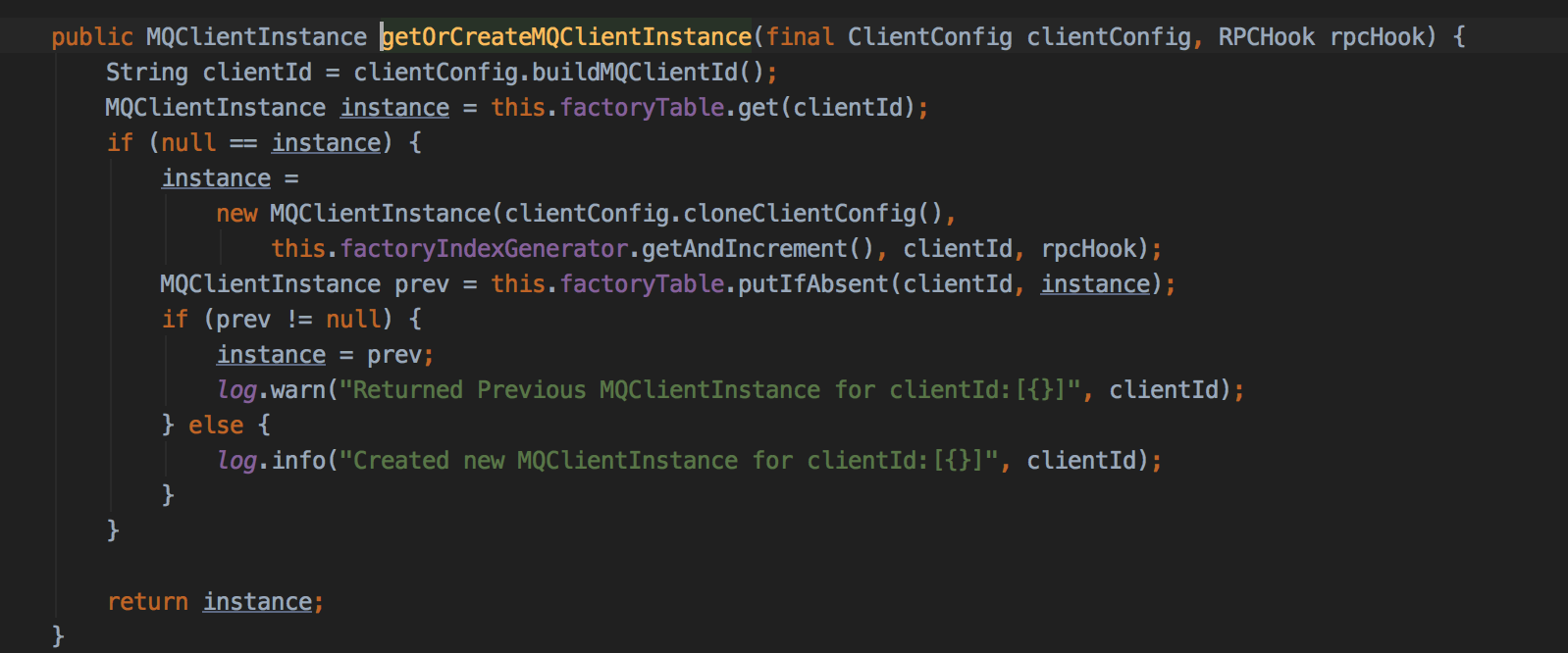
创建MQClientInstance实例。这里有个实例缓存

clienrId为客户端IP+instance+(unitname)注意到之前把instance替换为进程id，是为了instance为默认值时，同一台物理服务器部署两个应用程序。

MQClientInstance封装了RocketMQ网络处理API，是消息生产者(Producer),消息消费者与NameServer,Broker打交到的网络通道。

向MQClientInstance注册，将当前生产者加入到MQClientInstance管理中（一个ConcurrentMap），方便后续调用网络请求，进行心跳检测等。

【mq读书笔记】mq producer启动流程的更多相关文章

  1. TIJ读书笔记02-控制执行流程

      TIJ读书笔记02-控制执行流程 TIJ读书笔记02-控制执行流程 if-else 迭代 无条件分支 switch语句 所有条件语句都是以条件表达式的真假来决定执行路径,也就是通过布尔测试结果来决 ...

  2. 【mq读书笔记】如何保证三个消息文件的最终一致性。

    考虑转发任务未成功执行,此时消息服务器Broker宕机,导致commitlog,consumeQueue,IndexFile文件数据不一致. commitlog,consumeQueue遍历每一条消息 ...

  3. 【mq读书笔记】消息队列负载与重新分配(分配 新队列pullRequest入队)

    回顾PullMessageService#run: 如果队列总没有PullRequest对象,线程将阻塞. 围绕PullRequest有2个问题: 1.PullRequest对象在什么时候创建并加入p ...

  4. 【mq读书笔记】mq事务消息

    关于mq食物以什么样的方式解决了什么样的问题可以参考这里: https://www.jianshu.com/p/cc5c10221aa1 上文中示例基于mq版本较低较新的版本中TransactionL ...

  5. 【mq读书笔记】顺序消息

    注意异常情况导致整个消费无限重试 阻塞消费 mq支持局部消息顺序消费,可以确保同一个消息消费队列中的消息被顺序消费.看下针对顺序消息在整个消费过程中做的调整: 队列负载: DefaultMQPushC ...

  6. 【mq读书笔记】消息拉取

    疑问:PullRequest何时添加? PullMessageService提供延迟添加与立即添加2种方式 疑问:PullRequest是在什么时候创建的呢? 1.上上图中 PullRequest p ...

  7. 【mq读书笔记】mq消息消费

    消息消费以组的的模式开展: 一个消费组内可以包含多个消费者,每一个消费组可订阅多个主题: 消费组之间有集群模式与广播模式两种消费模式:集群模式-主题下的同一条消息只允许被其中一个消费者消费.广播模式- ...

  8. 【mq读书笔记】消息消费队列和索引文件的更新

    ConsumeQueue,IndexFile需要及时更新,否则无法及时被消费,根据消息属性查找消息也会出现较大延迟. mq通过开启一个线程ReputMessageService来准时转发commitL ...

  9. 【mq读书笔记】mq读写分离机制

    mq根据brokerName查找Broker地址的过程 mq根据MessageQueue查找Broker地址的唯一依据是brokerName,同一组Broker(M-S)他们的bokerName相同但 ...

随机推荐

  1. [论文阅读]阿里DIEN深度兴趣进化网络之总体解读

    [论文阅读]阿里DIEN深度兴趣进化网络之总体解读 目录 [论文阅读]阿里DIEN深度兴趣进化网络之总体解读 0x00 摘要 0x01论文概要 1.1 文章信息 1.2 基本观点 1.2.1 DIN的 ...

  2. socket编程：recvmsg 和 sendmsg 函数

    背景 复习 socket 编程的时候发现了以前没有留意到的 2个函数:recvmsg 和 sendmsg ref : Linux编程之recvmsg和sendmsg函数 知识 先来看看函数原型: #i ...

  3. Django前后端安全验证

    会话技术 关注公众号"轻松学编程"了解更多. 1.Cookie 客户端会话技术(数据存储在客户端) 以key-value的形式进行存储 cookie的操作都是通过Response来 ...

  4. Git clone 克隆Github上的仓库，速度慢？

    一. 终端输入: git config --global http.postBuffer 524288000 二. git替换https 三. windows 安装 https://motrix.ap ...

  5. Java中的常见数学运算

    1.舍掉小数取整:Math.floor(3.5)=3 2.四舍五入取整:Math.rint(3.5)=4 3.进位取整:Math.ceil(3.1)=4 4.取绝对值:Math.abs(-3.5)=3 ...

  6. 用微信小程序做一个小电商 sku

    效果展示图 功能点概述 图一功能点有 搜索 轮播图 商品展示 图二功能点 导航栏 加入购物车 图四功能点 评论点 图五购物车 复选框 ( 全选全不选 ) 即点即改 总计结算 功能详解 1.A(搜索) ...

  7. MSSQL 指定分隔符号 生成数据集

    DECLARE @xml VARCHAR(MAX)='磨毛:1 缩率:2 干磨:3 湿摩:4 水洗牢度:5 手感:6 防水:7 PH:8 日晒:9' SET @xml= '<root>'+ ...

  8. mysql between and 是[a,b]闭区间

    mysql between and 是[a,b]闭区间 mysql between and 是[a,b]闭区间

  9. Flutter 开发从 0 到 1（五）源码

    Flutter 开发从 0 到 1 明天开始又要上班了,你的假期任务完成如何啊?由于平时加班太多了,实在挤不出更多时间,从开始想用 Flutter <Flutter 开发从 0 到 1(一)需求 ...

  10. Linux 8个有力的Awk内建变量

    Awk 有几个非常强力的内置变量.通常来说,分为两种类型的内置变量: 第一种是定义的变量可以改变, 比如字段分隔(FS)与记录分隔(RS) 第二种是可以用来数据处理或者数据总结,比如记录数(NR)与字 ...