python 相对路径和绝对路径的区别

一，Python中获得当前目录和上级目录

获取当前文件的路径：

from os import path
d = path.dirname(__file__)  #返回当前文件所在的目录
# __file__ 为当前文件, 若果在ide中运行此行会报错,可改为  #d = path.dirname('.')

获得某个路径的父级目录:( 强烈建议使用该方法！可以逐层获取到根目录的地址，例如D：/）

parent_path = os.path.dirname(d) #获得d所在的目录,即d的父级目录
parent_path  = os.path.dirname(parent_path) ##获得parent_path所在的目录即parent_path的父级目录

获得规范的绝对路径：

abspath = path.abspath(d) #返回d所在目录规范的绝对路径

​

二，路径拼接

Python3 os.path.join（）用法

功能描述：os.path.join（）函数用于路径拼接文件路径。

语法：os.path.join（path1 [，path2 [，...]]）

os.path.join（）函数中可以传入多个路径：

1.会从第一个以“/”开头的参数开始拼接，之前的参数全部丢弃。

2.优先判定上一种情况。若无，则如果出现“./”开头的参数，会从“./”开头的参数的上一个参数开始拼接。

​

三，蟒蛇里面的相对路径与绝对路径

​

​

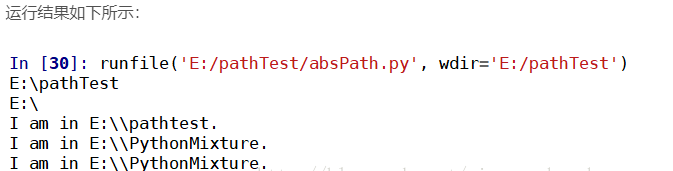
如例程所示：

os.path.abspath则则（ ''）可以获取当前脚本所在的路径，当我们需要在该目录下生成一些文件时，就可以用此命令获取脚本路径。

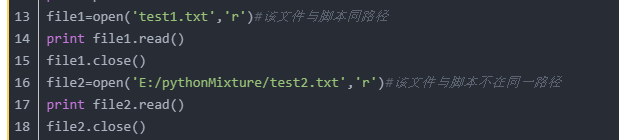
开放（ 'test1.txt的的'， 'R'）以只读的形式打开该脚本所在路径下的名为test1.txt的的文件文档。

开放（'E：/pythonMixture/test2.txt'，'R'）以只读形式打开E：/ pythonMixture路径下的的test2.txt文档

由于字符“\”为蟒蛇中的字符串转义字符，所以：

open（'E：/pythonMixture/test2.txt'，'r'）这句等价于open（'E：\\ pythonMixture \\ test2.txt'，'r'）
--------- ----

四，实战截图

目的：为了验证E：/ CRMAutoTest001 \ pre_infoChannel.csv E：\ CRMAutoTest001 \ others \上层的测试文档

这两各包含“/”和“\”的地址组合，都是正确的路径。

所以后续遇到这两种写法，都是正确的。

​

再着重记忆一遍，代码第16行，当文件与脚本不在同一路径，绝对路径的规范写法：E：/pythonMixture/test2.txt

​

​

五、小结：

1.  os.path.join（）函数用于路径拼接文件路径，这是主流常用的。 方法内部代码封装的完美，只要传入正确的两个路径即可。

2.按照MVC设计结构，相同功能的文件要存放在同个文件夹，当项目大了模块多时就会很好维护。

比如数据源文件，配置文件，公共方法文件，模块控制层文件等。

现在从事的项目，就不进行相对路径和绝对路径的优化，等新项目开始，再重新涉及开发。

3.因为项目的绝对路径都是以E盘根目录开始的，所以测试组小伙伴们从gitlab下载了仓库后，也要把仓库文件复制到E盘根目录，避免报错。

4. 后期要实现的效果，是：全都使用相对路径来配置各类地址。确保所有人从gitlab下载好的仓库文件，安装在哪个盘哪个位置都不会报地址错误（这也是为什么使用相对路径的最根本原因。）