DFS【搜索1】

DFS模板

void dfs(int depth)//depth表示当前的层数(或深度)
{
    if(depth>n)//到达叶子节点，该路已走到尽头
        return;
    for(int i=;i<=n;i++)//n表示最大的值，即最大深度为n
    {
        if(b[i]==)//b数组表示探索的状态，1表示已被探索，0表示尚未被探索
        {
            b[i]=;//标记当前的b[i]已被探索
            a[level]=i;//记录当前的节点值
            dfs(level+);//进一步的搜索
            b[i]=;//还原当前的b[i]元素被探索的状态
        }
    }
}

---

数字型搜索

---

全排列问题

题目描述

排列与组合是常用的数学方法。
先给一个正整数 ( 1 < = n < = 10 )
例如n＝3，所有组合,并且按字典序输出：
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

输入

输入一个整数n(  1<=n<=10)

输出

输出所有全排列

每个全排列一行，相邻两个数用空格隔开（最后一个数后面没有空格）

样例输入 Copy

3

样例输出 Copy

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

#include<bits/stdc++.h>
#include<queue>
using namespace std;
const int N=;
typedef long long ll;
int n,a[],b[];
void print()
{
    for(int i=;i<=n;i++)
    {
        printf("%5d",a[i]);
    }
    cout<<endl;
}
void dfs(int level)
{
    if(level==n+)
    {
        print();
        return;
    }
    for(int i=;i<=n;i++)
    {
        if(b[i]==)
        {
            b[i]=;
            a[level]=i;
            dfs(level+);
            b[i]=;
        }
    }
}
int main()
{
    cin>>n;
    dfs();
}

【牛客】 Factorial

1、暴力解题，代码略；

2、dfs解题(重点)，万物皆可搜，有点类似斐波那契递归

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll maxn=1e5+;
#define IO ios::sync_with_stdio(false), cin.tie(0)
#define T int t ;cin >> t;while(t--)
ll a[maxn];
ll dfs(ll n)
{
    if(n<=)
    {
        return ;
    }
    else
    {
        return dfs(n-)*n;
    }
}
int main()
{
    T
    {
        ll n;
        scanf("%lld",&n);
        printf("%lld\n",dfs(n));
    }
}

---

地图型搜索

---

n皇后问题

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,y[],s,ans[];
bool check(int x)//剪枝，判断两点的位置\\
两点的斜率的绝对值不得等于1；两点不得在同一水平线上(包括同一行和同一列)
{
    for(int i=;i<x;i++)//i本身就是指行号，y[i]表示对应的列号
    {
        if(abs(x-i)==abs(y[x]-y[i])||y[x]==y[i]||x==i)
        {
            return ;
        }
    }
    return ;
}
void dfs(int num)
{
    if(num>n)//越界处理
    {
        s++;
        return;
    }
    for(int i=;i<=n;i++)
    {
        y[num]=i;//将当前的行号赋值给第num个皇后
        if(check(num))
            dfs(num+);//进行下一步的搜索
    }
}
int main()
{
    for(int i=;i<=;i++)
    {
        n=i;
        s=;
        dfs();
        ans[i]=s;
    }
    while(~scanf("%d",&n)&&n)
        printf("%d\n",ans[n]);
}

POJ3083 Children of the Candy Corn

左搜索(Ldfs)+右搜索(Rdfs)+最短路径搜索(bfs)

搜索方位

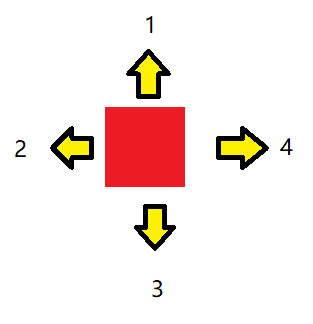
左搜索：

始终靠左搜索，如果左边是墙#，那就往上面搜索；上面是墙#，那就往右边搜索；右边是墙#则返回之前的位置，即往后搜索。

右搜索：

bfs最短路搜索：

创建队列，在一个点的周围的同一层搜索(这是与DFS的区别最大之处)，用vis数组标记是否被搜索过

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N=;
char mp[][];
int vis[][];
int m,n,f,ans1,ans2;
int head_x,head_y,tail_x,tail_y;
int dir1[][]= {-,,,,,,,-};
struct node
{
    int x,y,step;
} head,tail;
bool judge(int xx,int yy)
{
    if(xx>=&&xx<=m&&yy>=&&yy<=n&&mp[xx][yy]!='#'&&vis[xx][yy]==)
        return true;
    return false;
}
void dfs1(int xx,int yy,int step,int dir)//逆时针走法
{
    if(f==)
        return;
    if(xx==tail_x&&yy==tail_y)
    {
        f=;
        ans1=step;
        return;
    }
    if(dir==)//右上左下
    {
        if(judge(xx+,yy)) dfs1(xx+,yy,step+,);
        if(judge(xx,yy-)) dfs1(xx,yy-,step+,);
        if(judge(xx-,yy)) dfs1(xx-,yy,step+,);
        if(judge(xx,yy+)) dfs1(xx,yy+,step+,);
    }
    else if(dir==)//上左下右
    {
        if(judge(xx,yy-)) dfs1(xx,yy-,step+,);
        if(judge(xx-,yy)) dfs1(xx-,yy,step+,);
        if(judge(xx,yy+)) dfs1(xx,yy+,step+,);
        if(judge(xx+,yy)) dfs1(xx+,yy,step+,);
    }
    else if(dir==)//左下右上
    {

        if(judge(xx-,yy)) dfs1(xx-,yy,step+,);
        if(judge(xx,yy+)) dfs1(xx,yy+,step+,);
        if(judge(xx+,yy)) dfs1(xx+,yy,step+,);
        if(judge(xx,yy-)) dfs1(xx,yy-,step+,);
    }
    else//右下上左
    {
        if(judge(xx,yy+)) dfs1(xx,yy+,step+,);
        if(judge(xx+,yy)) dfs1(xx+,yy,step+,);
        if(judge(xx,yy-)) dfs1(xx,yy-,step+,);
        if(judge(xx-,yy)) dfs1(xx-,yy,step+,);
    }
}
void dfs2(int xx,int yy,int step,int dir)
{
    if(f==)
    {
        return;
    }
    if(xx==tail_x&&yy==tail_y)
    {
        f=;
        ans2=step;
        return;
    }
    if(dir==)
    {
        if(judge(xx-,yy)) dfs2(xx-,yy,step+,);
        if(judge(xx,yy-)) dfs2(xx,yy-,step+,);
        if(judge(xx+,yy)) dfs2(xx+,yy,step+,);
        if(judge(xx,yy+)) dfs2(xx,yy+,step+,);
    }
    else if(dir==)
    {
        if(judge(xx,yy+)) dfs2(xx,yy+,step+,);
        if(judge(xx-,yy)) dfs2(xx-,yy,step+,);
        if(judge(xx,yy-)) dfs2(xx,yy-,step+,);
        if(judge(xx+,yy)) dfs2(xx+,yy,step+,);

    }
    else if(dir==)
    {
        if(judge(xx+,yy)) dfs2(xx+,yy,step+,);
        if(judge(xx,yy+)) dfs2(xx,yy+,step+,);
        if(judge(xx-,yy)) dfs2(xx-,yy,step+,);
        if(judge(xx,yy-)) dfs2(xx,yy-,step+,);
    }
    else
    {
        if(judge(xx,yy-)) dfs2(xx,yy-,step+,);
        if(judge(xx+,yy)) dfs2(xx+,yy,step+,);
        if(judge(xx,yy+)) dfs2(xx,yy+,step+,);
        if(judge(xx-,yy)) dfs2(xx-,yy,step+,);
    }
}
int bfs()
{
    queue<node> q;
    while(!q.empty())
    {
        q.pop();
    }
    head.x=head_x,head.y=head_y,head.step=;
    q.push(head);
    vis[head_x][head_y]=;
    while(!q.empty())
    {
        head=q.front();
        q.pop();
        if(head.x==tail_x&&head.y==tail_y)
        {
            return head.step;
        }
        for(int i=; i<; i++)
        {
            tail.x=head.x+dir1[i][];
            tail.y=head.y+dir1[i][];
            if(judge(tail.x,tail.y))
            {
                tail.step=head.step+;
                vis[tail.x][tail.y]=;
                q.push(tail);
            }
        }
    }
    return ;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        memset(vis,,sizeof vis);
        scanf("%d%d",&n,&m);
        for(int i=; i<=m; i++)
        {
            for(int j=; j<=n; j++)
            {
                scanf(" %c",&mp[i][j]);
                if(mp[i][j]=='S')
                {
                    head_x=i;
                    head_y=j;
                }
                if(mp[i][j]=='E')
                {
                    tail_x=i;
                    tail_y=j;
                }
            }
        }
        f=;
        ans1=;
        dfs1(head_x,head_y,,);
        f=;
        ans2=;
        dfs2(head_x,head_y,,);
        int ans3=bfs();
        printf("%d %d %d\n",ans1,ans2,ans3);
    }
}

棋盘问题

n表示棋盘的大小是n*n，m表示棋子的数量，结束dfs的条件就是当前的棋子数量大于等于m(因为初始的0就已经存在1颗棋子了)。

#include<iostream>
#include<algorithm>
#include<string>
#include<string.h>
#define IO ios::sync_with_stdio(false), cin.tie(0)
typedef long long ll;
using namespace std;
const ll maxn=1e5+;
char mp[][];
bool vis[];
ll n,m,s;
void dfs(ll x,ll y)
{
    if(y>=m)
    {
        s++;
        return;
    }
    for(ll i=x; i<n; i++)
        for(ll j=; j<n; j++)
        {
            if(vis[j]==false&&mp[i][j]=='#')
            {
                vis[j]=true;
                dfs(i+,y+);
                vis[j]=false;
            }
        }
}
int main()
{
    while()
    {
        scanf("%lld%lld",&n,&m);
        if(n==-&&m==-)
            break;
        memset(vis,,sizeof vis);
        memset(mp,,sizeof mp);
        for(ll i=; i<n; i++)scanf("%s",mp[i]);
        s=;
        dfs(,);
        cout<<s<<endl;
    }
}

Oil Deposit

#include <bits/stdc++.h>
using namespace std ;
typedef long long ll;
ll m,n;
char mp[][];
ll dir[][]= { {,},{-,},{-,},{-,-},{,-},{,-},{,},{,} };//方向可以任意，当前方向见图
void dfs(ll x,ll y)
{
    mp[x][y]='*';//把当前的@转换成*，避免重复查找
    for(ll i=; i<; i++)
    {
        ll xx=x+dir[i][],yy=y+dir[i][];
        if(xx>=&&xx<=m&&yy>=&&yy<=n&&mp[xx][yy]=='@')
        {
            dfs(xx,yy);
        }
    }
    return;//递归结束
}
int main()
{
    while(~scanf("%lld%lld",&m,&n)&&n&&m)
    {
        ll sum=;
        for(ll i=; i<=m; i++)
        {
            for(ll j=;j<=n;j++)
            {
                cin>>mp[i][j];
                //scanf(" %c",&mp[i][j]);
                //两种读入方式均可，要注意的是，用scanf()读入的话，需要在%c之前加入一个空格，这是专门用来吸收"\n"
            }
        }
        for(ll i=; i<=m; i++)
        {
            for(ll j=; j<=n; j++)
            {
                if(mp[i][j]=='@')
                {
                    dfs(i,j);
                    sum++;
                }
            }
        }
        cout<<sum<<endl;
    }
}

Red and Black

用dfs搜索最长路，黑砖可走，红砖不可走，@表示出发点，输出最大黑砖数

#include<iostream>
#include<string>
#include<cstdio>
using namespace std;
typedef long long ll;
ll m,n;
char mp[][];
ll dir[][]={ {-,},{,},{,-},{,} };
ll s;
void dfs(ll x,ll y)
{
    ll xx,yy;
    for(ll i=;i<;i++)
    {
        xx=x+dir[i][];
        yy=y+dir[i][];
        if(xx>=&&xx<=n&&yy>=&&yy<=m&&mp[xx][yy]!='#')
        {
            s++;
            mp[xx][yy]='#';
            dfs(xx,yy);
        }
    }
}
int main()
{
    while(~scanf("%lld %lld",&m,&n)&&m&&n)
    {
        ll xx,yy;
        for(ll i=;i<=n;i++)
        {
            for(ll j=;j<=m;j++)
            {
                scanf(" %c",&mp[i][j]);
                if(mp[i][j]=='@')
                {
                    xx=i;
                    yy=j;
                }
            }
        }
        s=;
        mp[xx][yy]='#';
        dfs(xx,yy);
        cout<<s<<endl;
    }
}

P1162 填涂颜色

建议从1开始读入，因为这样有一个好处，能够建立起天然的下标为0的围墙数组，可以防止数组下标小于0，以至于越界

dfs1

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll maxn=1e6+;
ll n;
ll mp[][];
ll vis[][];
ll dir[][]= { {-,},{,},{,-},{,} };
void dfs(ll x,ll y)
{
    if(x==||y==||x>n||y>n)
        return;
    for(ll i=; i<; i++)
    {
        ll xx=x+dir[i][],yy=y+dir[i][];
        if(mp[xx][yy]!=&&xx>=&&xx<=n&&yy>=&&yy<=n&&!vis[xx][yy])
        {
            vis[xx][yy]=;
            dfs(xx,yy);
        }
    }
}
int main()
{
    memset(vis,,sizeof vis);
    memset(mp,,sizeof mp);
    scanf("%lld",&n);
    for(ll i=; i<=n; i++)
    {
        for(ll j=; j<=n; j++)
        {
            cin>>mp[i][j];
        }
    }
    for(ll i=;i<=n;i++)
    {
        if(mp[][i]==)
            dfs(,i);
        if(mp[i][]==)
            dfs(i,);
        if(mp[n][i]==)
            dfs(n,i);
        if(mp[i][n]==)
            dfs(i,n);
    }
    for(ll i=; i<=n; i++)
    {
        for(ll j=; j<=n; j++)
        {
            if(j>)
                cout<<' ';
            if(mp[i][j]!=&&!vis[i][j])
                mp[i][j]=;
                cout<<mp[i][j];
        }
        cout<<endl;
    }
}

dfs2

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll mp[][];
ll n;
ll dir[][]={ {-,},{,},{,-},{,} };
void dfs(ll x,ll y)
{
    mp[x][y]=;
    for(ll i=;i<;i++)
    {
        ll xx=x+dir[i][],yy=y+dir[i][];
        if(xx>=&&yy>=&&xx<=n+&&yy<=n+&&mp[xx][yy]==)
        {
            dfs(xx,yy);
        }
    }
}
int main()
{
    scanf("%lld",&n);
    for(ll i=;i<=n;i++)
    {
        for(ll j=;j<=n;j++)
        {
            cin>>mp[i][j];
        }
    }
    dfs(,);
    for(ll i=;i<=n;i++)
    {
        for(ll j=;j<=n;j++)
        {
            if(j>)
            {
                cout<<' ';
            }
            if(mp[i][j]==)
            {
                mp[i][j]=;
            }
            else if(mp[i][j]==)
            {
                mp[i][j]=;
            }
            cout<<mp[i][j];
        }
        cout<<endl;
    }
}

-------------------------------------------------------------------------------------------------------------