六、C++离散傅里叶逆变换

C++离散傅里叶逆变换

一、序言：

该教程承接上文的离散傅里叶变换，用于进行离散傅里叶逆变换。

二、设计目标

对复数数组进行离散傅里叶逆变换，并生成可供使用的图像类。

三、详细步骤

输入：经傅里叶变换后产生的复数数组

输出：MyImage图像

定义：

static MyImage* Idft2(ComplexNumber *Scr,int const width,int const height);

实现：MyImage* MyCV::Idft2(ComplexNumber *Scr, int width, int height)

{

    int bytesPerLine = (width*+)/*;

    double* double_data = new double[width*height];

    memset(double_data,,sizeof(double_data)*sizeof(double)); //全部赋值为0

    double fixed_factor_for_axisX = ( * PI) / height;                  // evaluate i2π/N of i2πux/N, and store the value for computing efficiency

    double fixed_factor_for_axisY = ( * PI) / width;                   // evaluate i2π/N of i2πux/N, and store the value for computing efficiency

    for (int x = ; x<height; x++) {

        for (int y = ; y<width; y++) {

            for (int u = ; u<height; u++) {

                for (int v = ; v<width; v++) {

                    double powerU = u * x * fixed_factor_for_axisX;         // evaluate i2πux/N

                    double powerV = v * y * fixed_factor_for_axisY;         // evaluate i2πux/N

                    ComplexNumber cplTemp;

                    cplTemp.SetValue(cos(powerU + powerV), sin(powerU + powerV));

                    double_data[y + x*width] = double_data[y + x*width] +

                            ((Scr[v + u*width] * cplTemp).m_rl

                            /(height*width));

                }

            }

        }

    }

    unsigned char *idft2_data = new unsigned char[bytesPerLine*height];//存储处理后的数据

    for(int i=;i<height;i++)

        for(int j=;j<width;j++)

        {

            idft2_data[i*bytesPerLine+j] = (unsigned char)double_data[i*width+j];

        }

    return new MyImage(idft2_data,width,height,MyImage::format::GRAY8);

}

至此，离散傅里叶逆变换的方法实现完成，效果图如下：

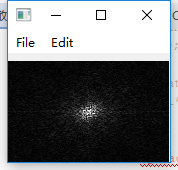
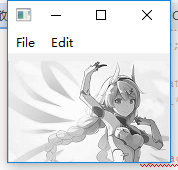
如果上述教程或代码中有任何错误，欢迎批评和指证。