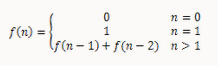剑指Offer面试题:8.斐波那契数列
一、题目:斐波那契数列
题目:写一个函数,输入n,求斐波那契(Fibonacci)数列的第n项。斐波那契数列的定义如下:
二、效率很低的解法
很多C/C++/C#/Java语言教科书在讲述递归函数的时候,大多都会用Fibonacci作为例子,因此我们会对这种解法烂熟于心:
public static long FibonacciRecursively(uint n)
{
if (n <= )
{
return ;
}
if (n == )
{
return ;
} return FibonacciRecursively(n - ) + FibonacciRecursively(n - );
}
上述递归的解法有很严重的效率问题,通过求解第10项的调用过程图来分析:
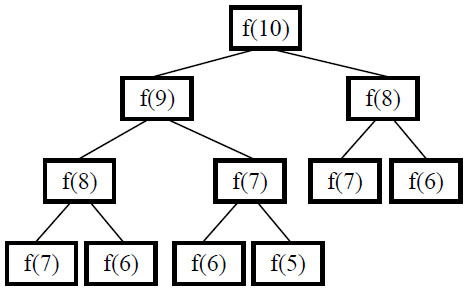
从上图中不难发现:在这棵树中有很多结点是重复的,而且重复的结点数会随着n的增大而急剧增加,这意味计算量会随着n的增大而急剧增大。事实上,用递归方法计算的时间复杂度是以n的指数的方式递增的。
三、实用循环的解法
改进的方法并不复杂。上述递归代码之所以慢是因为重复的计算太多,我们只要想办法避免重复计算就行了。这里的办法是从下往上计算,首先根据f(0)和f(1)算出f(2),再根据f(1)和f(2)算出f(3)……依此类推就可以算出第n项了。很容易理解,这种思路的时间复杂度是O(n)。
public static long FibonacciIteratively(uint n)
{
int[] result = { , };
if (n < )
{
return result[n];
} long fibNMinusOne = ;
long fibNMinusTwo = ;
long fibN = ; for (uint i = ; i <= n; i++)
{
fibN = fibNMinusOne + fibNMinusTwo; fibNMinusTwo = fibNMinusOne;
fibNMinusOne = fibN;
} return fibN;
}
四、单元测试
(1)单元测试用例
[TestMethod]
public void FibonacciTest1()
{
Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(),);
} [TestMethod]
public void FibonacciTest2()
{
Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(), );
} [TestMethod]
public void FibonacciTest3()
{
Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(), );
} [TestMethod]
public void FibonacciTest4()
{
Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(), );
} [TestMethod]
public void FibonacciTest5()
{
Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(), );
} [TestMethod]
public void FibonacciTest6()
{
Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(), );
} [TestMethod]
public void FibonacciTest7()
{
Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(), );
} [TestMethod]
public void FibonacciTest8()
{
Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(), );
} [TestMethod]
public void FibonacciTest9()
{
Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(), );
} [TestMethod]
public void FibonacciTest10()
{
Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(), );
} [TestMethod]
public void FibonacciTest11()
{
Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(), );
} [TestMethod]
public void FibonacciTest12()
{
Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(), );
}
(2)单元测试结果
①测试通过结果
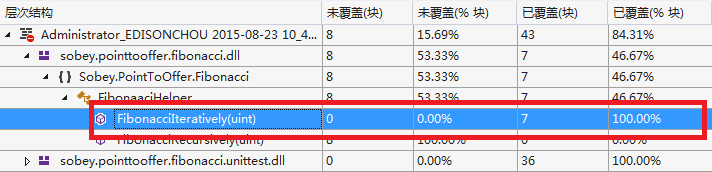
②代码覆盖率
剑指Offer面试题:8.斐波那契数列的更多相关文章
- 剑指Offer - 九度1387 - 斐波那契数列
剑指Offer - 九度1387 - 斐波那契数列2013-11-24 03:08 题目描述: 大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项.斐波那契数列的定义如下: ...
- 剑指offer第二版-10.斐波那契数列
面试题10:斐波那契数列 题目要求: 求斐波那契数列的第n项的值.f(0)=0, f(1)=1, f(n)=f(n-1)+f(n-2) n>1 思路:使用循环从下往上计算数列. 考点:考察对递归 ...
- 【剑指offer】9、斐波拉契数列
面试题9.斐波拉契数列 题目: 输入整数n,求斐波拉契数列第n个数. 思路: 一.递归式算法: 利用f(n) = f(n-1) + f(n-2)的特性来进行递归,代码如下: 代码: long long ...
- 剑指offer【07】- 斐波那契数列(java)
题目:斐波那契数列 考点:递归和循环 题目描述:大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0),n<=39. 法一:递归法,不过递归比较慢, ...
- 剑指offer(7)斐波那契数列
题目描述 大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项. n<=39 题目分析 我们都知道斐波那契可以用递归,但是递归重复计算的部分太多了(虽然可以通过),但是这 ...
- 【剑指Offer】7、斐波那契数列
题目描述: 大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0).假设n<=39. 解题思路: 斐波那契数列:0,1,1,2,3, ...
- 【剑指offer】7:斐波那契数列
题目描述: 大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0,第1项是1).假设 n≤39 解题思路: 斐波拉契数列:1,1,2,3,5,8--,总结 ...
- 剑指offer——矩阵覆盖(斐波那契变形)
****感觉都可以针对斐波那契写一个变形题目的集合了****** 我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形.请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法? cl ...
- 【剑指offer】面试题 10. 斐波那契数列
面试题 10. 斐波那契数列 题目一:求斐波那契数列的第n项 题目描述:求斐波拉契数列的第n项 写出一个函数,输入n,求斐波拉契(Fibonacci)数列的第n项.斐波拉契数列定义如下: C++ 实现 ...
- 剑指offer编程题Java实现——面试题9斐波那契数列
题目:写一个函数,输入n,求斐波那契数列的第n项. package Solution; /** * 剑指offer面试题9:斐波那契数列 * 题目:写一个函数,输入n,求斐波那契数列的第n项. * 0 ...
随机推荐
- 【Java EE 学习 83 上】【SpringMVC】【基本使用方法】
一.SpringMVC框架概述 什么是SpringMVC?SpringMVC是一个和Struts2差不多的东西,他们的作用和性质几乎是相同的,甚至开发效率上也差不多,但是在运行效率上SpringMVC ...
- [译]:Xamarin.Android平台功能——位置服务
返回索引目录 原文链接:Location Services. 译文链接:Xamarin.Android平台功能--位置服务 本部分介绍位置服务以及与如何使用位置提供商服务 Location Servi ...
- vue-loader配合webpack的使用及安装
vue-loader配合webpack的使用及安装: 工程文件简单的目录结构 index.html main.js 入口文件 App.vue vue文件,官方推荐命名法 package.jso ...
- “玲珑杯”ACM比赛 Round #7 B -- Capture(并查集+优先队列)
题意:初始时有个首都1,有n个操作 +V表示有一个新的城市连接到了V号城市 -V表示V号城市断开了连接,同时V的子城市也会断开连接 每次输出在每次操作后到首都1距离最远的城市编号,多个距离相同输出编号 ...
- Python 判断变量的类型
这里有两种方法.type 和isinstance import types aaa = 0 print type(aaa) if type(aaa) is types.IntType: print & ...
- Java EE之servlet处理表单提交的请求
1.在源包下新建一个Servlet页,取名为LoginServlet: package weinidingServlet; //该Servlet所 ...
- [spring源码学习]三、IOC源码——自定义配置文件读取
一.环境准备 在文件读取的时候,第9步我们发现spring会根据标签的namespace来选择读取方式,联想spring里提供的各种标签,比如<aop:xxx>等应该会有不同的读取和解析方 ...
- 二分+DP+Trie HDOJ 5715 XOR 游戏
题目链接 XOR 游戏 Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)Total ...
- 整理 PHPstorm实用个人配置,修改调整个性化快捷键,修改使用phpstorm创建的模板的默认注释:
对你有助请点赞,请顶------送人玫瑰,手留余香! 1:58 2016/3/12 整理PHPstorm实用个人配置,修改调整个性化快捷键,修改使用phpstorm创建的模板的默认注释: PHPsto ...
- 【专业找水题】状压dp最水题,没有之一
题目链接 现在代码能力没上升,倒是越来越会找水题了(比例题还水的裸题你值得拥有) 这网站不是针对竞赛的,所以时空限制都很宽松 然后就让我水过去了 对于每个点,包括自己的前m个元素是否取都是一种状态,所 ...