【算法总结】Manacher's Algorithm

　　Manacher's Algorithm针对的是最长回文子串问题。对于此问题，最直接的方法是遍历每一个元素，遍历过程中以每一个字符为中心向两边扩展以寻找此字符为中心的最长回文子串。复杂度O(n²)。Manacher算法将时间复杂度降至O(n)，关键点在于将奇偶字串统一成奇数字串。

　　方法是在每一个字符的左右都加上一个特殊字符，如'#'

　　”abccba" -> "#a#b#c#c#b#a#"

　　"abcba"  -> "#a#b#c#b#a#"

　　对于长度为n的字符串，需添加 n+1 个特殊字符，则新字符串长度为 2n+1。从而解决了奇偶字串分情况判断问题。

　　假设原字符串为 str，添加特殊字符串后的新字符串为 trans，设立长度与 trans 相同的一个数组 p，p[i] 代表以 trans[i] 为中心的最长回文字串的半径，例如对于trans = "#a#b#c#"， p[2] = 2（”#a#“）, p[3] = 1（”#“）。　　

　　trans ：# 1 # 2 # 2 # 1 # 2 # 2 #
　　p       ：1 2 1 2 5 2 1 6 1 2 3 2 1

　　p 数组的一个性质是 p[i] - 1 即是以 trans[i]（trans[i] 为原字符串中元素） 为中心的最长回文字串在原字符串S中的长度。证明：首先在转换得到的字符串 trans 中，所有的回文字串的长度都为奇数，那么对于以 trans[i] 为中心的最长回文字串，其长度就为 2*p[i]-1 ,经过观察可知，trans 中所有的回文子串，其中分隔符的数量一定比其他字符的数量多1，也就是有 p[i] 个分隔符，剩下 p[i]-1 个字符来自原字符串，所以该回文串在原字符串中的长度就为 p[i]-1。

　　因为添加的特殊字符也需要搜索其最长回文字串，那么为了避免复杂的边界讨论，需要在字符串首尾各添加与之前添加的特殊字符不同的另一特殊字符作为边界。(通常只在首部添加，尾部不需要添加的原因是字符串的结尾为 '\0' ,相当于已经加过了。所以如果在某种情况下字符串没有默认的 '\0'结尾，那么需要人为的添加一个特殊字符)

　　添加两个辅助变量，mx 和 id。mx是目前最长回文字串能延伸的最右位置。id 为 最长回文字串的对称轴所在位置。

　　1. 当 mx > i

　　　最长回文字串为 (trans[2 * id - mx], trans[mx]).  i 在此最大回文字串中，j 为 i 关于 id 的对称点

　　　　1) mx - i > p[j]

　                  　

　　　　

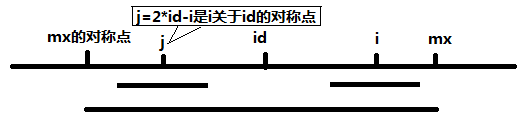
　　　　　　　　当 mx - i > p[j]，说明 p[i] = p[j] = p[2*id - i]。因为 j 是 i 关于 id 的对称点，既然 以 j 为中心的最长回文字串都在 以 id 为中心的回文字串中，那么 以 i 为中心的回文字串也应该在以 id 为中心的回文字串中。假设 以 j 为中心的最长回文字串左端点为 begin，右端点为 end，那么由于 mx - i > p[j]，所以 j - mx > p[j]， 所以 begin > mx的对称点，end < id。相同的，由于以 i 为中心的回文字串也应该在 （id，mx）范围内，因为 i 和 j 都在回文串(mx对称点， mx）内，那么（mx， j）与（i，mx）相同。所以 p[i] = p[j]

　　　　2) mx - i <= p[j]

　　　　　　

　　　　　　　　当 mx - i <= p[j] 时，以 j 为中心的回文子串不一定完全包含于以 id 为中心的回文子串中，但是基于对称性可知，图中两个绿框所包围的部分是相同的，也就是说以i 为中心的回文子串，其向右至少会扩展到 mx 的位置，也就是说 P[i] >= mx - i。至于 mx 之后的部分是否对称，只能通过遍历得知了。

　　2. 当 mx <= i

　　　　说明以 i 为对称轴的回文串还没有任何一个部分被访问过，于是只能从 i 的左右两边开始尝试扩展了，当左右两边字符不同，或者到达字符串边界时停止。然后更新 mx 和 id 。

　　最长回文子串对应原串中的位置：l = (i - p[i])/2; r = (i + p[i])/2 - 2;

　　

 #include <iostream>
 #include <string.h>
 #include <stdio.h>

 using namespace std;
 const int N=<<;

 char T[N];   //原字符串
 char S[N];   //转换后的字符串
 int  R[N];   //回文半径

 void Init(char *T)
 {
     S[] = '$';
     int len = strlen(T);
     for(int i = ; i <= len; i++)
     {
         S[*i + ] = '#';
         S[*i + ] = T[i];
     }
 }

 void Manacher(char *S)
 {
     int k = ,mx = ;
     int len = strlen(S);
     for(int i = 1; i < len; i++)
     {
         if(mx > i)
             R[i] = R[*k - i] < mx - i? R[*k-i] : mx-i;
         else
             R[i] = ;
         while(S[i + R[i]] == S[i - R[i]])
             R[i]++;
         if(R[i] + i > mx)
         {
             mx = R[i] + i;
             k = i;
         }
     }
 }

 int main()
 {
     while(~scanf("%s", T))
     {
         Init(T);
         Manacher(S);
         int len = strlen(S);
         int ans = ;
         for(int i = ; i<len; i++)
             ans = R[i] > ans? R[i] : ans;
         printf("%d\n", ans - );
     }
     return ;
 } 

转自：链接 ，链接

　注意：题目中的S[i + R[i]] == S[i - R[i]]实际上已经属于越界访问，但由于语言和编译器的不同，对于越界问题处理也不同。