雅礼集训 2017 Day2 水箱可并堆

题目描述

给出一个长度为 n 宽度为 1 ，高度无限的水箱，有 n−1 个挡板将其分为 n 个 1 - 1 的小格，然后向每个小格中注水，水如果超过挡板就会溢出到挡板的另一边，这里的水是满足物理定律的（在无挡板阻拦的情况下会向低处流），现在有 m 个条件 (i,y,k) ，表示从左到右数的第 i 个格子中，在高度为 y+0.5 的地方是否有水，k=1 表示有水，k=0 表示没有水，请求出这 m 个条件最多能同时满足多少个条件。本题有多组数据。

输入格式

第一行一个正整数 T ，为数据组数。
第二行两个正整数 n 、m ，中间用空格隔开。
接下来一行 n−1 个整数，表示从左到右每一块隔板的高度。
接下来 m 行，每行三个整数 i 、y 、k ，表示一个条件。

输出格式

共 T 行，每行对应一组数据的答案。

样例

样例输入

样例输出

3

1

数据范围与提示

对于 20% 的数据，n,m≤16；
对于另外 10% 的数据，只存在指明某处有水的条件；
对于另外 30% 的数据，n,m≤1000；
对于 100% 的数据，n,m≤1e5,T≤5；

看到这道题，首先应该想到最高的隔板把整个区间分割成两个独立的部分，所以对于整段的答案，可以是左右两个部分的独立的答案(即水没有淹没最高的那个隔板），或者先把两个部分淹没，让水没过最高的隔板，然后在两侧最近的更高的隔板(箱壁可视为无限高的隔板)的高度以下讨论答案。

我用的是线段树维护区间最高挡板位置，用可并堆维护区间所有要求。

初始时，对于每一个单位水槽，把它上方所有要求按高度维护小根堆，合并时就先直接合并它左右两个部分，再将堆中左右小于两侧隔板高度的要求按照顺序提出来，枚举淹没高度，用前缀有水条件个数加后缀无水条件个数更新答案，设这个答案最大值为sum。

对于区间[L,R],若L=R，ans(L,R)=sum。

否则，[L,R]一定能从最高的隔板处分为[L,k]，[k+1,R]，两个部分，

可以用ans(L,k)+ans(k+1,R)+高于第k和第k+1之间的隔板低于L外侧隔板且低于R外侧隔板间所有无水条件的个数更新答案，

也可以用所有[L,R]之间低于第k和第k+1之间的隔板的有水条件个数+sum更新答案。

是的有点像分治...

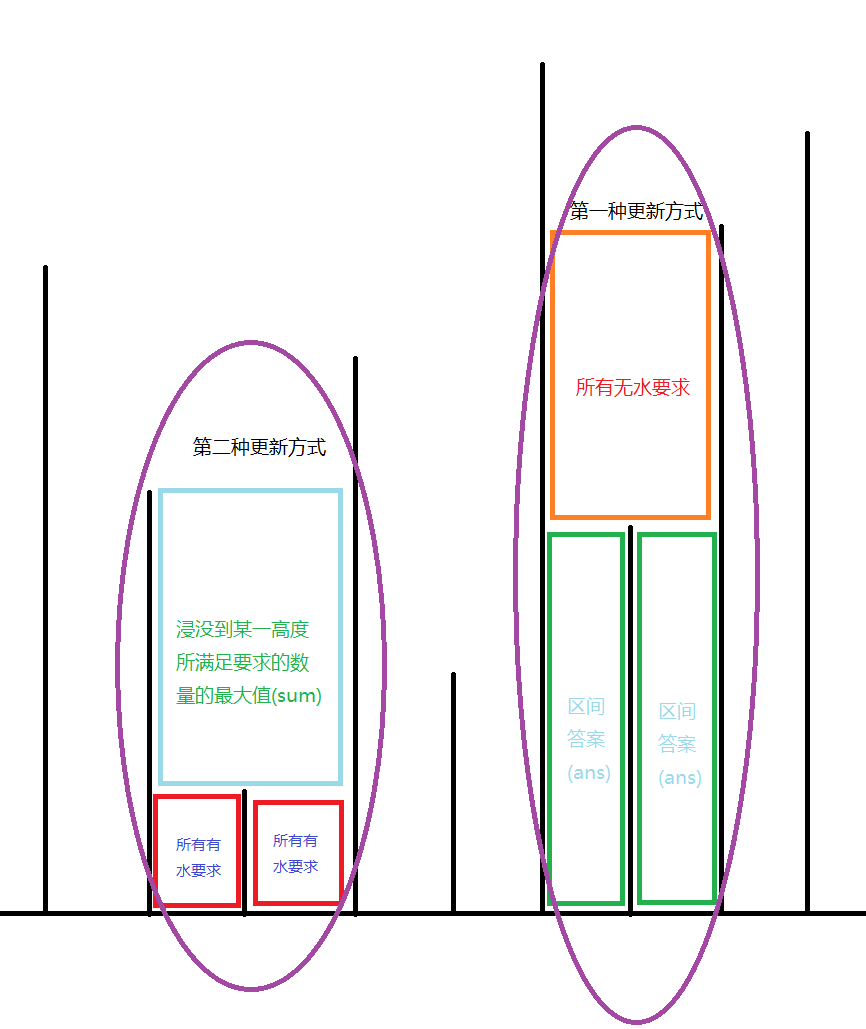
复杂度分析的话，每个隔板可以和左侧比它高的第一个隔板和右侧比它高的第一个隔板分别形成两个区间，所以大概有2n个区间吧...然后每个要求在可并堆中共计被访问一次，删除一次，所以再加一个mlogm，肯定是能过的。

AC代码如下:

#include<algorithm>

#include<iostream>

#include<cstring>

#include<cstdio>

#include<cmath>

#define LL long long

#define M 200020

#define mid (l+r>>1)

using namespace std;

int read(){

	int nm=0,fh=1;char cw=getchar();

	for(;!isdigit(cw);cw=getchar()) if(cw=='-') fh=-fh;

	for(;isdigit(cw);cw=getchar()) nm=nm*10+(cw-'0');

	return nm*fh;

}

struct req{int pos,hs,tpe;}p[M];

bool cmp(req i,req j){

	if(i.pos==j.pos) return i.hs<j.hs;

	return i.pos<j.pos;

}

int n,m,T,tmp,L[M],R[M],c[M<<2],t[M],ans,rt[M<<2],f[M<<2];

int tot[M<<2],dst[M<<2],son[M][2],fs[M],gt[M],pre[M],suf[M],tk;

void build(int x,int l,int r){

	if(l==r){c[x]=l;return;}

	build(x<<1,l,mid),build(x<<1|1,mid+1,r);

	if(t[c[x<<1]]>t[c[x<<1|1]]) c[x]=c[x<<1];

	else c[x]=c[x<<1|1];

}

int top(int x,int l,int r,int lt,int rt){

	if(rt<l||r<lt) return lt;

	if(lt<=l&&r<=rt) return c[x];

	int t1=top(x<<1,l,mid,lt,rt),t2=top(x<<1|1,mid+1,r,lt,rt);

	return t[t1]>t[t2]?t1:t2;

}

int merge(int x,int y){

	if(x*y==0) return x+y;

	if(p[x].hs>p[y].hs) return merge(y,x);

	int t1=son[x][0],t2=son[x][1],k=merge(t2,y);

	son[x][1]=k;

	if(dst[k]>dst[t1]) swap(k,t1);

	dst[x]=dst[k]+1,son[x][0]=t1,son[x][1]=k;

	return x;

}

int del(int x){

	int t1=son[x][0],t2=son[x][1];

	son[x][0]=son[x][1]=dst[x]=0;

	return merge(t1,t2);

}

void dp(int &x,int l,int r){

	x=++tmp,f[x]=tot[x]=0;

	int cnt=0,rf=min(t[l-1],t[r]),sum=0;

	if(l==r) rt[x]=fs[l];

	else{

	    int tp=top(1,1,n-1,l,r-1);

	    dp(L[x],l,tp),dp(R[x],tp+1,r);

		rt[x]=merge(rt[L[x]],rt[R[x]]);

		tot[x]=tot[L[x]]+tot[R[x]];

	}

	while(rt[x]>0){

		if(p[rt[x]].hs>=rf) break;

		if(p[rt[x]].tpe==1) tot[x]++;

		gt[++cnt]=rt[x],rt[x]=del(rt[x]);

	}

	suf[cnt+1]=0,pre[0]=0;

	for(int i=1;i<=cnt;i++){

		pre[i]=pre[i-1],suf[cnt-i+1]=suf[cnt-i+2];

		if(p[gt[i]].tpe==1) pre[i]++;

		if(p[gt[cnt-i+1]].tpe==0) suf[cnt-i+1]++;

	}

	for(int i=0;i<=cnt;i++){

		if(p[gt[i]].hs==p[gt[i+1]].hs&&i!=0) continue;

		sum=max(sum,pre[i]+suf[i+1]);

	}

	if(l==r){f[x]=sum;return;}

	f[x]=max(f[L[x]]+f[R[x]]+suf[1],tot[L[x]]+tot[R[x]]+sum);

}

int main(){

	T=read();

	while(T--){

		n=read(),m=read(),tmp=ans=tk=0,t[0]=t[n]=2147483646;

		memset(fs,0,sizeof(fs));

		for(int i=1;i<n;i++) t[i]=read();

		for(int i=1;i<=m;i++) p[i].pos=read(),p[i].hs=read(),p[i].tpe=read();

		build(1,1,n-1),sort(p+1,p+m+1,cmp);

		for(int i=1;i<=m;i++){fs[p[i].pos]=merge(i,fs[p[i].pos]);}

		dp(tk,1,n),printf("%d\n",f[tk]);

	}

    return 0;

}