算法（Algorithms）第4版 练习 1.5.2

0 1 2 3 4 5 6 7 8 9
10 components
9 0
0 1 2 3 4 5 6 7 8
9 components
3 4
0 1 2  4 5 6 7 8 0
8 components
5 8
0 1 2 4 4  6 7 8 0
7 components
7 2
0 1 2 4 4 8 6  8 0
6 components
2 1
0 1  4 4 8 6 2 8 0
5 components
5 7
0 1 1 4 4 8 6 2  0
4 components
0 3
 1 1 4 4 8 6 2 1 0
3 components
4 2
4 1 1 4  8 6 2 1 0
2 components

森林图：

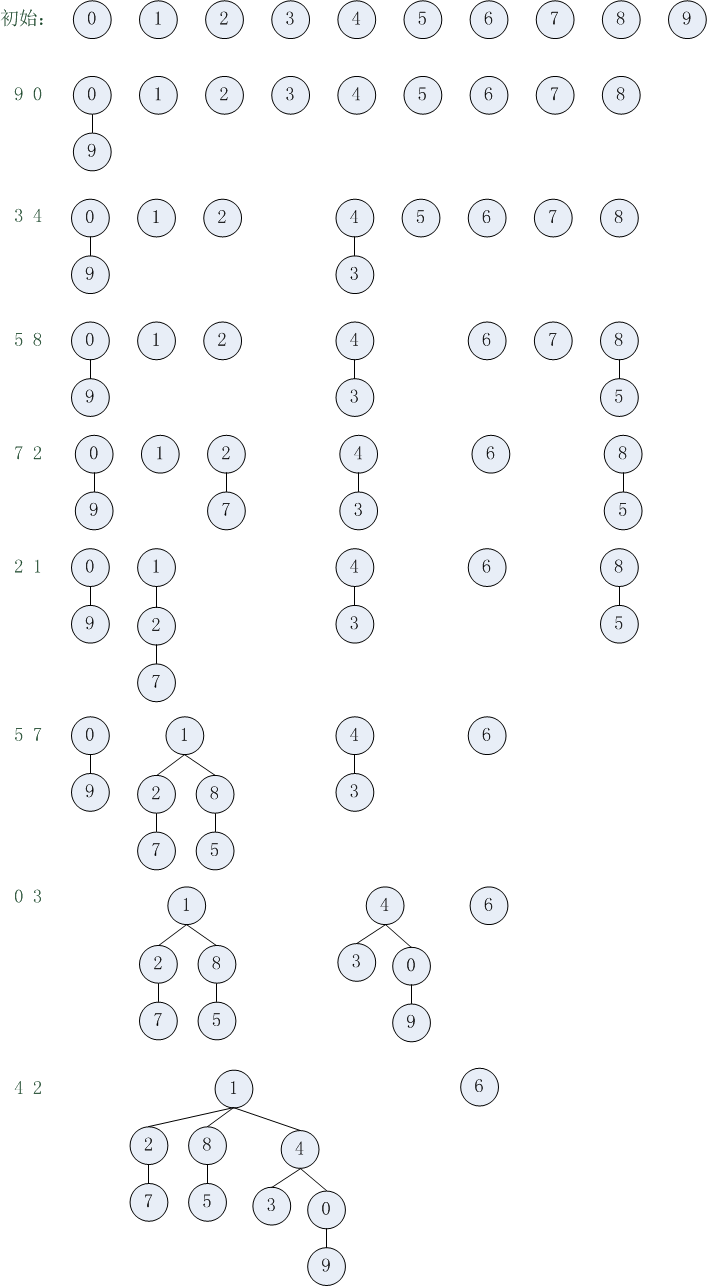
操作次数分析：

find函数每次访问数组次数是1 + 2 * depth

connected函数每次调用两次find函数

union函数每次调用两次find函数（如果两个连接点不在同一个树的话，则多一次数组访问）

　　public static void main(String[] args) {

        //initialize N components
        int N = StdIn.readInt();
        UFQuickUnion uf = new UFQuickUnion(N);
        StdOut.println(uf);

        while(!StdIn.isEmpty()) {

            int p = StdIn.readInt();
            int q = StdIn.readInt();

            if(uf.connected(p, q)) {//ignore if connected
                StdOut.println(p + " " + q + " is connected");
                continue;
            }

            uf.union(p, q);//connect p and q
            StdOut.println(p + " " + q);
            StdOut.println(uf);
        }

    }

对于这个client，对每个数据对，都调用一次connected函数和union函数。

下边对数组访问次数进行分析：

9 0：9和0的深度都为0，find访问数组次数为1，connected为2 * 1， union为2 * 1 + 1，总的为2 * 1　　+ 2 * 1 + 1

3 4：3和4的深度都为0，find访问数组次数为1，connected为2 * 1， union为2 * 1 + 1，总的为2 * 1　　+ 2 * 1 + 1

5 8：5和8的深度都为0，find访问数组次数为1，connected为2 * 1， union为2 * 1 + 1，总的为2 * 1　　+ 2 * 1 + 1

7 2：7和2的深度都为0，find访问数组次数为1，connected为2 * 1， union为2 * 1 + 1，总的为2 * 1　　+ 2 * 1 + 1

2 1：2和1的深度都为0，find访问数组次数为1，connected为2 * 1， union为2 * 1 + 1，总的为2 * 1　　+ 2 * 1 + 1

5 7：5的深度为1，7的深度为2。find访问数组次数分别为3、5，connected为3 + 5， union为3 + 5 + 1，总的为3 + 5　　+3 + 5 + 1

0 3：0的深度为0，3的深度为1。find访问数组次数分别为1、3，connected为1 + 3， union为1 + 3 + 1，总的为1 + 3　　+1 + 3 + 1

4 2：4的深度为0，2的深度为1。find访问数组次数分别为1、3，connected为1 + 3， union为1 + 3 + 1，总的为1 + 3　　+1 + 3 + 1

源代码：

package com.qiusongde;

import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;

public class UFQuickUnion {

    private int[] id;//save the site's parent link(site indexed)
    private int count;//number of components

    public UFQuickUnion(int n) {

        count = n;

        id = new int[n];
        for(int i = 0; i < n; i++)
            id[i] = i;

    }

    public int count() {
        return count;
    }

    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }

    public int find(int p) {

        //find root
        //id[p] save the parent of p
        while(p != id[p])
            p = id[p];

        return p;
    }

    public void union(int p, int q) {

        int pRoot = find(p);//find pRoot
        int qRoot = find(q);//find qRoot

        if(pRoot == qRoot)
            return;

        id[pRoot] = qRoot;
        count--;
    }

    @Override
    public String toString() {
        String s = "";

        for(int i = 0; i < id.length; i++) {
            s += id[i] + " ";
        }
        s += "\n" + count + " components";

        return s;
    }

    public static void main(String[] args) {

        //initialize N components
        int N = StdIn.readInt();
        UFQuickUnion uf = new UFQuickUnion(N);
        StdOut.println(uf);

        while(!StdIn.isEmpty()) {

            int p = StdIn.readInt();
            int q = StdIn.readInt();

            if(uf.connected(p, q)) {//ignore if connected
                StdOut.println(p + " " + q + " is connected");
                continue;
            }

            uf.union(p, q);//connect p and q
            StdOut.println(p + " " + q);
            StdOut.println(uf);
        }

    }

}