机器学习-- Logistic回归 Logistic Regression

转载自：http://blog.csdn.net/linuxcumt/article/details/8572746

1.假设随Tumor Size变化，预测病人的肿瘤是恶性（malignant）还是良性（benign）的情况。

给出8个数据如下：

2.假设进行linear regression得到的hypothesis线性方程如上图中粉线所示，则可以确定一个threshold:0.5进行predict

y=1, if h(x)>=0.5

y=0, if  h(x)<0.5

即malignant=0.5的点投影下来，其右边的点预测y=1;左边预测y=0；则能够很好地进行分类。

那么，如果数据集是这样的呢？

这种情况下，假设linear regression预测为蓝线，那么由0.5的boundary得到的线性方程中，不能很好地进行分类（5，6个点均不能满足）。因为不满足

y=1, h(x)>0.5

y=0, h(x)<=0.5

============Hypothesis Representation==================

1.logistic regression model

注意：

========================Decision Boundary =================================

1.logistic regression model的深入解释

2.所谓Decision Boundary就是能够将所有数据点进行很好地分类的h(x)边界。

如下图所示，假设形如h(x)=g(θ0+θ1x1+θ2x2)的hypothesis参数θ=[-3,1,1]T,
则有

predict Y=1, if -3+x1+x2>=0

predict Y=0, if -3+x1+x2<0

刚好能够将图中所示数据集进行很好地分类

3.小问题，注意，所有逻辑回归都这么处理。参见（1.logistic regression model的深入解释）

4.除了线性boundary还有非线性decision boundaries，比如

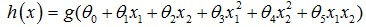。训练集的作用

就是找这些参数θ。但这个曲线该怎么找？？由此可见，logistic
regression 的

boundary可以是任意的曲线。而所谓的线性可分、不可分实则指的就是

boundary是否为线性或非线性（参数），而不是logistic函数自身。下图中，

进行分类的decision boundary就是一个半径为1的圆，如图所示：

======================Cost Function=====================

1.问题提出，如何求参数θ？但这个曲线该怎么找？？

2.对于logistic regression其COST函数不能像线性回归的最小二乘那样

选择。因为其 logistic是非线性函数。非要这样取的话，COST函数是非凸

函数，见下图。无法用梯度下降求极值。

3.logistic
regression其COST函数的定义。在给定了h(θ,x),y后，其COST函数

值即可确定。注意：h(θ,x)为logistic曲线，其取值范围在0-1之间。

4.当h(θ,x)接近1，而y=1,表明分类正确，故不“惩罚”，COST=0;

反之，h(θ,x)接近0，而y=1，,表明分类错误，故大大“惩罚”，COST=无限大;

同理对y=0

5.小题目

===========Simplified
Cost Function and Gradient Descent==============

1.求出最小J(θ)时的θ,然后计算h(θ,x)，若其>=0.5（或θTx>=0),则y=1;否则y=0.

参考logistic regression model

2.不管h(x)的表达式是线性的还是logistic
regression model, 都能得到如下的参数更新过程。

写的详细些：

3.归一化（Feature scaling)同样会使得logistic regression 跑的更快。

=============Advanced Optimization ==================

1.除了gradient descent 方法之外，我们还有很多方法可以使用，如下图所示，

左边是另外三种方法，右边是这三种方法共同的优缺点，无需选择学习率α，更快，

但是更复杂。

2.代码小例

3.实际matlab中已经帮我们实现好了一些优化参数θ的方法，那么这里我们需要完成的事情

只是写好cost function,并告诉系统，要用哪个方法进行最优化参数。比如我们用‘GradObj’

， Use the GradObj option to specify that FUN also returns a second output argument

G that is the partial derivatives of the function df/dX, at the point X.

函数costFunction, 定义jVal=J(θ)和对两个θ的gradient：

[plain] view
plaincopy

1. function [ jVal,gradient ] = costFunction( theta )
2. %COSTFUNCTION Summary of this function goes here
3. %   Detailed explanation goes here
4. jVal= (theta(1)-5)^2+(theta(2)-5)^2;
5. gradient = zeros(2,1);
6. %code to compute derivative to theta
7. gradient(1) = 2 * (theta(1)-5);
8. gradient(2) = 2 * (theta(2)-5);
9. end

编写函数Gradient_descent，进行参数优化

[plain] view
plaincopy

1. function [optTheta,functionVal,exitFlag]=Gradient_descent( )
2. %GRADIENT_DESCENT Summary of this function goes here
3. %   Detailed explanation goes here
4. options = optimset('GradObj','on','MaxIter',100);
5. initialTheta = zeros(2,1)
6. [optTheta,functionVal,exitFlag] = fminunc(@costFunction,initialTheta,options);
7. end

matlab主窗口中调用，得到优化厚的参数(θ1,θ2)=(5,5),即hθ(x)=θ1x1+θ2x2=5*x1+5*x2

[plain] view
plaincopy

1. [optTheta,functionVal,exitFlag] = Gradient_descent()
2. initialTheta =
3. 0
4. 0
5. Local minimum found.
6. Optimization completed because the size of the gradient is less than
7. the default value of the function tolerance.
8. <stopping criteria details>
9. optTheta =
10. 5
11. 5
12. functionVal =
13. 0
14. exitFlag =
15. 1

最后得到的结果显示出优化参数optTheta=[5,5], functionVal = costFunction(迭代后) = 0

===========Multiclass Classification: One-vs-all =================

1.所谓one-vs-all method就是将binary分类的方法应用到多类分类中。

比如我想分成K类，那么就将其中一类作为positive，另（k-1）合起来作为negative，

这样进行K个h(θ)的参数优化，每次得到的一个hθ(x)是指给定θ和x，它属于positive的

类的概率。按照上面这种方法，给定一个输入向量x，获得最大hθ(x)的类就是

x所分到的类。