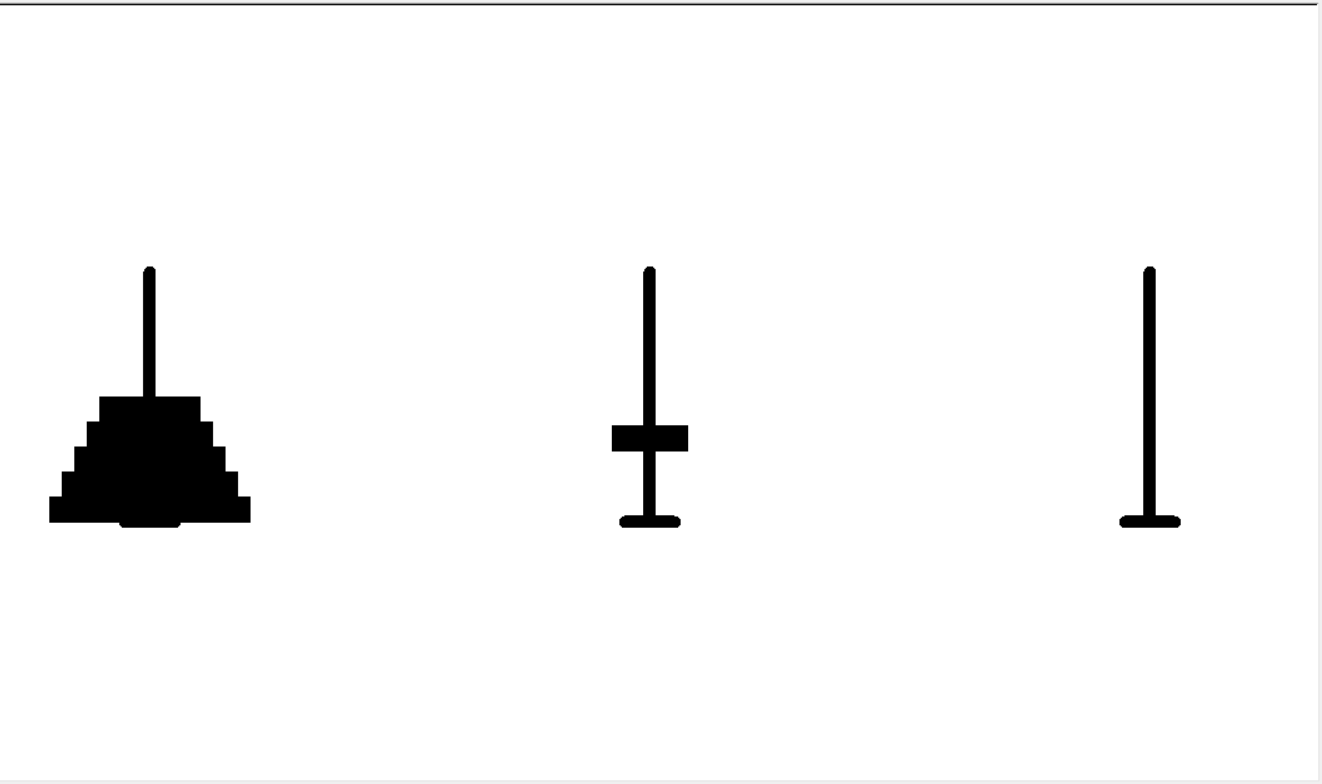turtle库实现汉诺塔
import turtle
turtle.screensize(800,800) class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return len(self.items) ==
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
if not self.isEmpty():
return self.items[len(self.items) - ]
def size(self):
return len(self.items) def drawpole_3():#画出汉诺塔的poles
t = turtle.Turtle()
t.hideturtle()
def drawpole_1(k):
t.up()
t.pensize()
t.speed()
t.goto(*(k-), )
t.down()
t.goto(*(k-), -)
t.goto(*(k-)-, -)
t.goto(*(k-)+, -)
drawpole_1()#画出汉诺塔的poles[0]
drawpole_1()#画出汉诺塔的poles[1]
drawpole_1()#画出汉诺塔的poles[2] def creat_plates(n):#制造n个盘子
plates=[turtle.Turtle() for i in range(n)]
for i in range(n):
plates[i].up()
plates[i].hideturtle()
plates[i].shape("square")
plates[i].shapesize(,-i)
plates[i].goto(-,-+*i)
plates[i].showturtle()
return plates def pole_stack():#制造poles的栈
poles=[Stack() for i in range()]
return poles def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
mov=poles[fp].peek()
plates[mov].goto((fp-)*,)
plates[mov].goto((tp-)*,)
l=poles[tp].size()#确定移动到底部的高度(恰好放在原来最上面的盘子上面)
plates[mov].goto((tp-)*,-+*l) def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
if height >= :
moveTower(plates,poles,height-,fromPole,withPole,toPole)
moveDisk(plates,poles,fromPole,toPole)
poles[toPole].push(poles[fromPole].pop())
moveTower(plates,poles,height-,withPole,toPole,fromPole) myscreen=turtle.Screen()
drawpole_3()
n=int(input("请输入汉诺塔的层数并回车:\n"))
plates=creat_plates(n)
poles=pole_stack()
for i in range(n):
poles[].push(i)
moveTower(plates,poles,n,,,)
myscreen.exitonclick() 执行完毕:
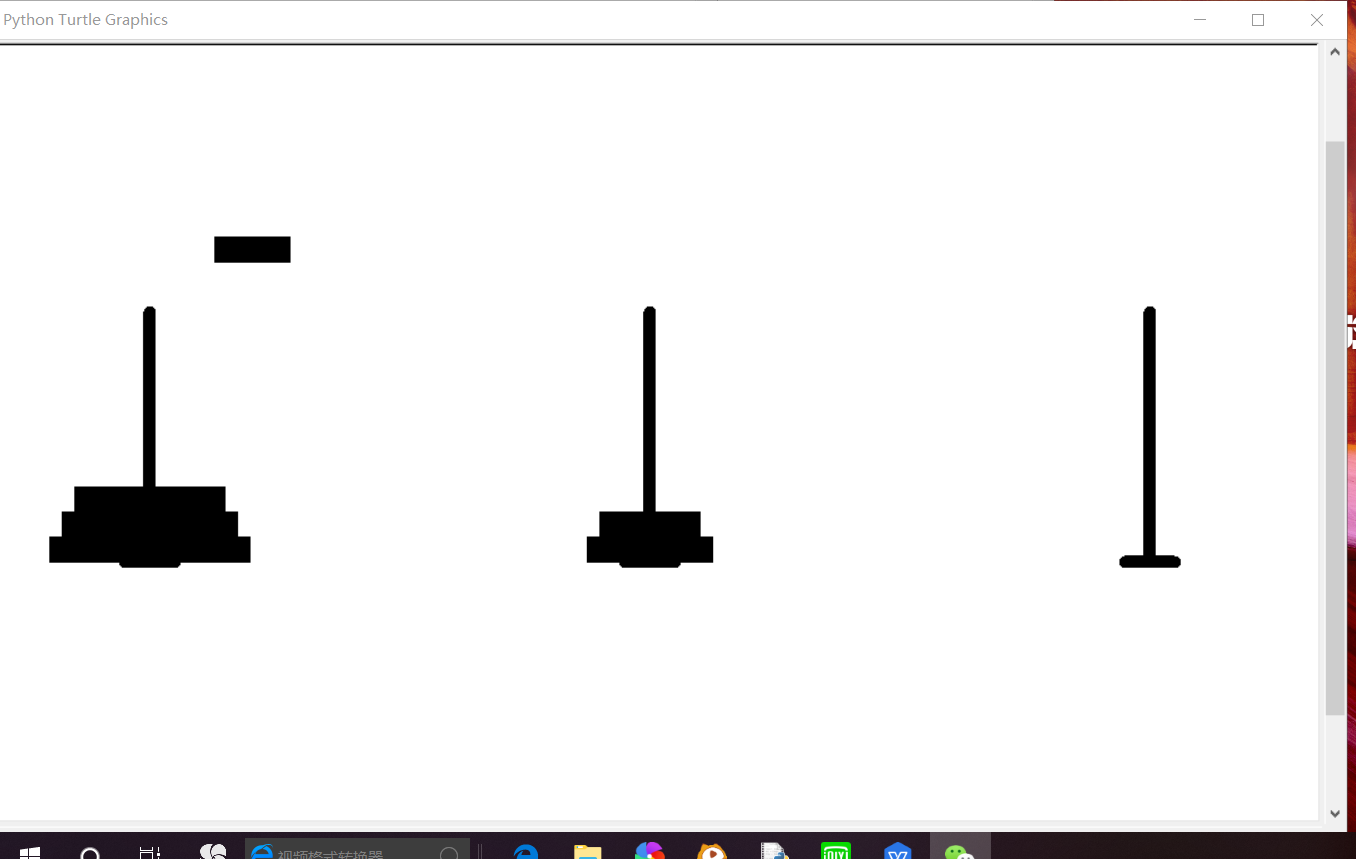
turtle库实现汉诺塔的更多相关文章
- 用turtle库实现汉诺塔问题~~~~~
汉诺塔问题 问题描述和背景: 汉诺塔是学习"递归"的经典入门案例,该案例来源于真实故事. ...
- 用turtle库显示汉诺塔问题的过程
用turtle库显示汉诺塔问题的过程 一.什么是汉诺塔问题? 一座汉诺塔,塔内有3个座A.B.C,A座上有n个盘子,盘子大小不等,大的在下,小的在上,如图所示.把这n个盘子从A座移到C座,但每次只能移 ...
- python运用turtle 画出汉诺塔搬运过程
python运用turtle 画出汉诺塔搬运过程 1.打开 IDLE 点击File-New File 新建立一个py文件 2.向py文件中输入如下代码 import turtle class Stac ...
- 用turtle实现动态汉诺塔
代码如下: (此代码最多可支持七层) import turtle class Stack: def __init__(self): self.items = [] def isEmpty(self): ...
- python中关于汉诺塔问题和使用turtle库实现其搬运过程
一.汉诺塔问题 汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘从下面开始按 ...
- Turtle库的建立——汉诺塔
Turtle库的建立——汉诺塔 1.首先是要用递归方法来完成这个汉诺塔法则 2.其次,就要编程好代码以及熟练掌握Turtle函数库 一. 相关代码如下: import turtle class St ...
- 运用Turtle实现汉诺塔的可视化运行(递归算法)
运用Turtle实现汉诺塔的可视化运行(递归算法) 汉诺塔问题又名河内塔问题,是源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆 ...
- 递归可视化之汉诺塔的动画实现(turtle海龟)
import turtle class Stack: def __init__(self): self.items = [] def isEmpty(self): def push(self, ite ...
- 用python turtle实现汉诺塔的移动
1.汉诺塔 汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘从下面开始按大小 ...
随机推荐
- jqGrid基本用法与示例
转自:https://chuanlu.iteye.com/blog/1953544 一.jqGrid的基本用法 1.html页面 <!DOCTYPE html PUBLIC "-//W ...
- CDialogEx::OnPaint()的问题,或者为什么在对话框程序的OnPaint中绘图无效的问题
这是一个基于对话框的程序,对话框上有按钮,还有几个CStatic用来绘图,之前都是好好的,今天改成Unicode版本后,编译正常,运行时CStatic中的图像怎么也不显示,有时候会闪现一次就消失,问题 ...
- android之RefBase
路径 system core libutils include utils RefBase.h namespace android 命名空间是android class TextOutput;// 这 ...
- springcloud流程图
自己画的: 别人画的 别人画的2
- python入门 -- 学习笔记4
习题38:列表的操作 当你看到像 mystuff.append('hello') 这样的代码时,你事实上已经在 Python 内部激发了一个连锁反应.以下是它的工作原理: 1. Python 看到你用 ...
- C# 导出dataGridView中的值到Excel
C# 怎么导出dataGridView中的值到Excel 1 2 3 4 5 6 在系统应用过程中,数据是系统的核心.如果直接在应用软件中看数据,有时也有些不便,所以就会把系统数据转换成Excel格式 ...
- java学习笔记(五):公共类
什么是公共类,公共类就是和源文件名同名的类,举例来说:类的名称是 public class aaa{},那么源文件就应该是 aaa.java. 每个源文件中只能有一个公共类. 每个源文件可以有很多非公 ...
- 解题(GeLeiMa -生成格雷码)
题目描述 在一组数的编码中,若任意两个相邻的代码只有一位二进制数不同, 则称这种编码为格雷码(Gray Code),请编写一个函数,使用递归的方法生成N位的格雷码. 给定一个整数n,请返回n位的格雷码 ...
- Yii 框架不同逻辑处理方法统一事务处理
1.定义事务处理接口 <?php namespace frontend\business\SaveRecordByransactions; /** * Interface ISaveForTra ...
- HDU-1260.Tickets(简单线性DP)
本题大意:排队排票,每个人只能自己单独购买或者和后面的人一起购买,给出k个人单独购买和合买所花费的时间,让你计算出k个人总共花费的时间,然后再稍作处理就可得到答案,具体格式看题意. 本题思路:简单dp ...