[JZOJ5837] Omeed

Description

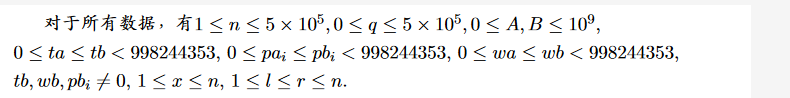
Solution

有两种做法

一种是线段树维护一次方程系数，一种是线段树维护矩阵

准备都写一写

---

维护系数

首先把式子推出来 $$CS=B\times \sum\limits_{i=1}^np_i\times(f_{i-1}+1)$$

\[f_i=(t+p_i-p_i\times t)\times f_{i-1}+p_i
\]

发现 \(f_i\) 是关于 \(f_{i-1}\) 的一次函数 \(y=kx+b\) 形式，可以线段树维护这个 \(k\) 和 \(b\)。

还有 \(p_i\times(f_{i-1}+1)=p_i\times f_{i-1}+p_i\) 也是个一次函数，也能用线段树维护。

具体都维护些什么呢？

在区间 \([L,R]\) 维护 \(k_1,b_1\) 表示 \(f_R=k_1f_{L-1}+b_1\) 和 \(k_2,b_2\) 表示 \(CS[L,R]=k_2f_{L-1}+b_2\)

观察到这样做的好处就是右区间的 \(L-1\) 等于左区间的 \(R\)，这样就资瓷快速合并了。

然后如果一个询问是 \([l,r]\)，那求出来的 \(CS[L,R]\) 的 \(b_2\) 就是答案了。

#include<set>
#include<map>
#include<cmath>
#include<queue>
#include<cctype>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using std::min;
using std::max;
using std::swap;
using std::vector;
typedef double db;
const int N=500005;
typedef long long ll;
const int mod=998244353;
#define pb(A) push_back(A)
#define pii std::pair<int,int>
#define mp(A,B) std::make_pair(A,B)
#define ls cur<<1
#define rs cur<<1|1
#define lss ls,l,mid,ql,qr
#define rss rs,mid+1,r,ql,qr

int n,q,t,tb,A,B,b1[N<<2],b2[N<<2];
int p[N],sump[N<<2],k1[N<<2],k2[N<<2];

struct Node{
    int sump,k1,b1,k2,b2;
    friend Node operator+(Node x,Node y){
        Node z;
        z.sump=(x.sump+y.sump)%mod;
        z.k1=(ll)y.k1*x.k1%mod;
        z.b1=((ll)y.k1*x.b1%mod+y.b1)%mod;
        z.k2=((ll)y.k2*x.k1%mod+x.k2)%mod;
        z.b2=((ll)y.k2*x.b1%mod+y.b2+x.b2)%mod;
        return z;
    }
};

int getint(){
    int X=0,w=0;char ch=0;
    while(!isdigit(ch))w|=ch=='-',ch=getchar();
    while( isdigit(ch))X=X*10+ch-48,ch=getchar();
    if(w) return -X;return X;
}

int ksm(int x,int y){
    int ans=1;
    while(y){
        if(y&1) ans=(ll)ans*x%mod;
        x=(ll)x*x%mod;y>>=1;
    } return ans;
}

int inv(int x){
    return ksm(x,mod-2);
}

void pushup(int cur){
    k1[cur]=(ll)k1[rs]*k1[ls]%mod;
    b1[cur]=((ll)k1[rs]*b1[ls]%mod+b1[rs])%mod;
    k2[cur]=((ll)k2[rs]*k1[ls]%mod+k2[ls])%mod;
    b2[cur]=((ll)k2[rs]*b1[ls]%mod+(ll)b2[rs]+b2[ls])%mod;
    sump[cur]=((ll)sump[ls]+sump[rs])%mod;
}

void build(int cur,int l,int r){
    if(l==r){
        k1[cur]=((ll)t+p[l]-(ll)p[l]*t%mod+mod)%mod;
        b1[cur]=p[l];
        k2[cur]=p[l];
        b2[cur]=p[l];
        sump[cur]=p[l];
        return;
    } int mid=l+r>>1;
    build(ls,l,mid);build(rs,mid+1,r);
    pushup(cur);
}

void modify(int cur,int l,int r,int ql,int qr,int c){
    if(l==r){
        k1[cur]=((ll)t+c-(ll)c*t%mod+mod)%mod;
        b1[cur]=k2[cur]=b2[cur]=sump[cur]=c;
        return;
    } int mid=l+r>>1;
    ql<=mid?modify(lss,c):modify(rss,c);
    pushup(cur);
}

Node query(int cur,int l,int r,int ql,int qr){
    if(ql<=l and r<=qr) return (Node){sump[cur],k1[cur],b1[cur],k2[cur],b2[cur]};
    int mid=l+r>>1;
    if(qr<=mid) return query(lss);
    if(ql>mid) return query(rss);
    return query(lss)+query(rss);
}

signed main(){
    freopen("omeed.in","r",stdin);freopen("omeed.out","w",stdout);
    getint();n=getint(),q=getint(),t=getint(),tb=getint(),A=getint(),B=getint();
    t=(ll)t*inv(tb)%mod;
    for(int i=1;i<=n;i++){
        int x=getint(),y=getint();
        p[i]=(ll)x*inv(y)%mod;
    } build(1,1,n);
    while(q--){
        if(getint()==0){
            int pos=getint(),a=getint(),b=getint(),c=(ll)a*inv(b)%mod;
            p[pos]=c;modify(1,1,n,pos,pos,c);
        } else{
            int l=getint(),r=getint();
            Node ans=query(1,1,n,l,r);
            printf("%d\n",((ll)ans.sump*A%mod+(ll)ans.b2*B%mod)%mod);
        }
    } return 0;
}

---

维护矩阵

上面的DP式子已经列出来了。

我们现在要解决的这样一类问题：我们知道DP式子，现在要求多次从不同的起点开始做DP

求出DP的转移矩阵然后线段树上动态DP就好了

姿势不对会T一个点懒得卡常了

#include<set>
#include<map>
#include<cmath>
#include<queue>
#include<cctype>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using std::min;
using std::max;
using std::swap;
using std::vector;
typedef double db;
const int N=500005;
const int mod=998244353;
typedef long long ll;
#define pb(A) push_back(A)
#define pii std::pair<Mat,int>
#define mp(A,B) std::make_pair(A,B)
#define ls cur<<1
#define rs cur<<1|1
#define lss ls,l,mid,ql,qr
#define rss rs,mid+1,r,ql,qr

int n,q,t,ta,A,B;
int p[N],sum[N<<2];

struct Mat{
    int a[4][4];

    void clear(){
        memset(a,0,sizeof a);
    }

    void init(){
        clear();
        for(int i=1;i<=3;i++) a[i][i]=1;
    }

    friend Mat operator*(Mat x,Mat y){
        Mat z;z.clear();
        for(int i=1;i<=3;i++)
            for(int k=1;k<=3;k++)
                for(int j=1;j<=3;j++)
                    z.a[i][j]=((ll)z.a[i][j]+(ll)x.a[i][k]*y.a[k][j]%mod)%mod;
        return z;
    }
}cs[N<<2];

void pushup(int cur){
    cs[cur]=cs[ls]*cs[rs];
    sum[cur]=(sum[ls]+sum[rs])%mod;
}

void build(int cur,int l,int r){
    if(l==r){
        cs[cur].a[1][1]=((ll)p[l]+t-(ll)p[l]*t%mod+mod)%mod;cs[cur].a[1][2]=(ll)B*p[l]%mod;cs[cur].a[1][3]=0;
        cs[cur].a[2][1]=0;cs[cur].a[2][2]=1;cs[cur].a[2][3]=0;sum[cur]=p[l];
        cs[cur].a[3][1]=p[l];cs[cur].a[3][2]=(ll)p[l]*(B+A)%mod;cs[cur].a[3][3]=1;
        return;
    } int mid=l+r>>1;
    build(ls,l,mid);build(rs,mid+1,r);pushup(cur);
}

void modify(int cur,int l,int r,int ql,int qr,int c){
    if(l==r){
        cs[cur].a[1][1]=((ll)c+t-(ll)c*t%mod+mod)%mod;cs[cur].a[1][2]=(ll)B*c%mod;cs[cur].a[1][3]=0;
        cs[cur].a[2][1]=0;cs[cur].a[2][2]=1;cs[cur].a[2][3]=0;sum[cur]=c;
        cs[cur].a[3][1]=c;cs[cur].a[3][2]=(ll)c*(B+A)%mod;cs[cur].a[3][3]=1;return;
    } int mid=l+r>>1;
    ql<=mid?modify(lss,c):modify(rss,c);
    pushup(cur);
}

Mat query(int cur,int l,int r,int ql,int qr){
    if(ql<=l and r<=qr) return cs[cur];
    int mid=l+r>>1;
    if(qr<=mid) return query(lss);
    if(ql>mid) return query(rss);
    return query(lss)*query(rss);
}

int getint(){
    int X=0,w=0;char ch=0;
    while(!isdigit(ch))w|=ch=='-',ch=getchar();
    while( isdigit(ch))X=X*10+ch-48,ch=getchar();
    if(w) return -X;return X;
}

int ksm(int a,int y){
    int ans=1;
    while(y){
        if(y&1) ans=(ll)ans*a%mod;
        a=(ll)a*a%mod;y>>=1;
    } return ans;
}

int inv(int x){
    return ksm(x,mod-2);
}

signed main(){
    getint(),n=getint(),q=getint(),t=getint(),ta=getint(),A=getint(),B=getint();
    t=(ll)t*inv(ta)%mod;
    for(int i=1;i<=n;i++){
        int x=getint(),y=getint();
        p[i]=(ll)x*inv(y)%mod;
    } build(1,1,n);
    while(q--){
        if(getint()==0){
            int pos=getint(),x=getint(),y=getint(),z=(ll)x*inv(y)%mod;
            modify(1,1,n,pos,pos,z);
        } else{
            int l=getint(),r=getint();
            printf("%d\n",query(1,1,n,l,r).a[3][2]);
        }
    } return 0;
}