PAT A1099 Build A Binary Search Tree （30 分）——二叉搜索树，中序遍历，层序遍历

A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
• Both the left and right subtrees must also be binary search trees.

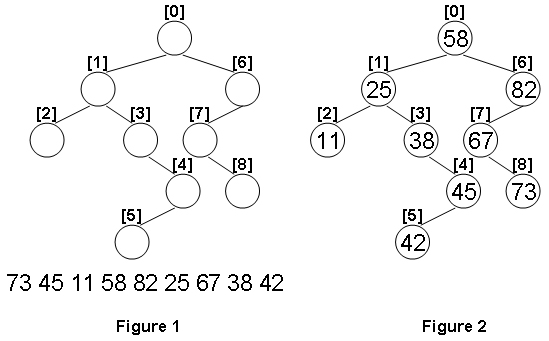
Given the structure of a binary tree and a sequence of distinct integer keys, there is only one way to fill these keys into the tree so that the resulting tree satisfies the definition of a BST. You are supposed to output the level order traversal sequence of that tree. The sample is illustrated by Figure 1 and 2.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤100) which is the total number of nodes in the tree. The next N lines each contains the left and the right children of a node in the format left_index right_index, provided that the nodes are numbered from 0 to N−1, and 0 is always the root. If one child is missing, then −1 will represent the NULL child pointer. Finally N distinct integer keys are given in the last line.

Output Specification:

For each test case, print in one line the level order traversal sequence of that tree. All the numbers must be separated by a space, with no extra space at the end of the line.

Sample Input:

9
1 6
2 3
-1 -1
-1 4
5 -1
-1 -1
7 -1
-1 8
-1 -1
73 45 11 58 82 25 67 38 42

Sample Output:

58 25 82 11 38 67 45 73 42

 #include <stdio.h>
 #include <algorithm>
 #include <set>
 #include <vector>
 #include <queue>
 using namespace std;
 const int maxn = ;
 int n;
 struct node{
     int data;
     int l=-,r=-;
 }bst[maxn];
 int index=;
 int q[maxn];
 void inorder(int root){
     if(bst[root].l!=-) inorder(bst[root].l);
     bst[root].data = q[index++];
     if(bst[root].r!=-) inorder(bst[root].r);
 }
 void level(int root){
     queue<int> que;
     int cnt=;
     que.push(root);
     while(!que.empty()){
         int now=que.front();
         que.pop();
         printf("%d",bst[now].data);
         cnt++;
         if(cnt!=n) printf(" ");
         if(bst[now].l!=-) que.push(bst[now].l);
         if(bst[now].r!=-) que.push(bst[now].r);
     }
 }
 int main(){
     scanf("%d",&n);
     for(int i=;i<n;i++){
         int l,r;
         scanf("%d %d",&l,&r);
         bst[i].l=l;
         bst[i].r=r;
     }
     for(int i=;i<n;i++){
         scanf("%d",&q[i]);
     }
     sort(q,q+n);
     inorder();
     level();
 }

注意点：其实很简单的题目，又一次倒在了递归上。知道要把给定数据sort，但没想sort完后就是这棵树的中序遍历结果，只要把正常中序遍历时的打印改成赋值就能得到那棵树了。没想到中序遍历，所以自己一直在想怎么把这个有序序列一个个填到树里去，一直也没搞明白，看这题通过率0.5多，我还不会做，凉了。

看到树的题目，一般都会要建树，遍历，而对bst，一般都是要对给定序列排序的，这样能得到他的中序遍历结果，有助于建树