洛谷P5206 数树

题意：

task0，给定两棵树T1，T2，取它们公共边(两端点相同)加入一张新的图，记新图连通块个数为x，求y^x。

task1，给定T1，求所有T2的task0之和。

task2，求所有T1的task1之和。

解：y = 1的时候特殊处理，就是总方案数。

task0，显然按照题意模拟即可。

task1，对某个T2，设有k条边相同，那么连通块数就是n - k。要求的就是

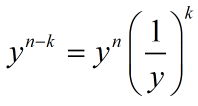
对于每个T2，前面yⁿ都是一样的，所以直接去掉，最后乘上即可。关注后面这个东西怎么求。令y' = 1/y，E是公共边集。

注意到

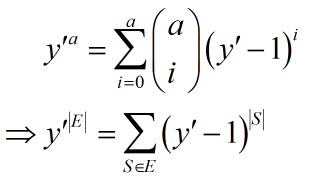
这里下式是枚举边集E的子集S，对每个的子集贡献求和。

注意上式先枚举a再求组合数，相当于枚举在边集里选a条边，然后枚举选哪a条边。也就是枚举子集。

也就是下面这段话想表达的。摘自Cyhlnj。里面还提到了一个n³的矩阵树定理做法，神奇。

容斥写法在下不会T_T

下一步，把S提前枚举，在不同的E中同一个S的贡献总是相同的。考虑一个S会对哪些E产生贡献，也就是它的贡献会被计算多少次。

这|S|条边会形成若干个连通块。这些连通块通过加上一些边可以形成树。这些新边没有任何限制，于是就是连通块的生成树计数。

这里又有若干种推法......个人认为最简单的是利用prufer序列求解。

摘自Joker_69。

令z = y' - 1，m = 边集为S时的连通块数 = n - |S|，第i号连通块有ai个点，于是我们的答案变成了这样：

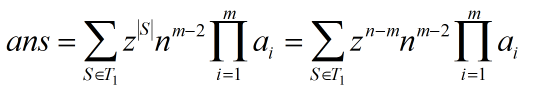
这个东西怎么求呢？注意到在T1中选择任意的边集S等价于把T1划分为若干个连通块，用这些边连起来。于是就考虑树形DP。

这后面这个求积，要乘上每个连通块的大小，有个暴力是f[x][i]表示x为根，x所在连通块大小为i的所有方案权值和。

n²过不了，于是换个思路就是在每个连通块中选一个关键点的方案数。

因为是以联通块为依据DP，所以变形一下，加上之前忽略的yⁿ，我们有：

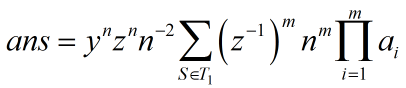
于是状态设计有f[x][0/1]表示在以x为根的子树中，x所在连通块是否选择了关键点的所有方案权值之和。

每个联通块的贡献是z^-1n，且我们只在关键点被选出来的那一瞬间计算这个联通块的贡献。

同时由于每个连通块的贡献要乘起来，那么所有方案之和还是要乘起来，等价于每个方案两两求积再相加。

口胡了半天还是写一下方程吧。

f[x][] = ;
f[x][] = invz * n % MO;

LL t0 = f[x][] * f[y][] % MO + f[x][] * f[y][] % MO;
LL t1 = f[x][] * f[y][] % MO + f[x][] * f[y][] % MO + f[x][] * f[y][] % MO;
f[x][] = t0 % MO;
f[x][] = t1 % MO;

task2：问题变得严重起来......

跟task1一样，对于某个T1和T2的组合，它的贡献仍能拆成它的子集的贡献。

设g(E)为给定E这个边集之后的生成树个数，由task1可得g(E) = n^m-2∏a_i。

枚举E为一定相同的边集，剩下的边随便连。那么对于T1的g(E)种情况，T2都有g(E)种情况。

所以E这个边集的贡献为z^|E|g²(E)。

m还是连通块数，我们暴力展开g(E)，并把与m有关的项放到∏里面，无关的提到外面，令r = n²/z，那么答案就是：

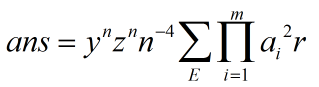
接下来这一步很毒瘤...我们考虑这个式子有什么实际意义。

前面的边集把这个图分成了若干个森林。每个连通块一定是树。后面相当于给每个连通块赋了a_i²r的权值，并把权值乘起来作为这个边集的贡献。

设f_i为大小为i的树的贡献，对应的EGF是F(x)，g_i为大小为i的图的贡献，对应的EGF是G(x)

那么有这样一个式子：G(x) = e^F(x)

考虑f_i是多少：每种树的权值都是i²r，一共有i^i-2种树，贡献加起来是iⁱr。

这样就对F(x)做exp，然后拿G(x)的第n项出来搞一搞就是答案了。

---

多项式操作别写错了......我一开始WA了20分是因为有这样的一句话：n * n

然后两个n乘起来爆int了......这题神奇的一批...

 #include <cstdio>
 #include <algorithm>
 #include <cstring>

 typedef long long LL;
 const int N = ;
 const LL MO = ;

 inline LL qpow(LL a, LL b) {
     LL ans = ;
     a %= MO;
     while(b) {
         if(b & ) ans = ans * a % MO;
         a = a * a % MO;
         b = b >> ;
     }
     return ans;
 }

 struct Edge {
     int nex, v;
 }edge[N << ]; int tp;

 int n, e[N];
 LL Y, z;

 inline void add(int x, int y) {
     tp++;
     edge[tp].v = y;
     edge[tp].nex = e[x];
     e[x] = tp;
     return;
 }

 namespace t0 {
     int fa[N];
     void DFS(int x, int f) {
         fa[x] = f;
         for(int i = e[x]; i; i = edge[i].nex) {
             int y = edge[i].v;
             if(y == f) continue;
             DFS(y, x);
         }
         return;
     }
     inline void solve() {
         if(Y == ) {
             puts("");
             return;
         }
         for(int i = , x, y; i < n; i++) {
             scanf("%d%d", &x, &y);
             add(x, y);
             add(y, x);
         }
         DFS(, );
         int k = ;
         for(int i = , x, y; i < n; i++) {
             scanf("%d%d", &x, &y);
             if(fa[x] == y || fa[y] == x) {
                 k++;
             }
         }
         LL ans = qpow(Y, n - k);
         printf("%lld\n", ans);
         return;
     }
 }

 namespace t1 {
     LL f[N][], invz;
     void DFS(int x, int father) {
         f[x][] = ;
         f[x][] = invz * n % MO;
         //printf("x = %d fa = %d \n", x, father);
         for(int i = e[x]; i; i = edge[i].nex) {
             int y = edge[i].v;
             //printf("y = %d \n", y);
             if(y == father) continue;
             DFS(y, x);
             LL t0 = f[x][] * f[y][] % MO + f[x][] * f[y][] % MO;
             LL t1 = f[x][] * f[y][] % MO + f[x][] * f[y][] % MO + f[x][] * f[y][] % MO;
             f[x][] = t0 % MO;
             f[x][] = t1 % MO;
         }
         //printf("X = %d f[x][0] = %lld f[x][1] = %lld \n", x, f[x][0], f[x][1]);
         return;
     }
     inline void solve() {
         if(Y == ) {
             LL ans = qpow(n, n - );
             printf("%lld\n", ans);
             return;
         }
         z = qpow(Y, MO - ); z = (z -  + MO) % MO;
         invz = qpow(z, MO - );
         for(int i = , x, y; i < n; i++) {
             scanf("%d%d", &x, &y);
             add(x, y); add(y, x);
         }
         DFS(, );
         LL ans = f[][] * qpow(n, MO - ) % MO * qpow(z, n) % MO * qpow(Y, n) % MO;
         printf("%lld\n", ans);
         return;
     }
 }

 namespace t2 {

     typedef LL arr[N * ];
     const LL G = ;

     int r[N * ];
     arr A, B, a, b, inv_t, exp_t, ln_t, ln_t2;
     LL pw[N];

     inline void prework(int n) {
         static int R = ;
         if(R == n) return;
         R = n;
         int lm = ;
         while(( << lm) < n) lm++;
         for(int i = ; i < n; i++) {
             r[i] = (r[i >> ] >> ) | ((i & ) << (lm - ));
         }
         return;
     }

     inline void NTT(LL *a, int n, int f) {
         prework(n);
         for(int i = ; i < n; i++) {
             if(i < r[i]) std::swap(a[i], a[r[i]]);
         }
         for(int len = ; len < n; len <<= ) {
             LL Wn = qpow(G, (MO - ) / (len << ));
             if(f == -) Wn = qpow(Wn, MO - );
             for(int i = ; i < n; i += (len << )) {
                 LL w = ;
                 for(int j = ; j < len; j++) {
                     LL t = a[i + len + j] * w % MO;
                     a[i + len + j] = (a[i + j] - t) % MO;
                     a[i + j] = (a[i + j] + t) % MO;
                     w = w * Wn % MO;
                 }
             }
         }
         if(f == -) {
             LL inv = qpow(n, MO - );
             for(int i = ; i < n; i++) {
                 a[i] = a[i] * inv % MO;
             }
         }
         return;
     }

     void Inv(const LL *a, LL *b, int n) {
         if(n == ) {
             b[] = qpow(a[], MO - );
             b[] = ;
             return;
         }
         Inv(a, b, n >> );
         /// ans = b[i] * (2 - a[i] * b[i])
         memcpy(A, a, n * sizeof(LL)); memset(A + n, , n * sizeof(LL));
         memcpy(B, b, n * sizeof(LL)); memset(B + n, , n * sizeof(LL));
         NTT(A, n << , ); NTT(B, n << , );
         for(int i = ; i < (n << ); i++) b[i] = B[i] * ( - A[i] * B[i] % MO) % MO;
         NTT(b, n << , -);
         memset(b + n, , n * sizeof(LL));
         return;
     }

     inline void getInv(const LL *a, LL *b, int n) {
         int len = ;
         while(len < n) len <<= ;
         memcpy(inv_t, a, n * sizeof(LL)); memset(inv_t + n, , (len - n) * sizeof(LL));
         Inv(inv_t, b, len);
         memset(b + n, , (len - n) * sizeof(LL));
         return;
     }

     inline void der(const LL *a, LL *b, int n) {
         for(int i = ; i < n - ; i++) {
             b[i] = a[i + ] * (i + ) % MO;
         }
         b[n - ] = ;
         return;
     }

     inline void ter(const LL *a, LL *b, int n) {
         for(int i = n - ; i >= ; i--) {
             b[i] = a[i - ] * qpow(i, MO - ) % MO;
         }
         b[] = ;
         return;
     }

     inline void getLn(const LL *a, LL *b, int n) {
         getInv(a, ln_t, n);
         der(a, ln_t2, n);
         int len = ;
         while(len <  * n) len <<= ;
         memset(ln_t + n, , (len - n) * sizeof(LL));
         memset(ln_t2 + n, , (len - n) * sizeof(LL));
         NTT(ln_t, len, ); NTT(ln_t2, len, );
         for(int i = ; i < len; i++) b[i] = ln_t[i] * ln_t2[i] % MO;
         NTT(b, len, -);
         memset(b + n, , (len - n) * sizeof(LL));
         ter(b, b, n);
         return;
     }

     void Exp(const LL *a, LL *b, int n) {
         if(n == ) {
             b[] = ;
             b[] = ;
             return;
         }
         Exp(a, b, n >> );
         /// ans = b * (1 + a - ln b)
         getLn(b, exp_t, n);
         for(int i = ; i < n; i++) A[i] = (a[i] - exp_t[i]) % MO;
         A[] = (A[] + ) % MO;
         memset(A + n, , n * sizeof(LL));
         memcpy(B, b, n * sizeof(LL)); memset(B + n, , n * sizeof(LL));
         NTT(A, n << , ); NTT(B, n << , );
         for(int i = ; i < (n << ); i++) b[i] = A[i] * B[i] % MO;
         NTT(b, n << , -);
         memset(b + n, , n * sizeof(LL));
         return;
     }

     inline void getExp(const LL *a, LL *b, int n) {
         int len = ;
         while(len < n) len <<= ;
         Exp(a, b, len);
         memset(b + n, , (len - n) * sizeof(LL));
         return;
     }

     inline void solve() {
         if(Y == ) {
             LL t = qpow(n, n - );
             printf("%lld\n", t * t % MO);
             return;
         }

         LL z = (qpow(Y, MO - ) - ) % MO;
         LL r = 1ll * n * n % MO * qpow(z, MO - ) % MO;

         pw[] = ;
         for(int i = ; i <= n; i++) {
             pw[i] = pw[i - ] * i % MO;
             a[i] = qpow(i, i) * r % MO * qpow(pw[i], MO - ) % MO;
         }
         getExp(a, b, n + );
         LL ans = b[n] * pw[n] % MO;
         ans = ans * qpow(Y, n) % MO * qpow(z, n) % MO * qpow(n, MO - ) % MO;
         printf("%lld\n", (ans + MO) % MO);
         return;
     }
 }

 int main() {

     int f;
     scanf("%d%lld%d", &n, &Y, &f);
     if(f == ) {
         t0::solve();
         return ;
     }
     if(f == ) {
         t1::solve();
         return ;
     }
     t2::solve();
     return ;
 }

AC代码

以蒟蒻视角写了题解，以后还要继续努力！

感谢：