LDA总结 (一) 共轭分布

今天开始，复习一下 LDA ，记录一些 LDA 的关键步骤，为写好论文做铺垫。第一节的主题是共轭分布，回忆贝叶斯公式：

\[p(\theta|X) = \frac{p(\theta) \cdot p(X|\theta)  }{p(X)} \Leftrightarrow \mathbf{ posterior = \frac{prior \cdot likelihood}{evidence}}\]

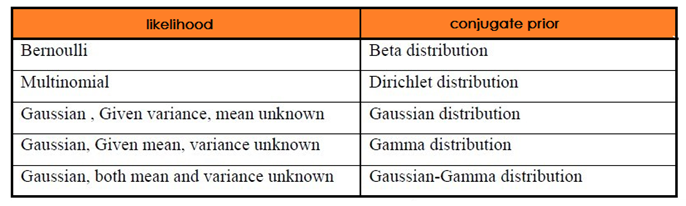
简单来说，如果先验分布 $p(\theta)$ 和似然函数 $p(X|\theta)$ 可以使得先验 $p(\theta)$ 和后验分布 $p(\theta|X)$ 有相同的形式，那么就称先验分布与似然函数是共轭分布。

共轭的意义在于是共轭特性可以使得先验分布和后验分布的形式相同，这样一方面合符人的直观（它们应该是相同形式的）另外一方面是可以形成一个先验链，即现在的后验分布可以作为下一次计算的先验分布，如果形式相同，就可以形成一个链条，后验又可以作为下一次的先验分布。

Binomial 分布

n 次 Binomial 分布试验中事件发生 k 次的概率是：

\[ P(k;n,p) = C_n^k \cdot p^k (1-p)^{n-k} \]

Beta分布

Beta 分布有几个重要的概念，纷纷介绍之：

1. Gamma 函数

\[\Gamma(x) = \int_0^{\infty}t^{x-1}e^{-t}dt\]
它具有如下性质
\[\Gamma(x+1) = x\Gamma(x)\]
2. Beta函数

\[B(m,n) = \frac{\Gamma(m)\Gamma(n)}{\Gamma(m+n)}\]

综上，给出 Beta 分布：

\[f(x) = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha -1}(1-x)^{\beta -1}\]

Multinomial 分布

\[p( \vec n |\vec p ,N) = \frac{N!}{ n_1!n_2!...n_K!} \prod_{k= 1}^K p_k^{n_k}\]

这里有 $n _k$ 代表第 k 个事件发生的计数，且有 $N = n_1 + n_2+…+n_K$.

Dirichlet分布

\[Dir(\vec p|\vec \alpha)=\frac{\Gamma(\sum_{k=1}^K\alpha_k)}{\prod_{k=1}^K\Gamma(\alpha_k)}\prod_{k=1}^Kp_k^{\alpha_k -1}\]
Beta分布和Dirichlet分布的性质

共轭性质

• 当先验为 Beta ，似然为 Binomial分布时，后验仍然为 Beta ，但是这里的 Beta 是融入了 Binomial分布的计数的;
• 当先验为 Dirichlet，似然为 Multinomial 分布时，后验仍然为 Dirichlet，但是这里的 Dirichlet是融入了 Multinomial 分布的计数的.

举例来说，Multinomial  分布中事件 k 发生的次数为 $n_k$ ，则可得一个向量 $ \ vec n $, 代表每个事件的计数，直接使用 Multinomial   的 MLE 得到的结果为：

\[p_k = \frac{n_k}{n_1+n_2+ … +n_K }\]

当对该 Multinomial 分布引入一个 先验为 $\vec {alpha} $ 的 Dirichlet 分布后，即：

\[ p(\vec p) \sim Dir( \vec p| \vec a)\]

采用完全贝叶斯推断的方法，得到该 Dirichlet 分布的后验分布为：

\[Dir(\vec p | \vec a) + Multi(\vec n)= Dir(\vec p | \vec a + \vec n)\]

期望性质

如果 $p \sim Beta(t|\alpha,\beta)$ ,则
\begin{align}E(p)&=\int_0^1 t*Beta(t|\alpha,\beta)dt\\&=\int_0^1 t*\frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)} t^{\alpha-1}(1-t)^{\beta -1}dt\\&=\frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}\int_0^1 t^\alpha(1-t)^{\beta -1}dt\end{align}

上式右边的积分对应到概率分布 $Beta(t|\alpha +1,\beta)$
\[Beta(t | \alpha +1,\beta)=\int_0^1 t*\frac{\Gamma(\alpha + \beta +1 )}{\Gamma(\alpha +1)\Gamma(\beta)} t^\alpha(1-t)^{\beta -1}dt\]
而且我们有
\[\int_0^1Beta(t|\alpha +1,\beta)dt=1\]
所以我们有
\[\int_0^1 t^\alpha(1-t)^{\beta -1}dt=\frac{\Gamma(\alpha+1)\Gamma(\beta)}{\Gamma(\alpha+\beta+1)}\]
把上式带入E(p) 中得到 Beta 分布的期望：
\[E(p)=\frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}\cdot\frac{\Gamma(\alpha+1)\Gamma(\beta)}{\Gamma(\alpha+\beta+1)}=\frac{\alpha}{\alpha + \beta}\]
同样的，对于Dirichlet分布我们可以得到其期望值：
\[E(\vec p)=(\frac{\alpha_1}{\sum_{i=1}{K}\alpha_i},\frac{\alpha_2}{\sum_{i=1}{K}\alpha_i},...,\frac{\alpha_K}{\sum_{i=1}{K}\alpha_i})\]