Edmonds_Karp 算法入门详解(转)

　　转载自：http://blog.csdn.net/hsqlsd/article/details/7862903

　　有n个点，有m条有向边，有一个点很特殊，只出不进，叫做源点，通常规定为1号点。另一个点也很特殊，只进不出，叫做汇点，通常规定为n号点。每条有向边上有两个量，容量和流量，从i到j的容量通常用c[I,j]表示,流量则通常是f[I,j]。通常可以把这些边想象成道路，流量就是这条道路的车流量，容量就是道路可承受的最大的车流量。很显然的，流量<=容量。而对于每个不是源点和汇点的点来说，可以类比的想象成没有存储功能的货物的中转站，所有”进入”他们的流量和等于所有从他本身”出去”的流量。

把源点比作工厂的话，问题就是求从工厂最大可以发出多少货物，是不至于超过道路的容量限制，也就是，最大流。

比如这个图。每条边旁边的数字表示它的容量。

首先，假如所有边上的流量都没有超过容量(不大于容量)，那么就把这一组流量，或者说，这个流，称为一个可行流。一个最简单的例子就是，零流，即所有的流量都是0的流。

我们就从这个零流开始考虑，假如有这么一条路，这条路从源点开始一直一段一段的连到了汇点，并且，这条路上的每一段都满足流量<容量，注意，是严格的<,而不是<=。那么，我们一定能找到这条路上的每一段的(容量-流量)的值当中的最小值delta。我们把这条路上每一段的流量都加上这个delta，一定可以保证这个流依然是可行流，这是显然的。

这样我们就得到了一个更大的流，他的流量是之前的流量+delta，而这条路就叫做增广路。

我们不断地从起点开始寻找增广路，每次都对其进行增广，直到源点和汇点不连通，也就是找不到增广路为止。当找不到增广路的时候，当前的流量就是最大流，这个结论非常重要。

寻找增广路的时候我们可以简单的从源点开始做bfs，并不断修改这条路上的delta量，直到找到源点或者找不到增广路。

这里要先补充一点，在程序实现的时候，我们通常只是用一个c数组来记录容量，而不记录流量，当流量+1的时候，我们可以通过容量-1来实现，以方便程序的实现。

但事实上并没有这么简单，上面所说的增广路还不完整，比如说下面这个网络流模型。

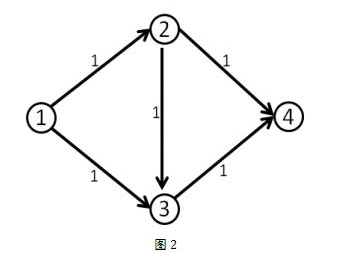
我们第一次找到了1-2-3-4这条增广路，这条路上的delta值显然是1。于是我们修改后得到了下面这个流。（图中的数字是容量）

这时候(1,2)和(3,4)边上的流量都等于容量了，我们再也找不到其他的增广路了，当前的流量是1。

但这个答案明显不是最大流，因为我们可以同时走1-2-4和1-3-4，这样可以得到流量为2的流。

那么我们刚刚的算法问题在哪里呢？问题就在于我们没有给程序一个”后悔”的机会，应该有一个不走(2-3-4)而改走(2-4)的机制。那么如何解决这个问题呢？回溯搜索吗？那么我们的效率就上升到指数级了。

而这个算法神奇的利用了一个叫做反向边的概念来解决这个问题。即每条边(I,j)都有一条反向边(j,i)，反向边也同样有它的容量。

我们直接来看它是如何解决的：

在第一次找到增广路之后，在把路上每一段的容量减少delta的同时，也把每一段上的反方向的容量增加delta。即在Dec(c[x,y],delta)的同时，inc(c[y,x],delta)

我们来看刚才的例子，在找到1-2-3-4这条增广路之后，把容量修改成如下

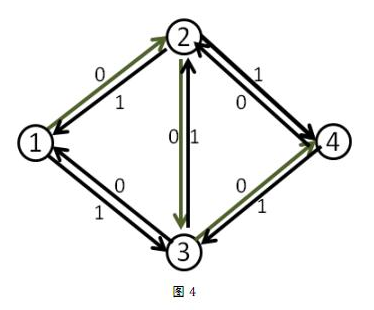
这时再找增广路的时候，就会找到1-3-2-4这条可增广量，即delta值为1的可增广路。将这条路增广之后，得到了最大流2。

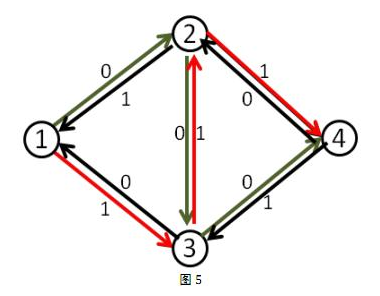
那么，这么做为什么会是对的呢？

事实上，当我们第二次的增广路走3-2这条反向边的时候，就相当于把2-3这条正向边已经是用了的流量给”退”了回去，不走2-3这条路，而改走从2点出发的其他的路也就是2-4。（有人问如果这里没有2-4怎么办，这时假如没有2-4这条路的话，最终这条增广路也不会存在，因为他根本不能走到汇点）同时本来在3-4上的流量由1-3-4这条路来”接管”。而最终2-3这条路正向流量1，反向流量1，等于没有流量。

这就是这个算法的精华部分，利用反向边，使程序有了一个后悔和改正的机会。

附Edmonds_Karp算法模板

#define maxn 220
#define INF 0x7f7f7f7f
int cap[maxn][maxn],flow[maxn][maxn];
int pre[maxn],res[maxn];//res[i] 残量
int Edmonds_Karp(int start,int end)
{
    int maxflow=;
    memset(flow,,sizeof(flow));
    memset(pre,,sizeof(pre));
    queue<int> q;
    while(true)
    {
        memset(res,,sizeof(res));
        res[start]=INF;
        q.push(start);
        while(!q.empty()) //BFS寻找增广路
        {
            int u=q.front();
            q.pop();
            for(int v=;v<=end;v++)
                if(!res[v]&&cap[u][v]>flow[u][v])
                {
                    res[v]=min(res[u],cap[u][v]-flow[u][v]);//start-v路径上的最小残量
                    //记录v的父亲，并加入队列中
                    pre[v]=u;
                    q.push(v);
                }
        }
        if(res[end]==) return maxflow;//无法继续更新最大流量，则当前流已经是最大流
        for(int u=end;u!=start;u=pre[u])//从汇点往回走
        {
            flow[pre[u]][u]+=res[end];//更新正向流
            flow[u][pre[u]]-=res[end];//更新反向流
        }
        maxflow+=res[end]; //更新从s流出的总流量
    }
}
int main()
{
    //
    memset(cap,,sizeof(cap));
    //
    for(/**/)
    {
        int u,v,s;
        scanf("%d %d %d",&u,&v,&s);
        cap[u][v]+=s;//要考虑到重边问题
    }
    //
    return ；
}