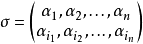[HNOI2008]Cards(dp,Burnside引理)
Burnside引理:
相关概念
- 群:在数学中,群表示一个拥有满足封闭性、满足结合律、有单位元、有逆元的二元运算的代数结构。
置换群:由有限集合各元素的置换所构成的群。
一个置换的形式类似于
然后是Burnside引理:
(1)玄学描述
在一个置换群G={a1,a2,a3……ak}中,把每个置换都写成不相交循环的乘积。
设C1(ak)是在置换ak的作用下不动点的个数,也就是长度为1的循环的个数。
通过上述置换的变换操作后可以相等的元素属于同一个等价类
那么等价类的个数就等于:
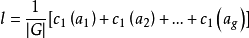
即置换群中每个置换的不动点的平均数
(2)对公式的理解
eg:一正方形分成4格,2着色,有多少种方案?其中,经过转动相同的图象算同一方案。
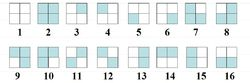
关于转动,一共有四种置换方法,也就是|G|=4
不动(360度):a1=(1)(2)…(16)
逆时针转90度 :a2=(1)(2)(3 4 5 6)(7 8 9 10) (11 12)(13 14 15 16)
顺时针转90度 :a3=(1)(2)(6 5 4 3)(10 9 8 7)(11 12)(16 15 14 13)
转180度:a4=(1)(2)(3 5)(4 6)(7 9)(8 10)(11)(12) (13 15)(14 16)
对括号的理解: 假设转动方式(不动、逆时针转90度、顺时针转90度、转180度)为运算符+。 则+表示逆时针转90度时,括号(3 4 5 6)表示(3+4+5+6+)为一个循环,即(3+4+5+6+)=3(回到原点);
然后我们针对每一种置换的方式,找到其中的不动点,也就是只有自己的情况
由Burnside引理,共有(16+2+2+4)/4=6(种方案)
Polya定理
再提一提那个我不懂的Polya定理吧(哪天懂了回来解释)
国家集训队2001论文集 符文杰 Polya原理及其应用
Polya定理实际上是Burnside引理的具体化,提供了计算不动点的具体方法:
- 假设一个置换有σk">σk个循环,就是轮换
- 易知每个循环对应的所有位置颜色需一致,而任意两个循环之间选什么颜色互不影响。
- 因此,如果有m种可选颜色,则该置换对应的不动点个数为mσk">m^σk。
- 用其替换Burnside引理中的C(G)">C(G),即C(G)=mk">C(G)=m^k。得到等价类数目为:
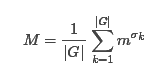

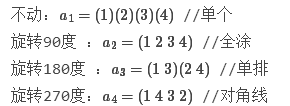
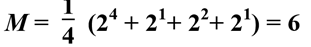
现在借这道题学会运用Burnside引理
- Description
题目描述
小春现在很清闲,面对书桌上的N张牌,他决定给每张染色,目前小春只有3种颜色:红色,蓝色,绿色.他询问Sun有多少种染色方案,Sun很快就给出了答案.
进一步,小春要求染出Sr张红色,Sb张蓝色,Sg张绿色.他又询问有多少种方案,Sun想了一下,又给出了正确答案. 最后小春发明了M种不同的洗牌法,这里他又问Sun有多少种不同的染色方案.两种染色方法相同当且仅当其中一种可以通过任意的洗牌法(即可以使用多种洗牌法,而每种方法可以使用多次)洗成另一种.
Sun发现这个问题有点难度,决定交给你,答案可能很大,只要求出答案除以P的余数(P为质数).
输入格式
第一行输入 5 个整数:Sr,Sb,Sg,m,p(m<=60,m+1<p<100)。n=Sr+Sb+Sg。接下来 m 行,每行描述一种洗牌法,每行有 n 个用空格隔开的整数 X1X2...Xn,恰为 1 到 n 的一个排列,表示使用这种洗牌法,第 i位变为原来的 Xi位的牌。输入数据保证任意多次洗牌都可用这 m种洗牌法中的一种代替,且对每种
洗牌法,都存在一种洗牌法使得能回到原状态。
100%数据满足 Max{Sr,Sb,Sg}<=20。
输出格式
不同染法除以P的余数
- Solution
运用01背包求出每一种置换(注意不动也是一种置换)的不动点个数,再运用Burnside引理求出等价类个数
- Code
- #include <cstdio>
- #include <cstdlib>
- #include <cstring>
- #define ll long long
- using namespace std;
- int s1,s2,s3,m,a[][],size[],tot,n;
- ll p,f[][][],ans;
- bool vis[];
- ll ksm(ll a,int b)//快速幂求逆元
- {
- ll x=a,ans=;
- while(b)
- {
- if(b&) ans=(ans*x)%p;
- x=(x*x)%p,b>>=;
- }
- return ans;
- }
- ll Dp(int x)//01背包
- {
- memset(vis,false,sizeof(vis));
- memset(f,,sizeof(f));
- tot=;
- for(int i=;i<=n;i++)
- if(!vis[i])
- {
- vis[i]=true,size[++tot]=;
- int p=i;
- while(!vis[a[x][p]]) vis[p=a[x][p]]=true,size[tot]++;
- }
- f[][][]=;
- for(int i=;i<=tot;i++)
- for(int j1=s1;j1>=;j1--)
- for(int j2=s2;j2>=;j2--)
- for(int j3=s3;j3>=;j3--)
- {
- if(j1>=size[i]) f[j1][j2][j3]=(f[j1][j2][j3]+f[j1-size[i]][j2][j3])%p;
- if(j2>=size[i]) f[j1][j2][j3]=(f[j1][j2][j3]+f[j1][j2-size[i]][j3])%p;
- if(j3>=size[i]) f[j1][j2][j3]=(f[j1][j2][j3]+f[j1][j2][j3-size[i]])%p;
- }
- return f[s1][s2][s3];
- }
- int main()
- {
- scanf("%d%d%d%d%lld",&s1,&s2,&s3,&m,&p);
- n=s1+s2+s3;
- for(int i=;i<=m;i++)
- for(int j=;j<=n;j++)
- scanf("%d",&a[i][j]);
- m++;
- for(int i=;i<=n;i++) a[m][i]=i;
- for(int i=;i<=m;i++)
- ans=(ans+Dp(i))%p;//Burnside引理
- printf("%lld\n",ans*ksm((long long)m,p-)%p);
- return ;
- }
[HNOI2008]Cards(dp,Burnside引理)的更多相关文章
- BZOJ 1004: [HNOI2008]Cards( 置换群 + burnside引理 + 背包dp + 乘法逆元 )
题意保证了是一个置换群. 根据burnside引理, 答案为Σc(f) / (M+1). c(f)表示置换f的不动点数, 而题目限制了颜色的数量, 所以还得满足题目, 用背包dp来计算.dp(x,i, ...
- [BZOJ 1004] [HNOI2008] Cards 【Burnside引理 + DP】
题目链接:BZOJ - 1004 题目分析 首先,几个定义和定理引理: 群:G是一个集合,*是定义在这个集合上的一个运算. 如果满足以下性质,那么(G, *)是一个群. 1)封闭性,对于任意 a, b ...
- [bzoj1004][HNOI2008][Cards] (置换群+Burnside引理+动态规划)
Description 小春现在很清闲,面对书桌上的N张牌,他决定给每张染色,目前小春只有3种颜色:红色,蓝色,绿色.他询问Sun有多少种染色方案,Sun很快就给出了答案.进一步,小春要求染出Sr张红 ...
- BZOJ 1004 Cards(Burnside引理+DP)
题目链接:http://61.187.179.132/JudgeOnline/problem.php?id=1004 题意:三种颜色的扑克牌各有Sr,Sb,Sg张.给出m种置换.两种染色方案在某种置换 ...
- [bzoj 1004][HNOI 2008]Cards(Burnside引理+DP)
题目:http://www.lydsy.com/JudgeOnline/problem.php?id=1004 分析: 1.确定方向:肯定是组合数学问题,不是Polya就是Burnside,然后题目上 ...
- BZOJ_[HNOI2008]_Cards_(置换+Burnside引理+乘法逆元+费马小定理+快速幂)
描述 http://www.lydsy.com/JudgeOnline/problem.php?id=1004 共n个卡片,染成r,b,g三种颜色,每种颜色的个数有规定.给出一些置换,可以由置换得到的 ...
- BZOJ1004 [HNOI2008]Cards 【burnside定理 + 01背包】
题目链接 BZOJ1004 题解 burnside定理 在\(m\)个置换下本质不同的染色方案数,等于每种置换下不变的方案数的平均数 记\(L\)为本质不同的染色方案数,\(m\)为置换数,\(f(i ...
- bzoj1004 [HNOI2008]Cards【Burnside/Polya】
传送门:http://www.lydsy.com/JudgeOnline/problem.php?id=1004 一道好题,但并不是好在融合了三个“考点”(计数,背包dp,逆元),其实背包dp以及求逆 ...
- 【BZOJ1004】【HNOI2008】Cards 群论 置换 burnside引理 背包DP
题目描述 有\(n\)张卡牌,要求你给这些卡牌染上RGB三种颜色,\(r\)张红色,\(g\)张绿色,\(b\)张蓝色. 还有\(m\)种洗牌方法,每种洗牌方法是一种置换.保证任意多次洗牌都可用这\( ...
随机推荐
- CentOS7.6部署k8s环境
CentOS7.6部署k8s环境 测试环境: 节点名称 节点IP 节点功能 K8s-master 10.10.1.10/24 Master.etcd.registry K8s-node-1 10.10 ...
- C++引用计数设计与分析(解决垃圾回收问题)
1.引言 上一篇博文讲到https://www.cnblogs.com/zhaoyixiang/p/12116203.html 我们了解到我们在浅拷贝时对带指针的对象进行拷贝会出现内存泄漏,那C++是 ...
- Redisson实现Redis分布式锁的底层原理
一.写在前面 现在面试,一般都会聊聊分布式系统这块的东西.通常面试官都会从服务框架(Spring Cloud.Dubbo)聊起,一路聊到分布式事务.分布式锁.ZooKeeper等知识.所以咱们这篇文章 ...
- jitamin基于lnmp环境搭建
从github上面下载源代码 cd /Data/apps/nginx/html git clone https://github.com/jitamin/jitamin.git 修改配置文件 cd ...
- Python基础(二):操作基本数据类型
Python是一门解释型语言,它的优势在于代码简洁,易于理解,可以通过大量已封装好的内建方法和第三方模块方法完成日常所需的操作. 字符串 索引 起始下标为0 (从前往后数),末尾下标为-1(从后往前数 ...
- Swift之代码混淆的调研实施小记
背景: 最近做APP备案,需要对项目做一系列对优化改进,其中就包括了代码混淆,顾名思义,混淆是为了代码安全,是为了增加逆向破解的难度与复杂度. 目前市面上,免费和付费都有,一些公司对APP加固已经做成 ...
- linux下压缩包的解压
linux下 最常见的是 .tar.gz 包和.tar.bz2包 .tar.gz格式的压缩包解压命令是: tar -zxvf xx.tar.gz .tar.bz2格式的压缩包 ...
- 《C++Primer》第五版习题答案--第二章【学习笔记】
C++Primer第五版习题解答---第二章 ps:答案是个人在学习过程中书写,可能存在错漏之处,仅作参考. 作者:cosefy Date: 2020/1/9 第二章:变量和基本类型 练习2.1: 类 ...
- java小项目之:象棋,羡慕你们有对象的!
象棋,是我国传统棋类益智游戏,在中国有着悠久的历史,属于二人对抗性游戏的一种,由于用具简单,趣味性强,成为流行极为广泛的棋艺活动.中国象棋是中国棋文化也是中华民族的文化瑰宝. 象棋还有很多口诀,这是最 ...
- Django之Session与Cookie
目录 一.cookie Cookie的由来 什么是Cookie Cookie的原理 查看Cookie cookie与session的作用 二.Django中操作Cookie 获取Cookie 设置Co ...