b 解题报告

本题已收录至2019/9/15 本周总结

题目

【问题描述】

Hja有一棵\(n\)个点的树,树上每个点有点权,每条边有颜色.一条路径的权值是这条路径上所有点的点权和,一条合法的路径需要满足该路径上任意相邻的两条边颜色都不相同.问这棵树上所有合法路径的权值和是多少.

【输入格式】

第一行一个数\(n\).

接下来一行\(n\)个数代表每个点的权值.

接下来\(n-1\)行每行三个整数\(u\ v\ c\)，代表\(u\)到\(v\)之间有一条颜色为\(c\)的边。

【输出格式】

一行一个整数代表答案.

【样例输入】

6
6 2 3 7 1 4
1 2 1
1 3 2
1 4 3
2 5 1
2 6 2

【样例输出】

134

【数据范围与规定】

\(1\le n \le 3\times 10^5,1\le c \le 10^9\)

保证答案小于\(2^{63}-1\).

思路1 \(O(n^2)\)暴力

从每个点DFS一次,计算出以该点为端点的所有合法路径的权值和.每条链被计算了两次,因此答案要\(/2\).

时间复杂度\(O(n^2)\)

#include<bits/stdc++.h>
#define LL long long
const int SIZE=300005;
int n,head[SIZE],nex[SIZE*2],to[SIZE*2],edge[SIZE*2],Tot;
LL weight[SIZE],Ans;

void Link(int u,int v,int e)
{
	nex[++Tot]=head[u];head[u]=Tot;to[Tot]=v;edge[Tot]=e;
	nex[++Tot]=head[v];head[v]=Tot;to[Tot]=u;edge[Tot]=e;
}

void DFS(int u,int F,LL sum,int Las)
{
	Ans+=sum;
	for(int i=head[u];i;i=nex[i])
	{
		int v=to[i];
		if(v==F||edge[i]==Las)continue;//不能出现连续两条颜色相同的边
		DFS(v,u,sum+weight[v],edge[i]);
	}
}

int main()
{
	int u,v,e;
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%lld",&weight[i]);
		Ans-=weight[i];
	}
	for(int i=1;i<n;i++)
	{
		scanf("%d%d%d",&u,&v,&e);
		Link(u,v,e);
	}
	for(int i=1;i<=n;i++)DFS(i,0,weight[i],0);
	printf("%lld",Ans/2);
	return 0;
}

思路2 \(O(n^2)\)记忆化搜索

容易发现,思路1的搜索有大量的重复状态.

举个例子,

现在我们从涂黑的点开始搜索,在粉框里搜出来了4种状态,列举在了右边.

需要注意的是,有一种状态(粉框左下角的连续两条蓝边)是不合法的,我们没有保留这种状态.

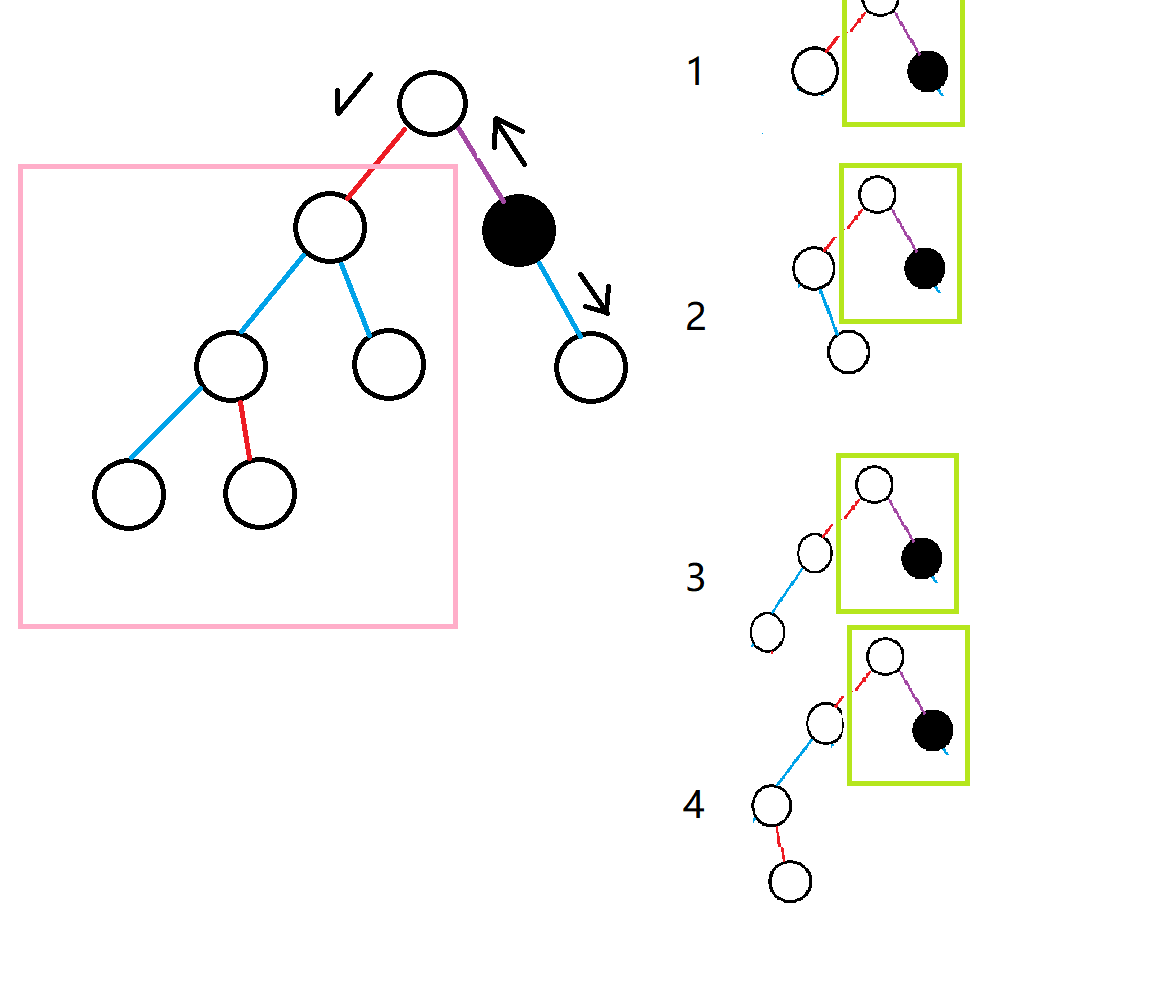
现在我们换第二个点进行DFS,就拿上图中涂黑的点来举例吧.

从这个点开始搜索,依然会进入粉框,在粉框中依然会搜出这4种状态,列举在了右边.

容易发现,这4种状态和上一个点的状态基本一样,只有绿框中的不一样.

换句话说,这4种状态在粉框中的部分是一样的.

这启示我们把粉框里搜出来的状态存起来,下次直接调用,不再在粉框内部进行DFS.

也就是这样:

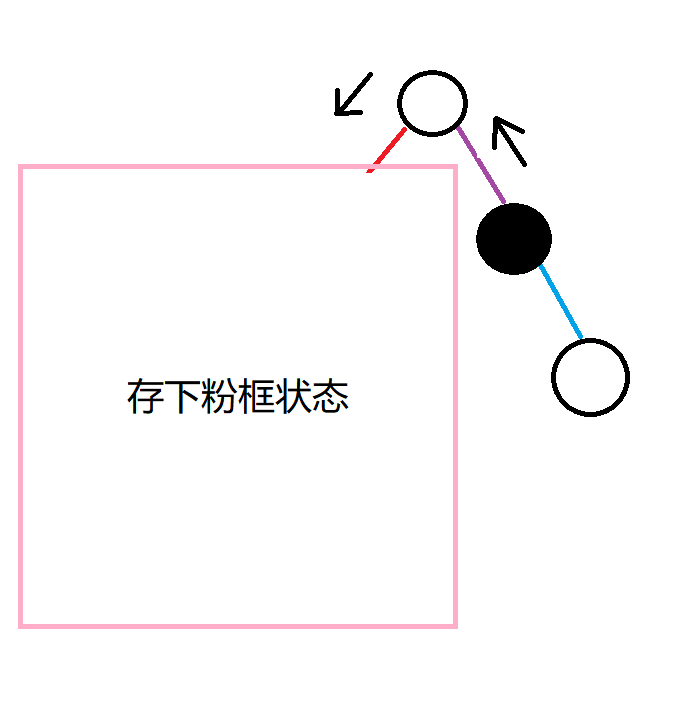
当我们在搜涂黑的点时,不用进入粉框搜索了,直接取出粉框的状态,加入答案.

容易发现,状态应该存储在(有向)边上,而且这样的记忆化可以推广到所有边.

于是我们就得到了记忆化搜索的代码.

#include<bits/stdc++.h>
#define LL long long
const int SIZE=600005;
int n,head[SIZE],nex[SIZE],to[SIZE],edge[SIZE],Tot;
LL weight[SIZE],Ans;

void Link(int u,int v,int e)
{
	nex[++Tot]=head[u];head[u]=Tot;to[Tot]=v;edge[Tot]=e;
	nex[++Tot]=head[v];head[v]=Tot;to[Tot]=u;edge[Tot]=e;
}

struct Re
{
	LL Res;
	int w;
	Re operator +(const Re &o)const
	{
		return (Re){Res+o.Res,w+o.w};
	}
}x[SIZE];
Re DFS(int u,int F,LL sum,int Las)
{
	Re R=(Re){sum,1};
	for(int i=head[u];i;i=nex[i])
	{
		int v=to[i];
		if(v==F||edge[i]==Las)continue;
		if(x[i].w)R=(Re){R.Res+x[i].w*sum+x[i].Res,R.w+x[i].w};
		else
		{
			Re Tem=DFS(v,u,sum+weight[v],edge[i]);
			R=R+Tem;
			x[i]=(Re){Tem.Res-sum*Tem.w,Tem.w};
		}
	}
	return R;
}

int main()
{
	int u,v,e;
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%lld",&weight[i]);
		Ans-=weight[i];
	}
	for(int i=1;i<n;i++)
	{
		scanf("%d%d%d",&u,&v,&e);
		Link(u,v,e);
	}
	for(int i=1;i<=n;i++)
		Ans+=DFS(i,0,weight[i],0).Res;
	printf("%lld",Ans/2);
	return 0;
}

容易证明:

一条链的情况时间复杂度\(O(n)\).

随机数据时间复杂度近似\(O(n)\).

菊花图时间复杂度\(O(n^2)\)

证明略.

思路3 记忆化搜索的优化

刚刚睡觉的时候想到可以对点也记忆化,但是这样要用map,时间复杂度\(O(nlogn)\).

#include<bits/stdc++.h>
#define LL long long
const int SIZE=600005;
int n,head[SIZE],nex[SIZE],to[SIZE],edge[SIZE],Tot;
LL weight[SIZE],Ans;

void Link(int u,int v,int e)
{
    nex[++Tot]=head[u];head[u]=Tot;to[Tot]=v;edge[Tot]=e;
    nex[++Tot]=head[v];head[v]=Tot;to[Tot]=u;edge[Tot]=e;
}

struct Re
{
    LL Res;int w;
    Re operator +(const Re &o)const{return (Re){Res+o.Res,w+o.w};}
    Re operator -(const Re &o)const{return (Re){Res-o.Res,w-o.w};}
}x[SIZE],mk[SIZE];
std::map<std::pair<int,int>,Re>mp;

bool Finished[SIZE];
Re DFS(int u,int F,LL sum,int Las)
{
    Re R=(Re){sum,1};
    if(Finished[u])
    {
    	Re Tem=mk[u]-mp[std::make_pair(u,Las)];
		R=(Re){R.Res+Tem.w*sum+Tem.Res,R.w+Tem.w};
		return R;
	}
    for(int i=head[u];i;i=nex[i])
    {
        int v=to[i];
        if(v==F){if(x[i].w)Finished[u]=1;continue;}
        if(x[i].w)
		{
			if(edge[i]!=Las)R=(Re){R.Res+x[i].w*sum+x[i].Res,R.w+x[i].w};
			continue;
		}
        Re Tem=DFS(v,u,sum+weight[v],edge[i]);
        if(edge[i]!=Las)R=R+Tem;
        x[i]=(Re){Tem.Res-sum*Tem.w,Tem.w};
        mp[std::make_pair(u,edge[i])]=mp[std::make_pair(u,edge[i])]+x[i];
        mk[u]=mk[u]+x[i];
    }
    return R;
}

int main()
{
    int u,v,e;
    scanf("%d",&n);
    for(int i=1;i<=n;++i){scanf("%lld",&weight[i]);Ans-=weight[i];}
    for(int i=1;i<n;++i){scanf("%d%d%d",&u,&v,&e);Link(u,v,e);}
    for(int i=1;i<=n;++i)Ans+=DFS(i,0,weight[i],0).Res;
    printf("%lld",Ans/2);
    return 0;
}